 @GeoffreyDeSmet
@GeoffreyDeSmet
Presentation instructions
- Press the page down key to go to the first real slide
- Press the escape key for an overview of all slides
Tips:
- Do an OptaPlanner presentation and reuse some of these slides
- Click here to hide the instructions and controls
- Print to PDF (Google Chrome recommended)
- ODP/PPT/PPTX: Open the PDF in LibreOffice and copy the slides into a new ODP/PPT/PPTX file

Do more business
with less resources
by Geoffrey De Smet
OptaPlanner lead
Traveling Salesman Problem
(TSP)
&
Vehicle Routing Problem
(VRP)
Press down to show
Press right to skip
The story
of
the ultimate American road trip
https://www.washingtonpost.com/news/wonk/wp/2015/03/10/a-data-genius-computes-the-ultimate-american-road-trip/
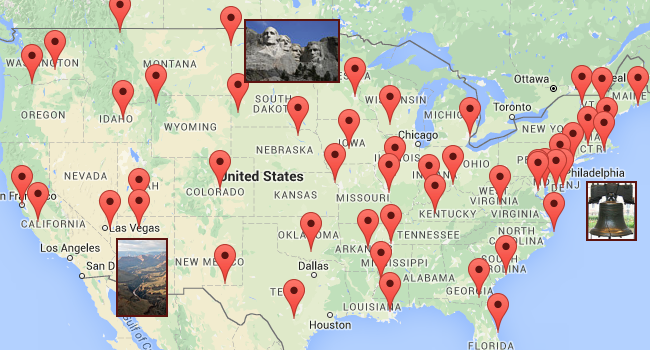
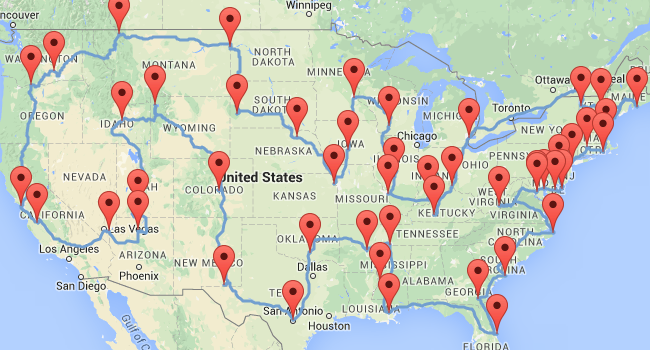
Road trip for 50 landmarks, monuments, etc.
Traditional algorithm: 271h 35m 16s
Is it optimal?
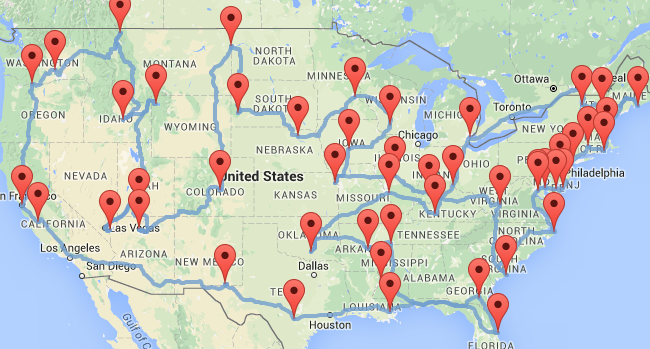
Olson's trip: 232h 43m 10s
⇒ 38h 52m 6s faster (14%)
Is it optimal?
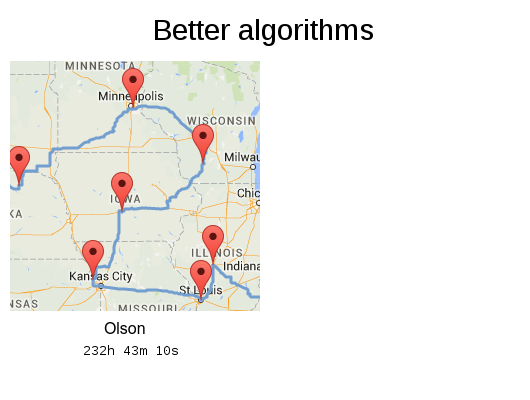
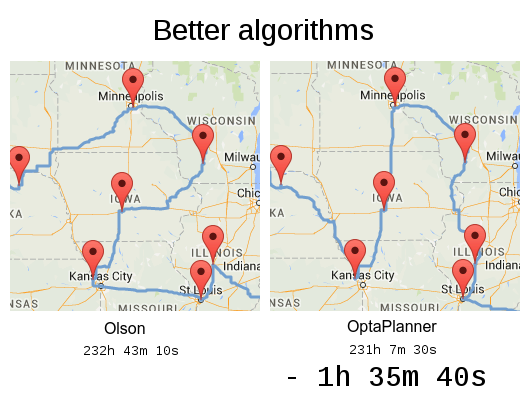
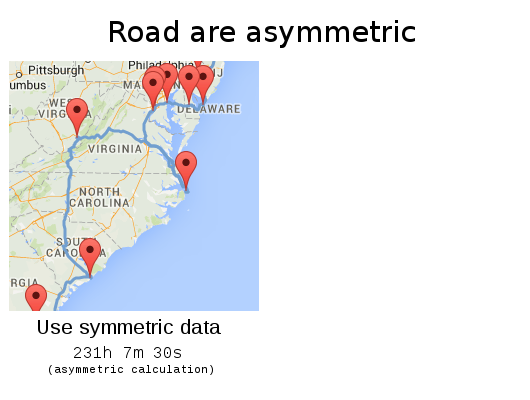
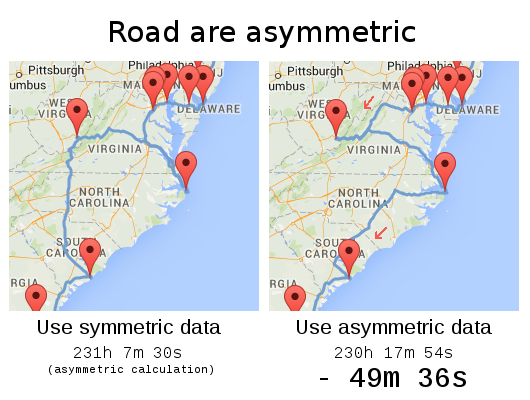

Olson's trip: 232h 43m 10s
Not optimal
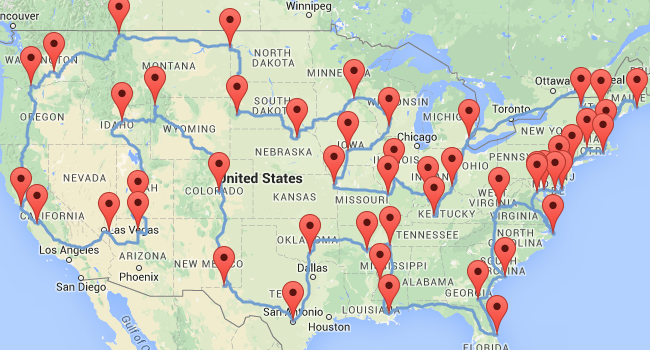
OptaPlanner's trip: 230h 17m 54s
⇒ Another 2h 25m 16s faster (1% ⇒ 15% in total)
Optimal, also 33km 710m (= 20.95 miles) shorter
What is constraint solving?
TSP demo
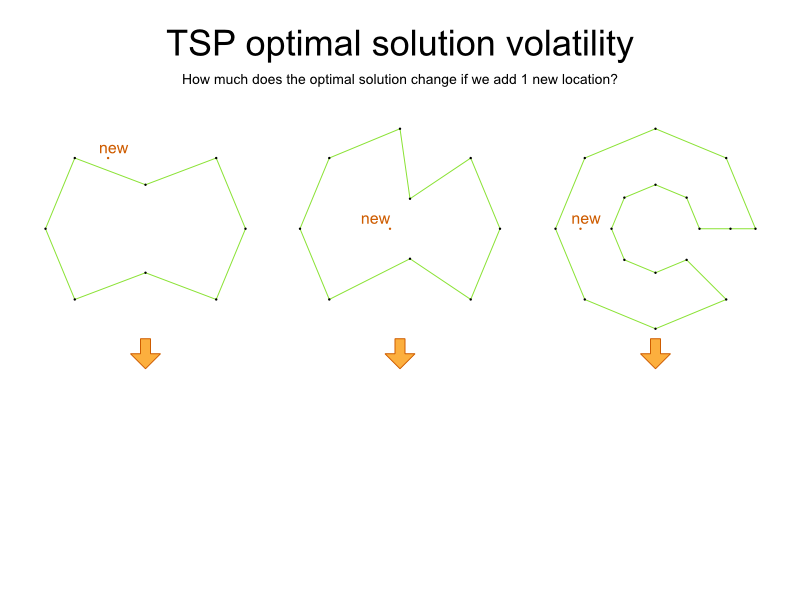
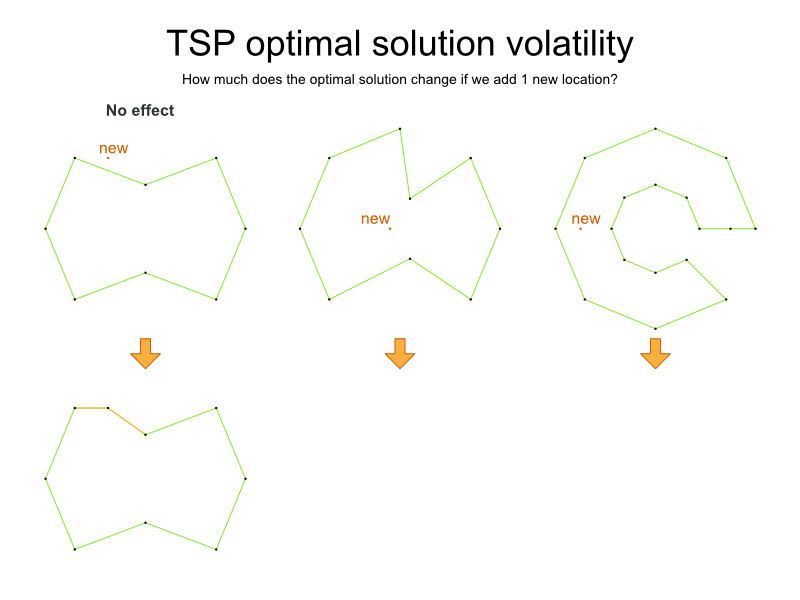
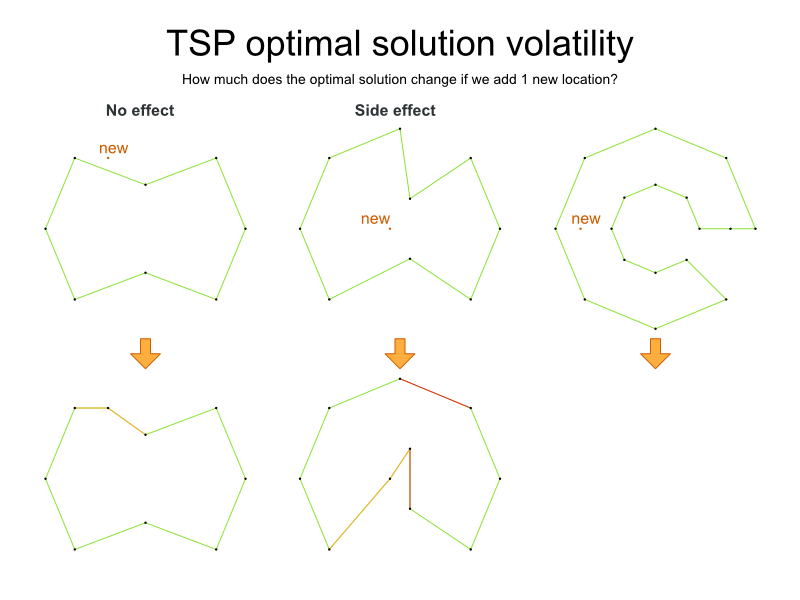
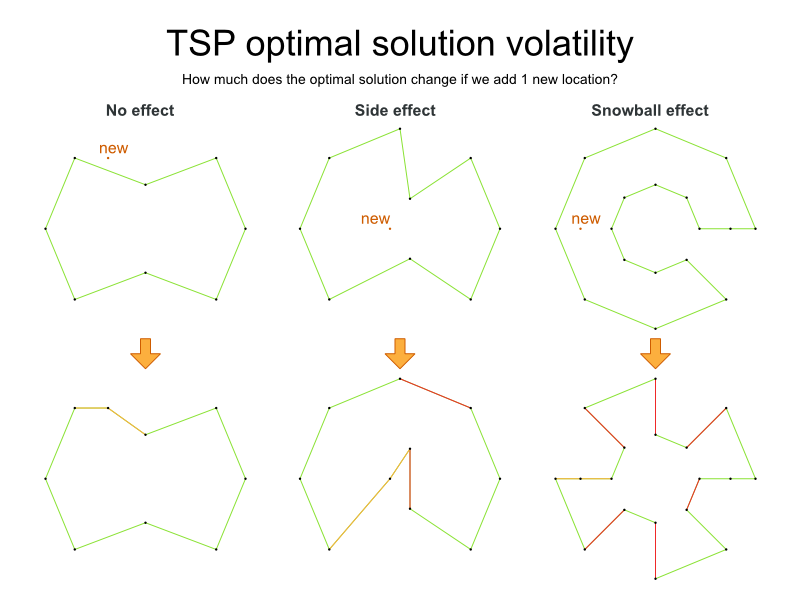

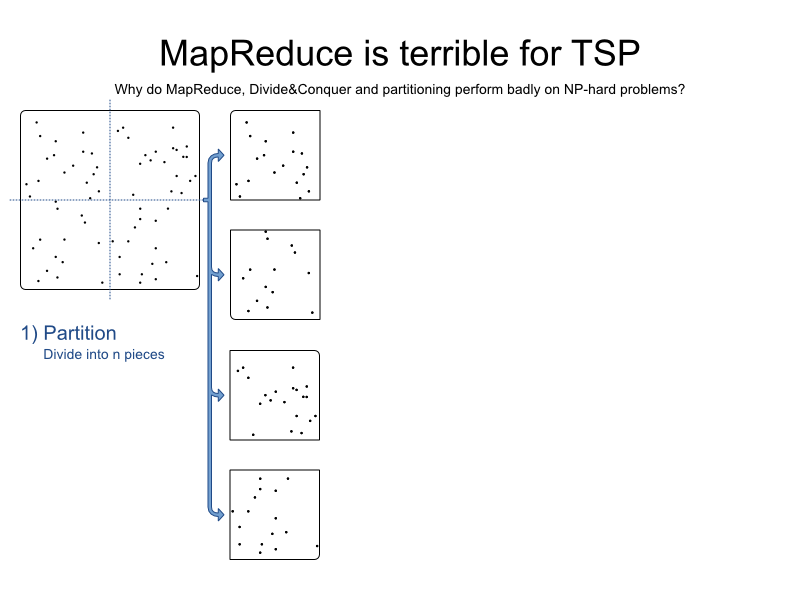
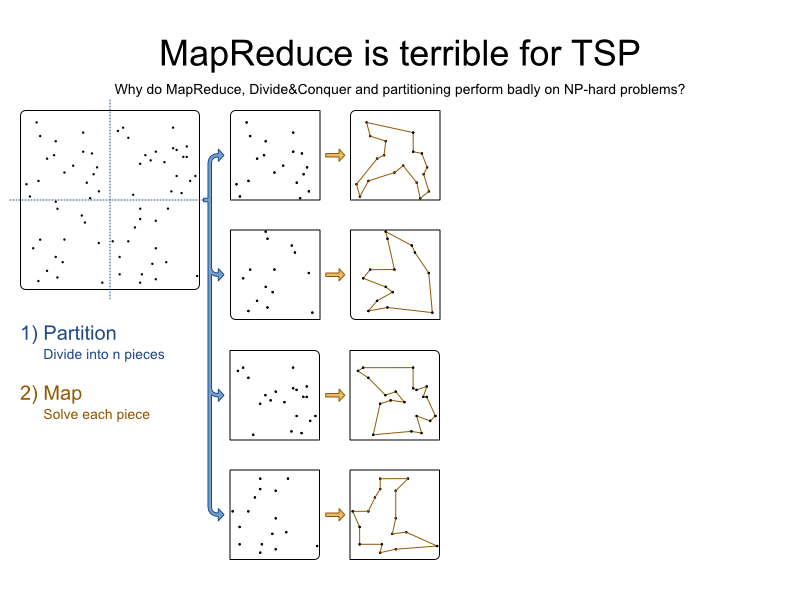
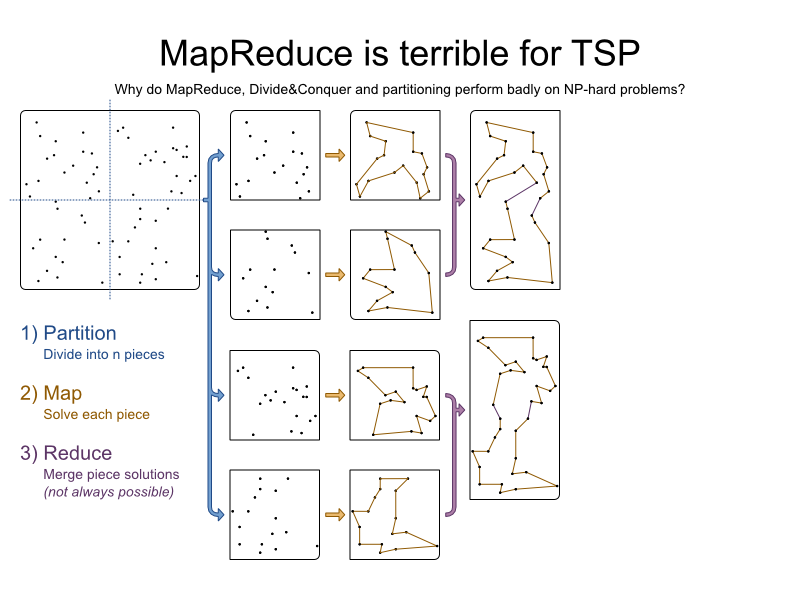
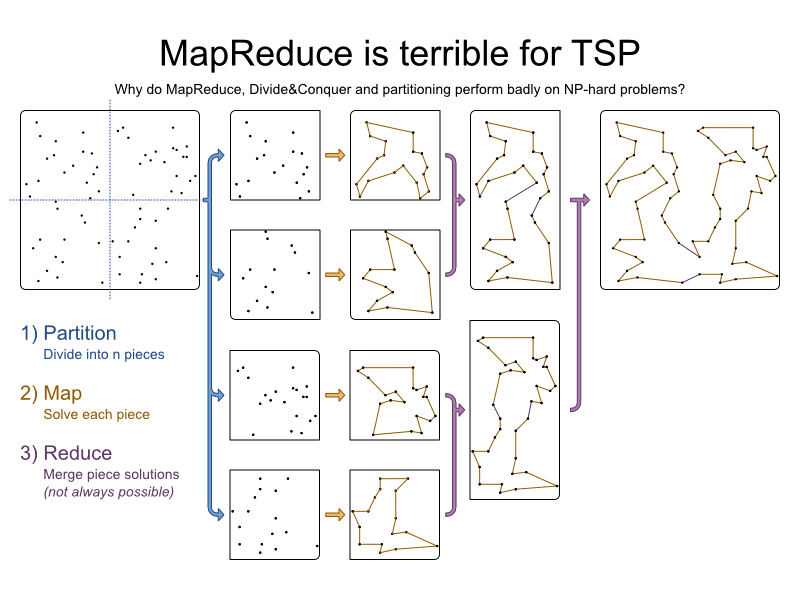
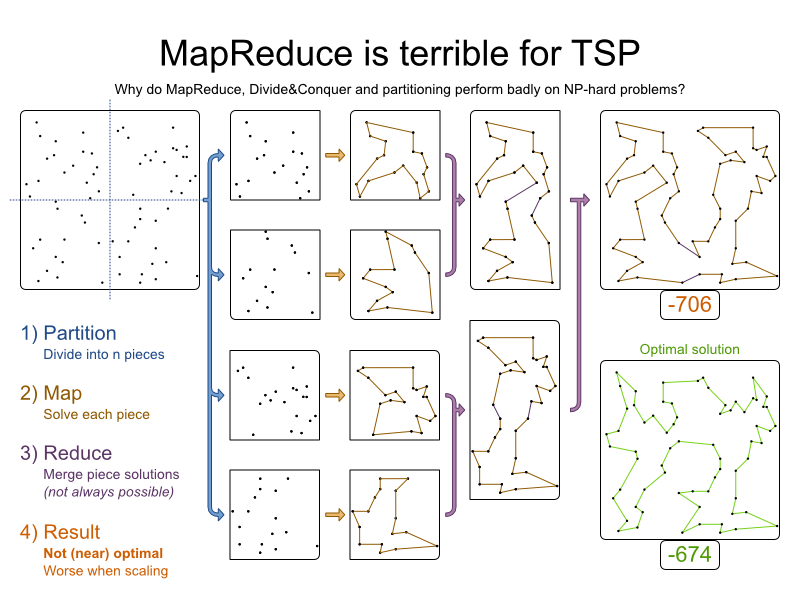
TSP
is an academic problem
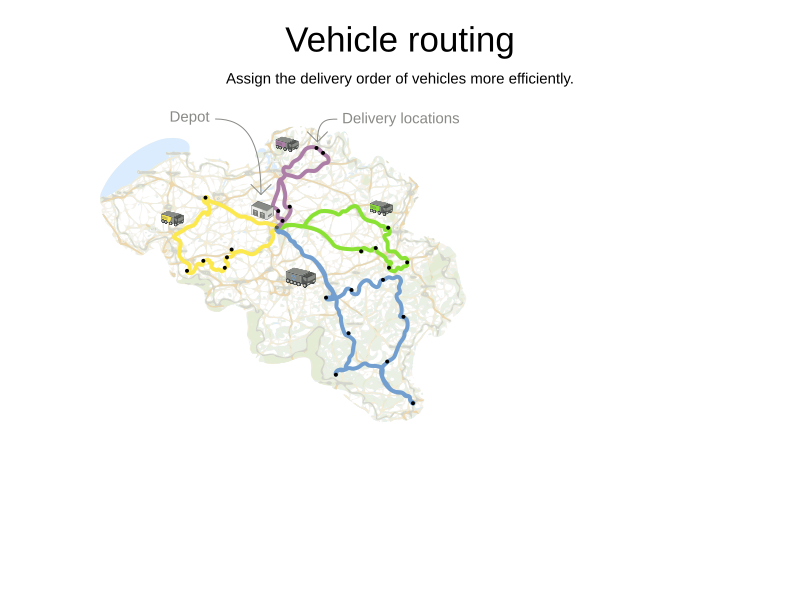
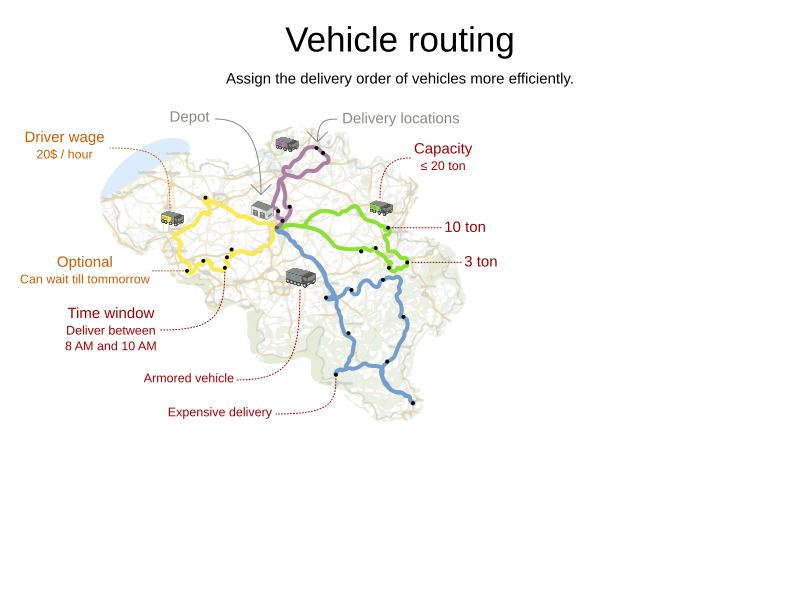

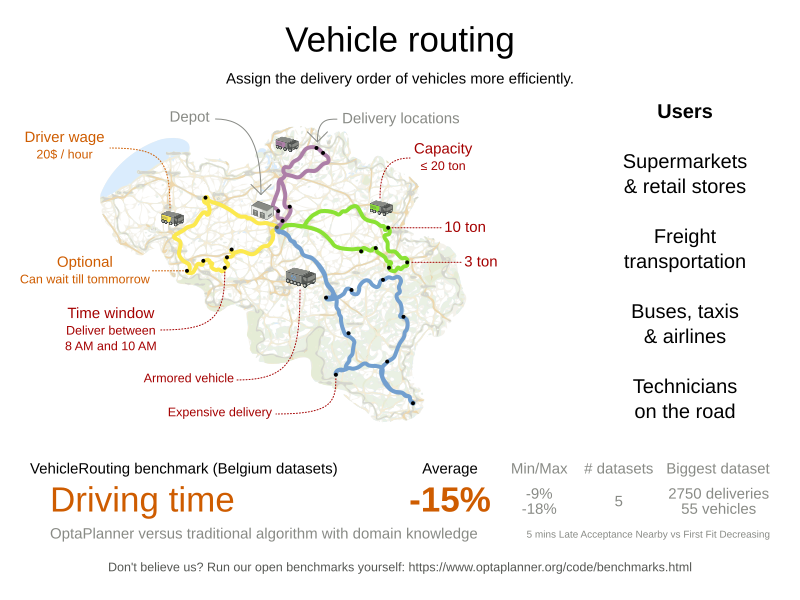
Vehicle Routing Problem (VRP)
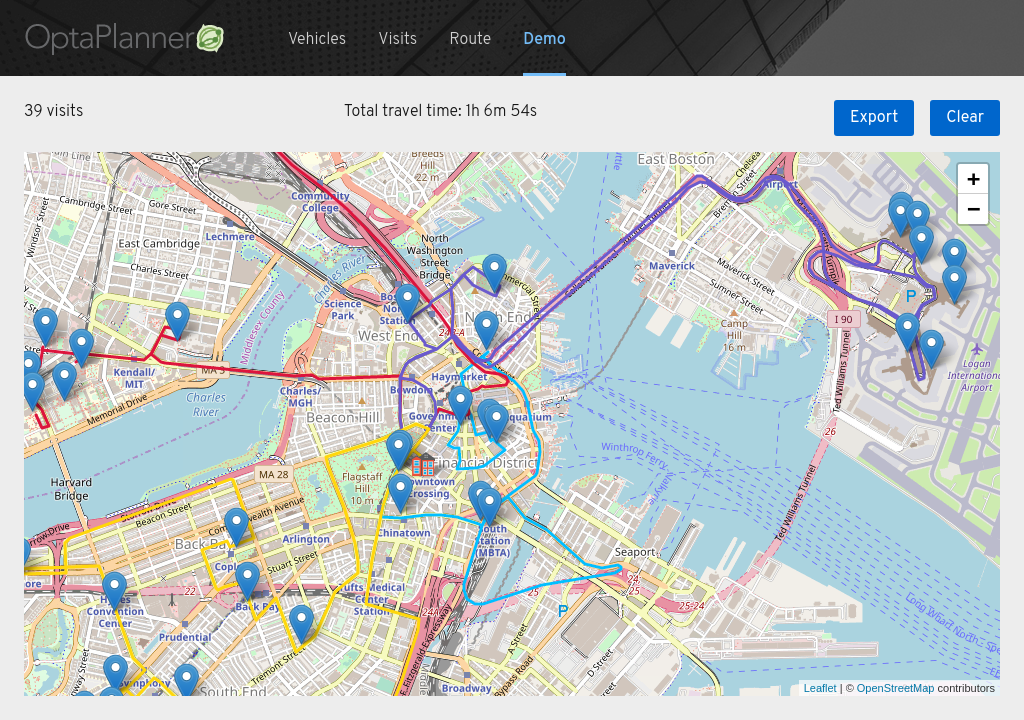
VRP demo
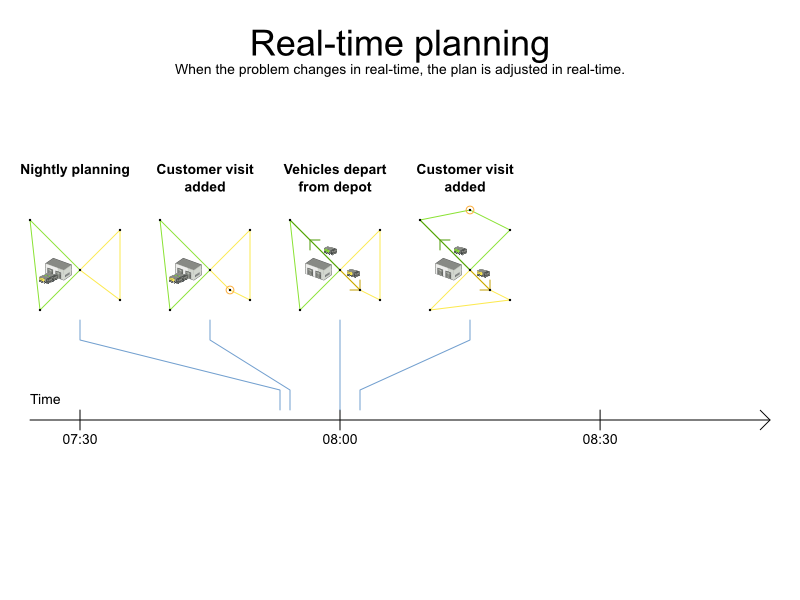
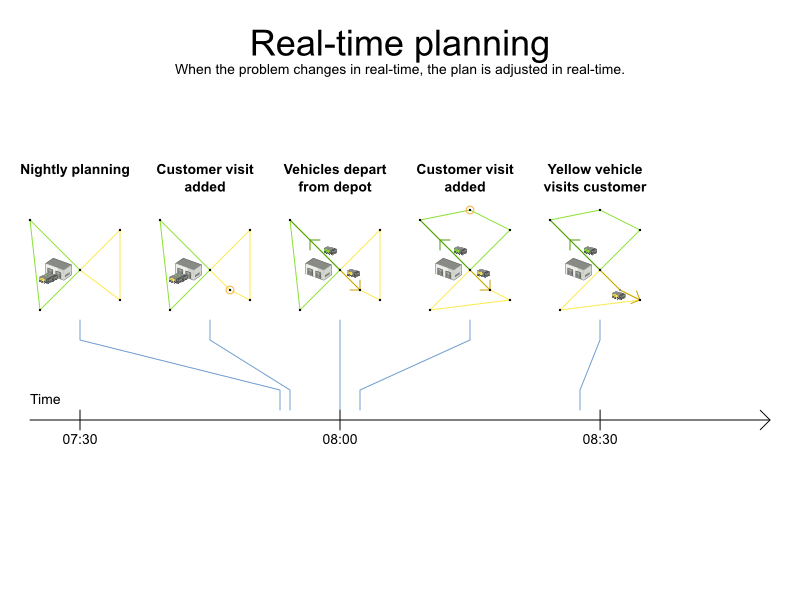
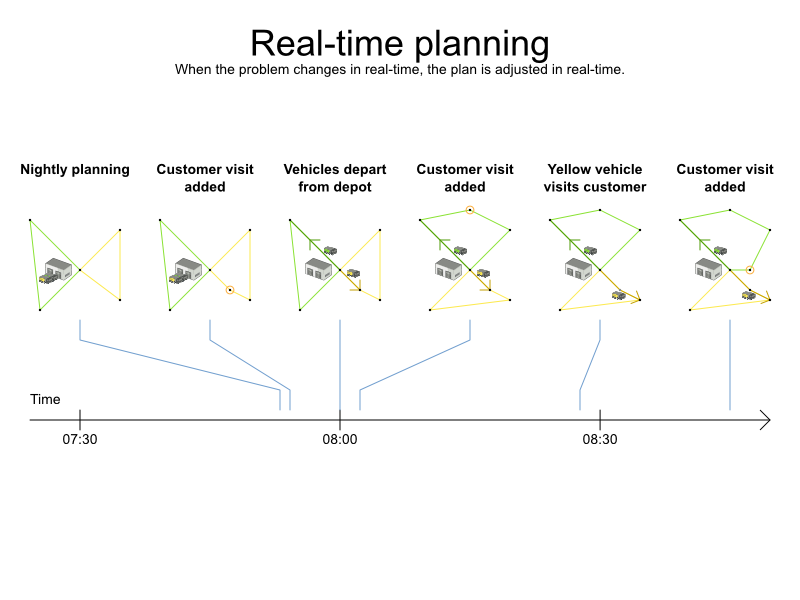
Real-time planning
Warm starts to solve in milliseconds
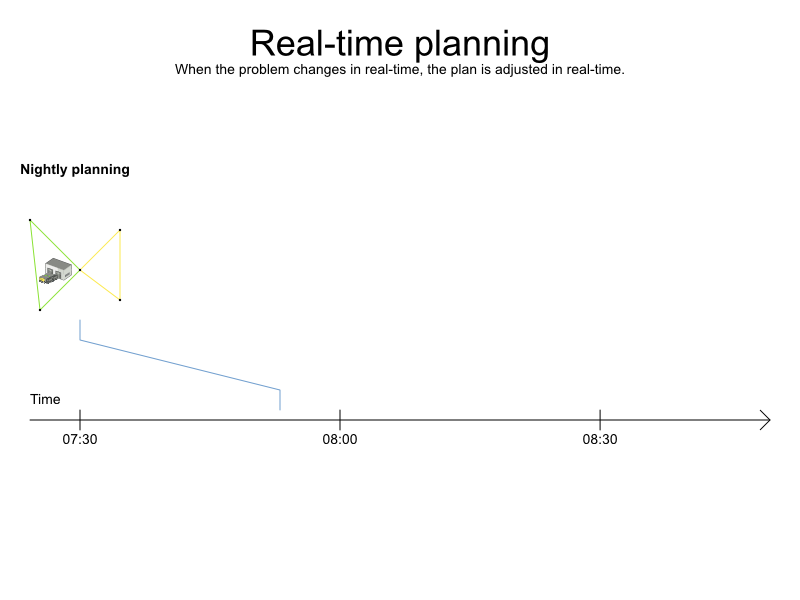
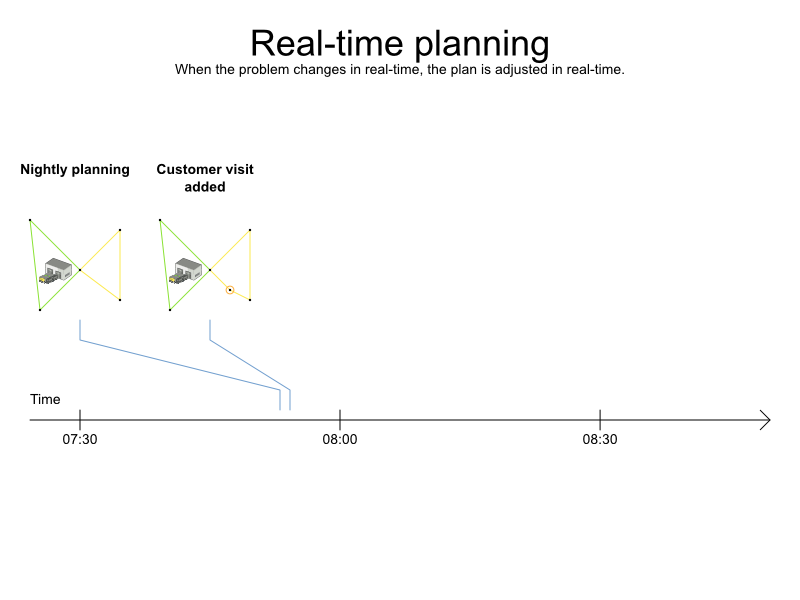
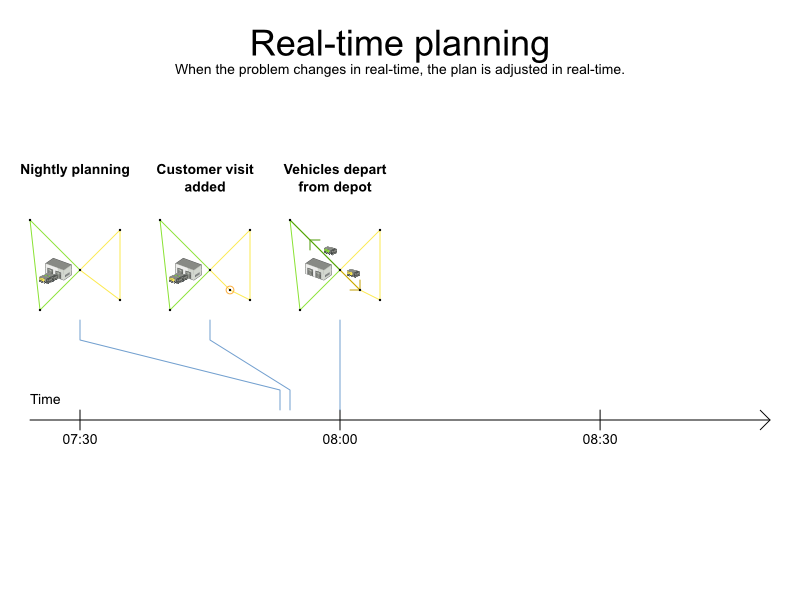
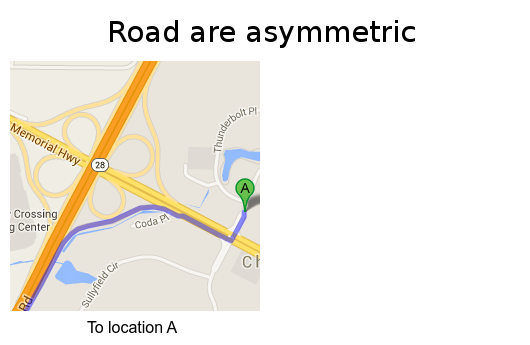
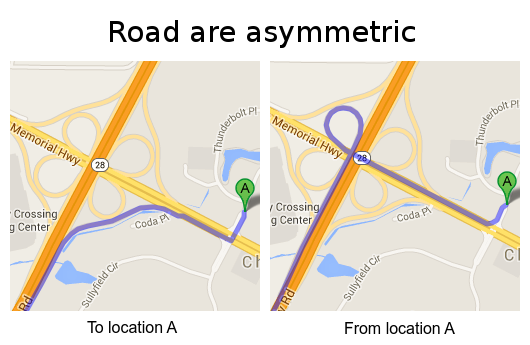
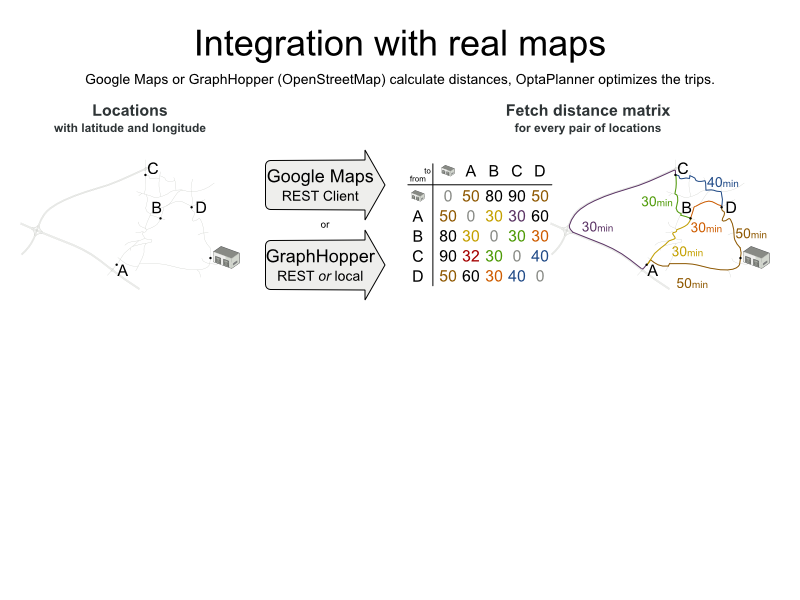
Real roads


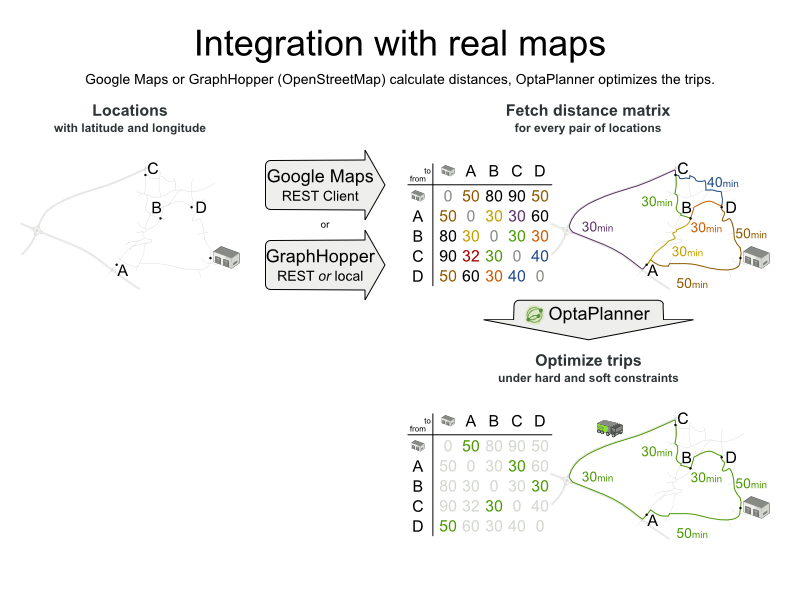
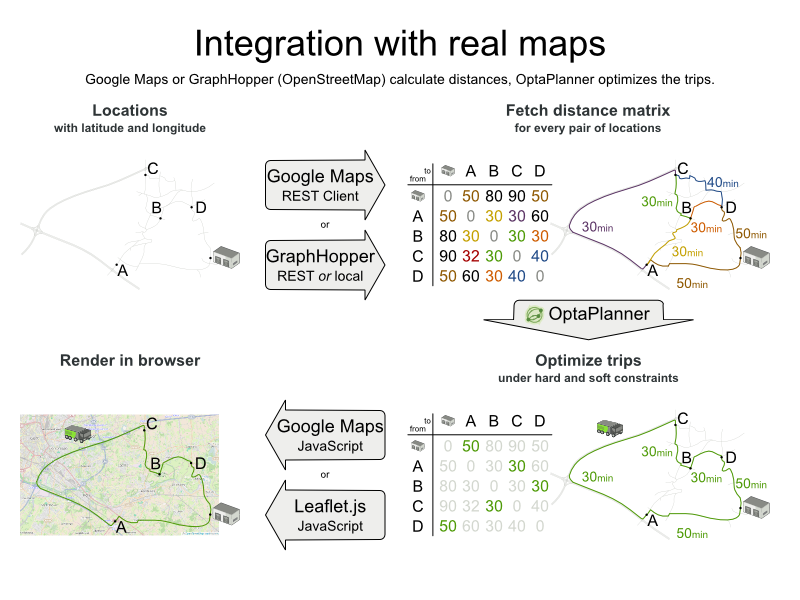
False presumptions VRP
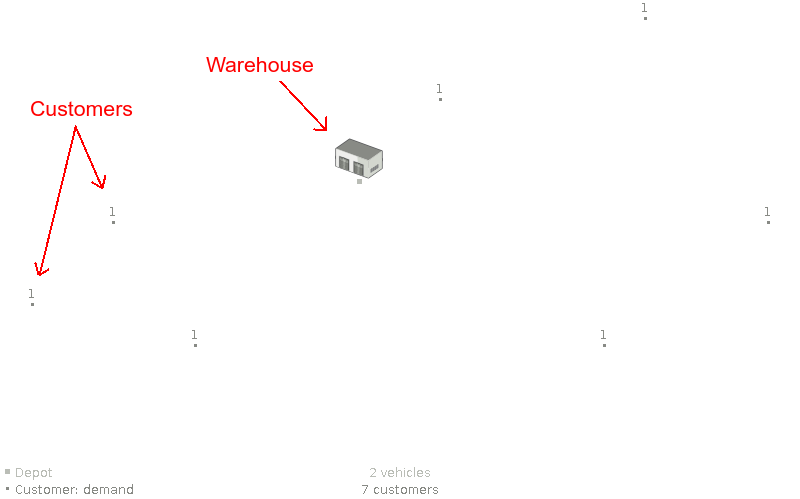
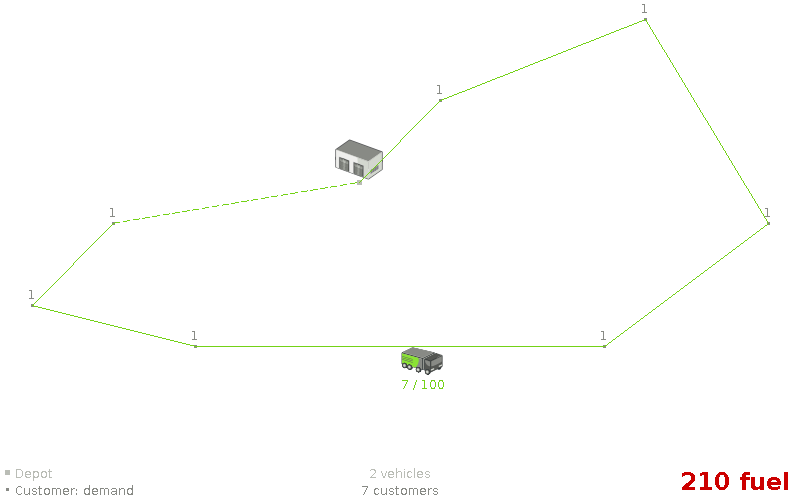
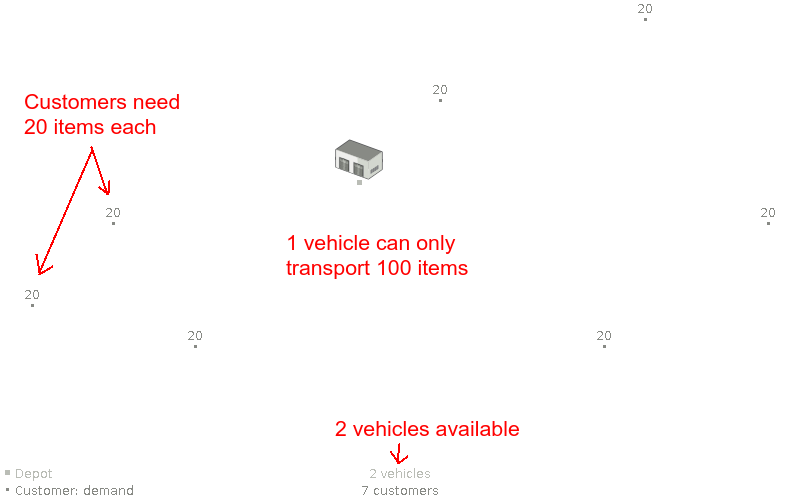
Assumption: An optimal VRP route uses only 1 vehicle.
Assumption: An optimal VRP route uses only 1 vehicle. (false)
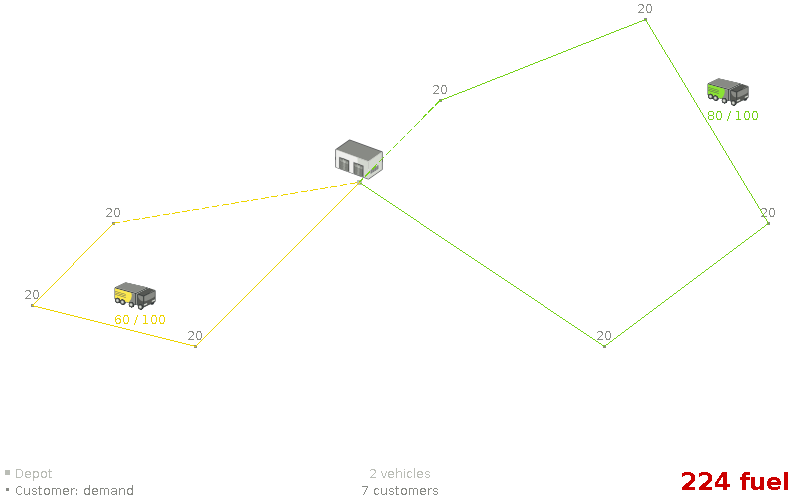
Assumption: An optimal VRP route has no crossing lines.
Assumption: An optimal VRP route has no crossing lines. (false)

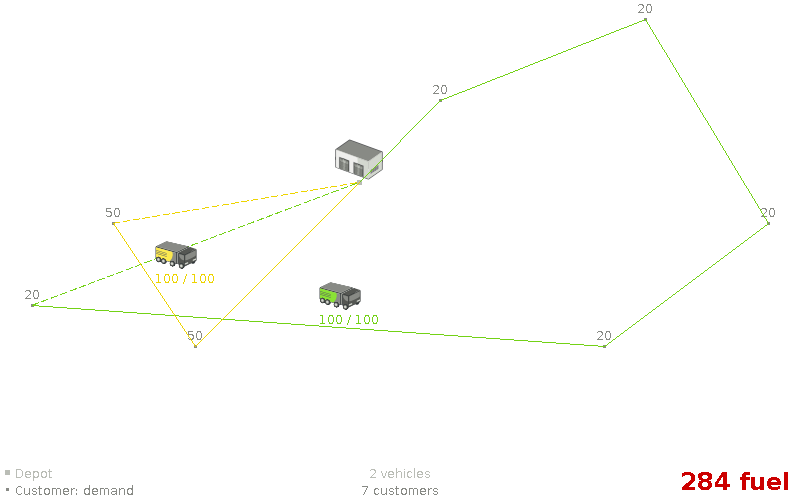
Assumption: An optimal, feasible VRP route with n vehicles is still optimal for n+1 vehicles.
Assumption: An optimal, feasible VRP route with n vehicles is still optimal for n+1 vehicles. (false)
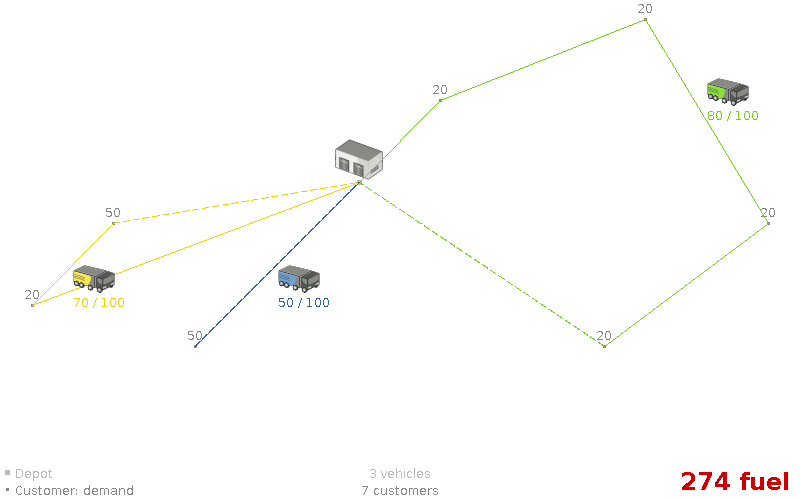
Assumption: An optimal VRP route has no crossing lines of the same color.
Assumption: An optimal VRP route has no crossing lines of the same color. (false)
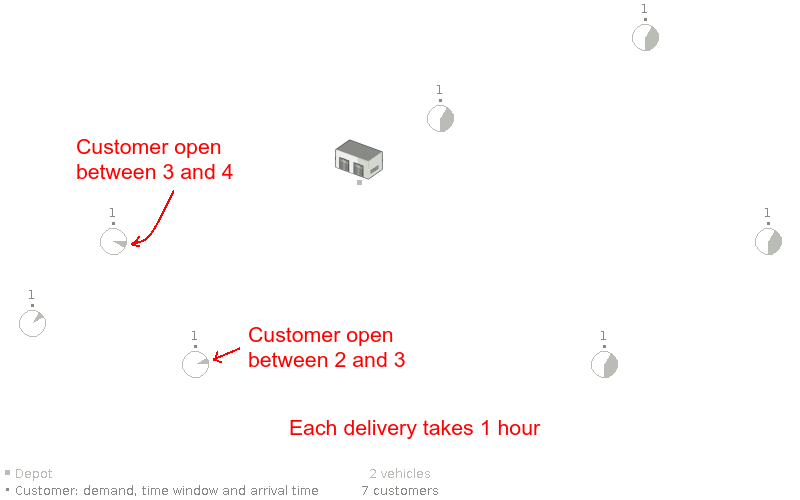
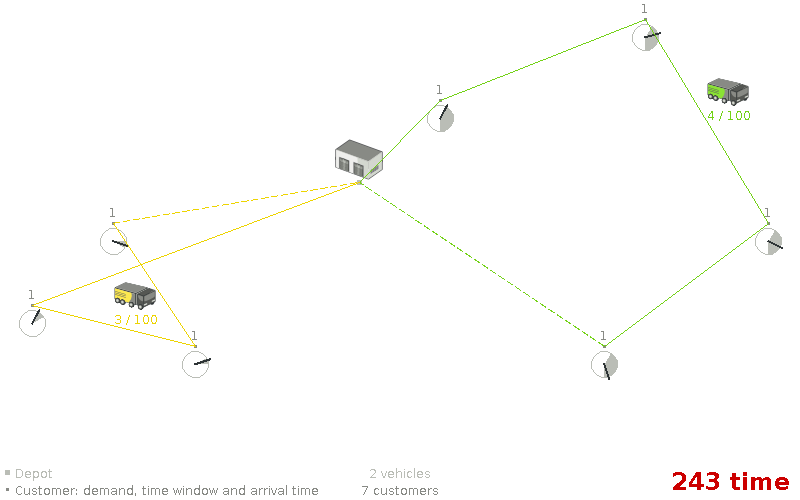
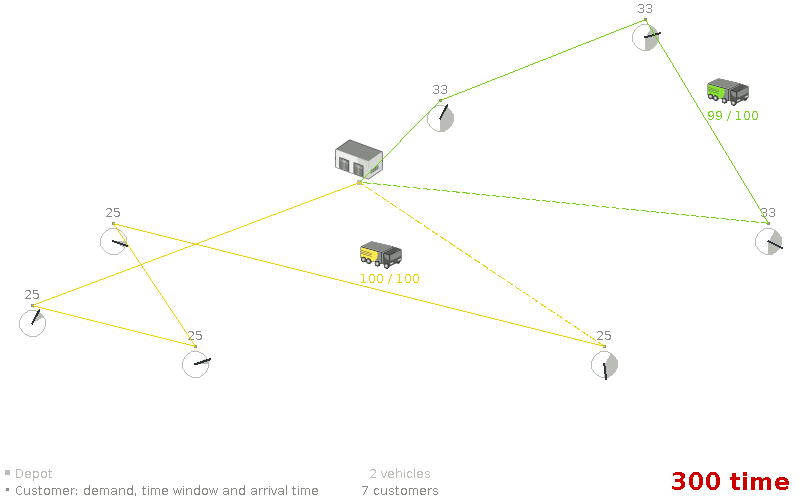
Assumption: We can focus on time windows before focusing on capacity (or vice versa).
Assumption: We can focus on time windows before focusing on capacity (or vice versa). (false)

Assumption: Humans optimize VRP optimally.
Assumption: Humans optimize VRP optimally. (false)
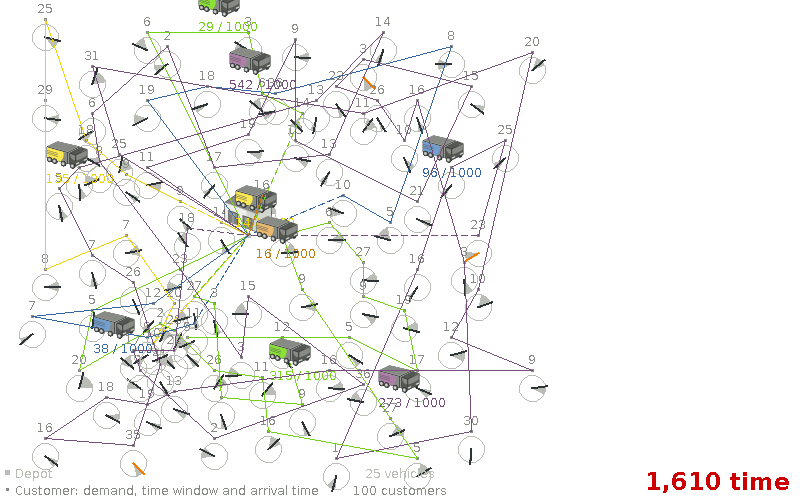
Can a manager reasonable judge if this is optimal?


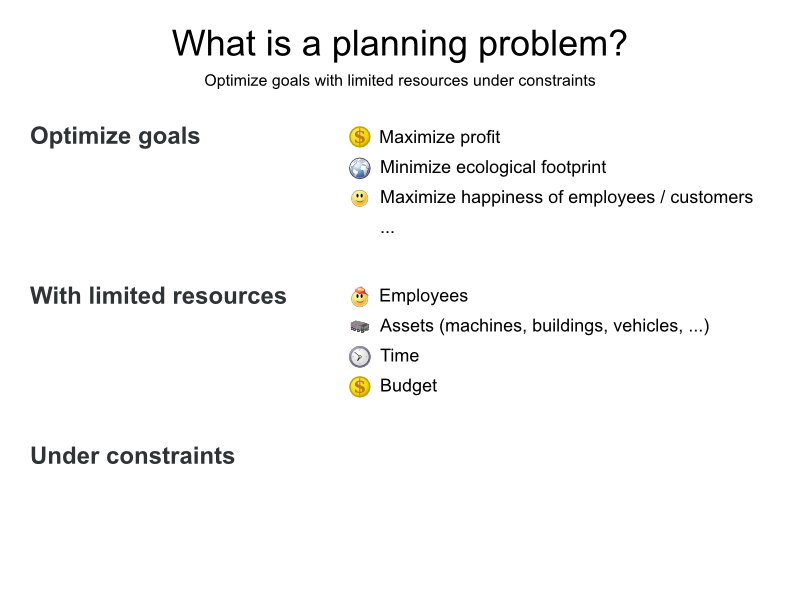


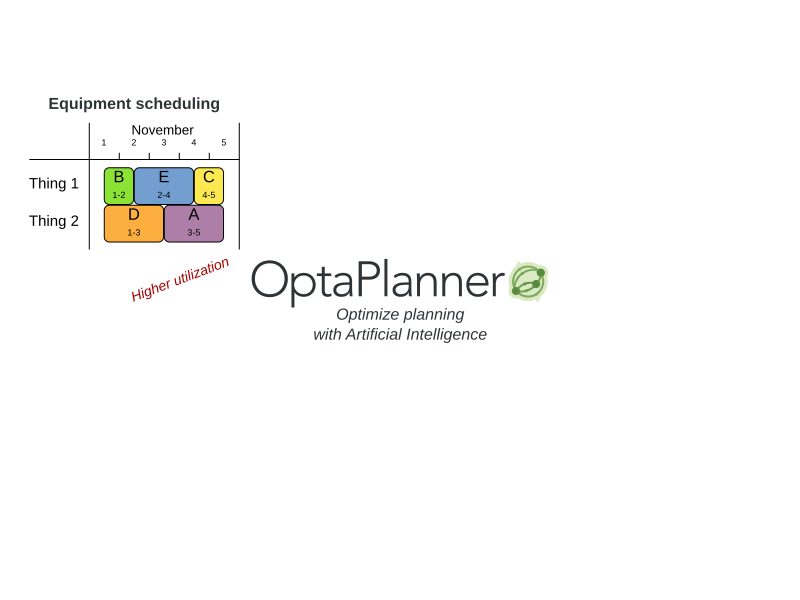
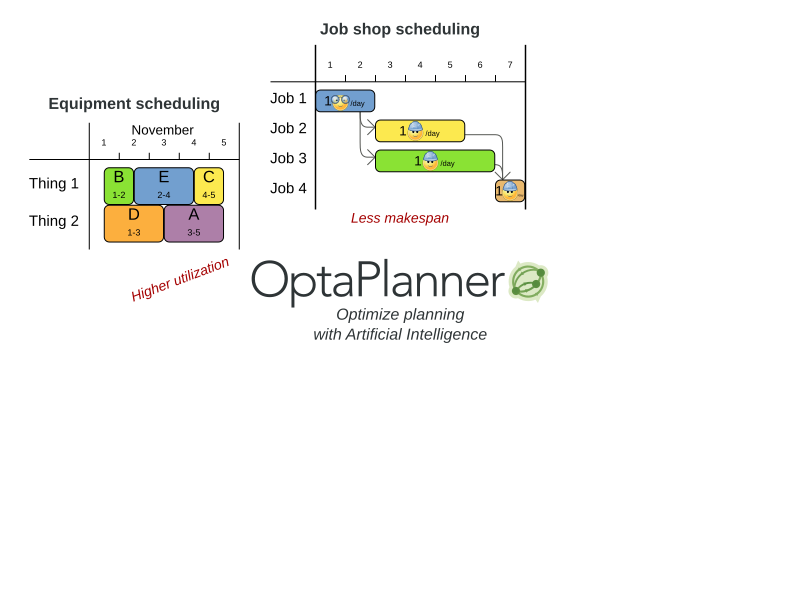
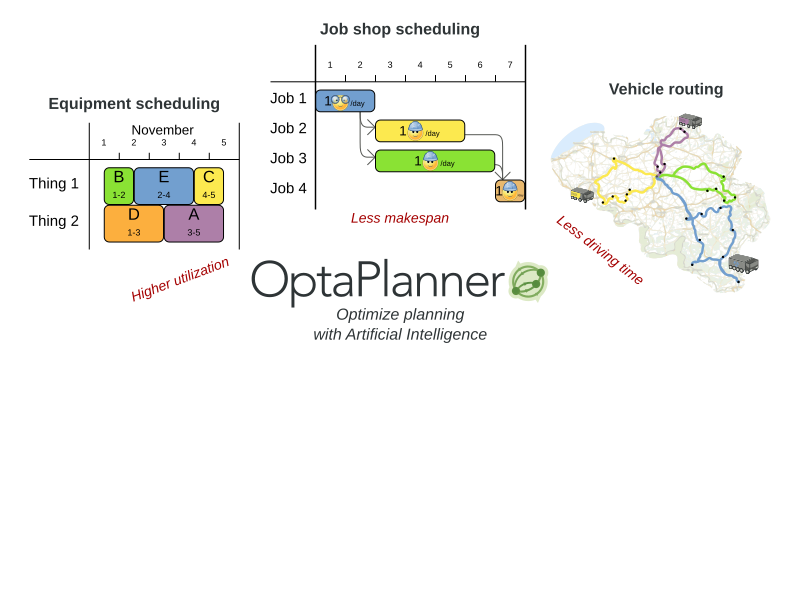
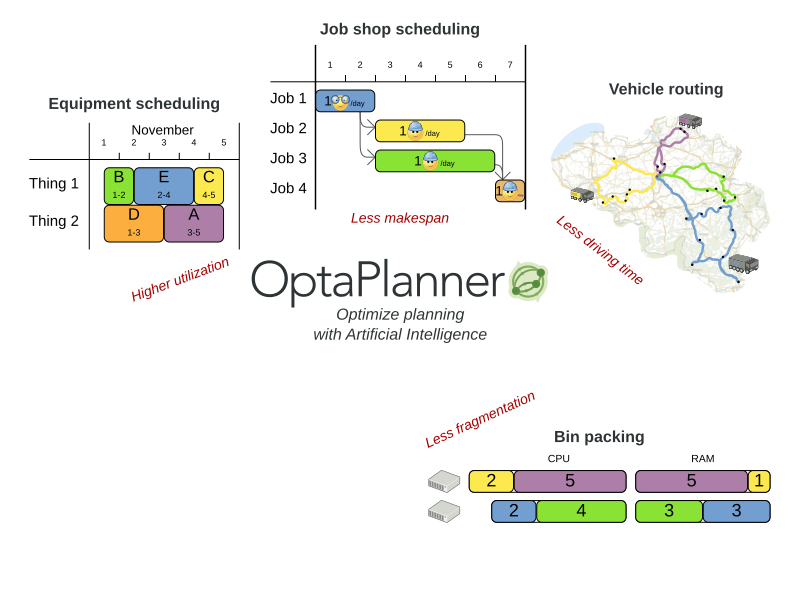
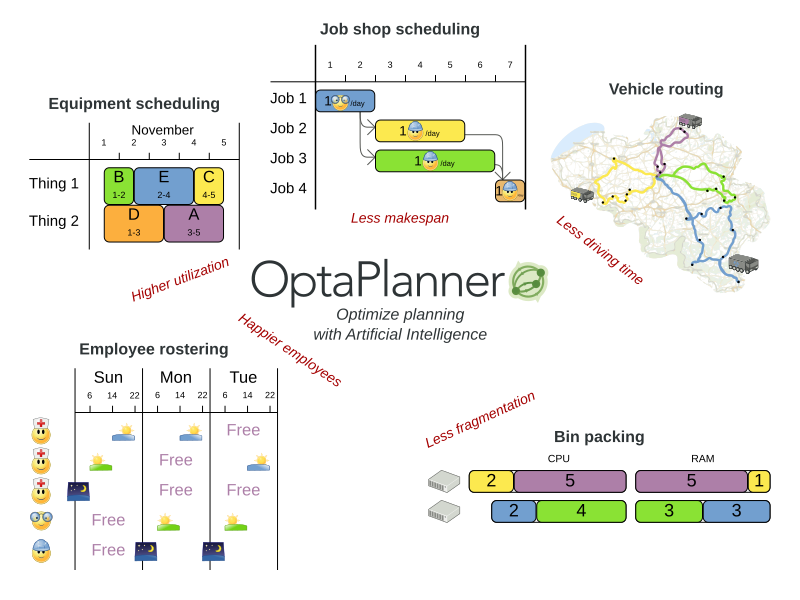
Planning problem use cases
- Agenda scheduling: doctor appointments, court hearings,
maintenance jobs, TV advertisements, ... - Educational timetabling: lectures, exams, conference talks, ...
- Task assignment: affinity/skill matchmaking for audits, ...
- Employee shift rostering: nurses, help desk, guards, firemen, ...
- Vehicle routing: route trucks, buses, trains, boats, airplanes, ...
- Bin packing: fill containers, trucks, ships, storage warehouses,
cloud computers nodes, prisons, hospitals, ... - Job shop scheduling: assembly lines for cars, furniture, books, ...
- Cutting stock: minimize waste while cutting paper, steel, carpet, ...
- Sport scheduling: football/baseball league, tennis courts, ...
- Financial optimization: investment portfolio risk balance, ...
Reuse optimization algorithms

Find better solutions in time and scale out
- Open source - Apache License
- Regular releases - available on Maven Central
- Documented - reference manual and examples
- Quality coverage - unit, integration and stress tests



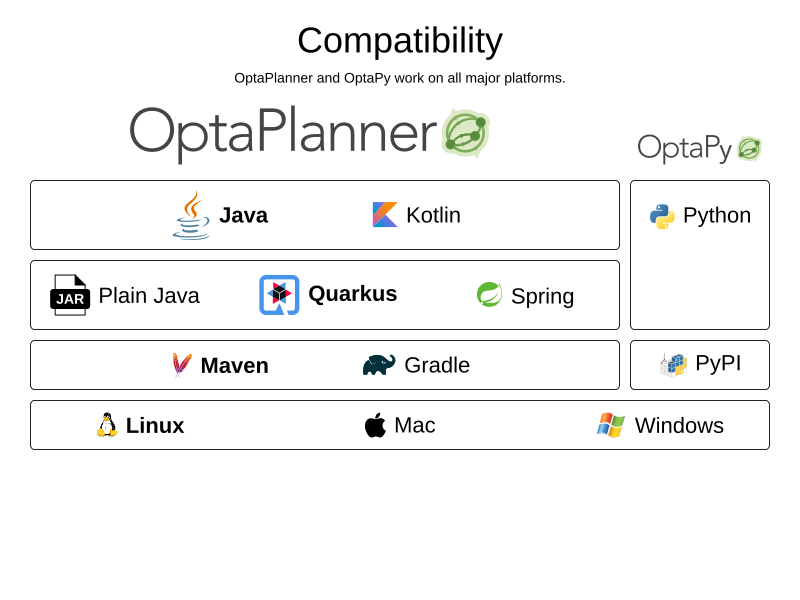
Is this A.I.?





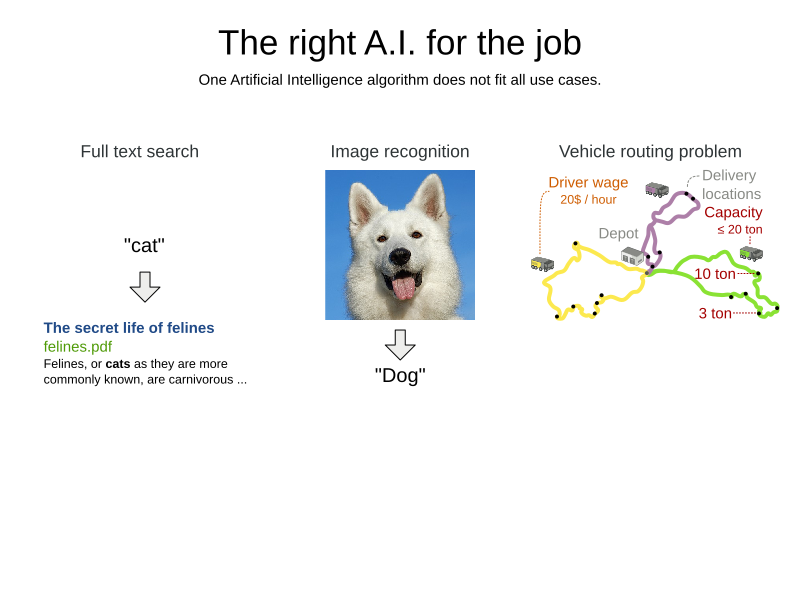
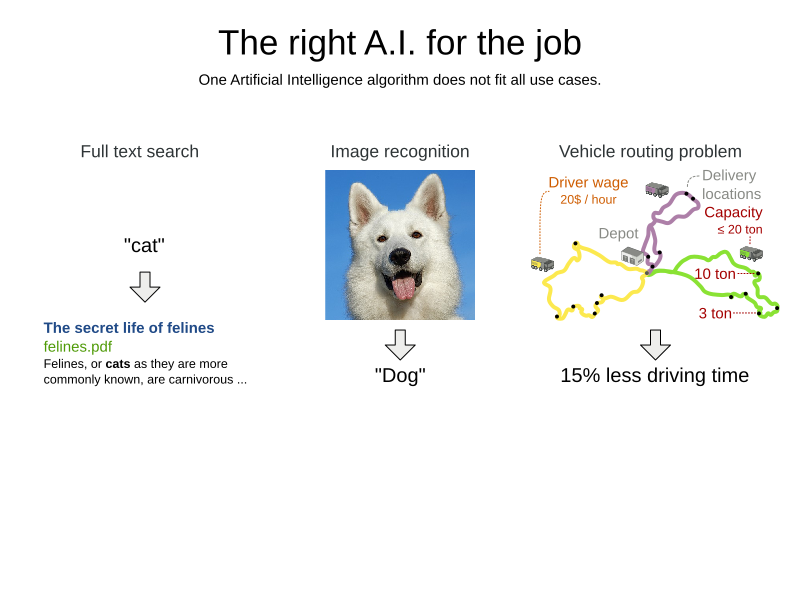
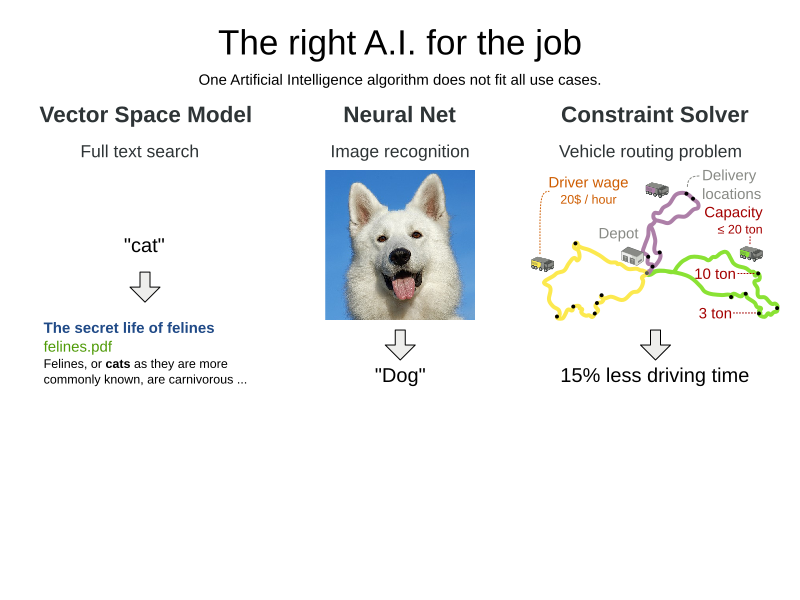
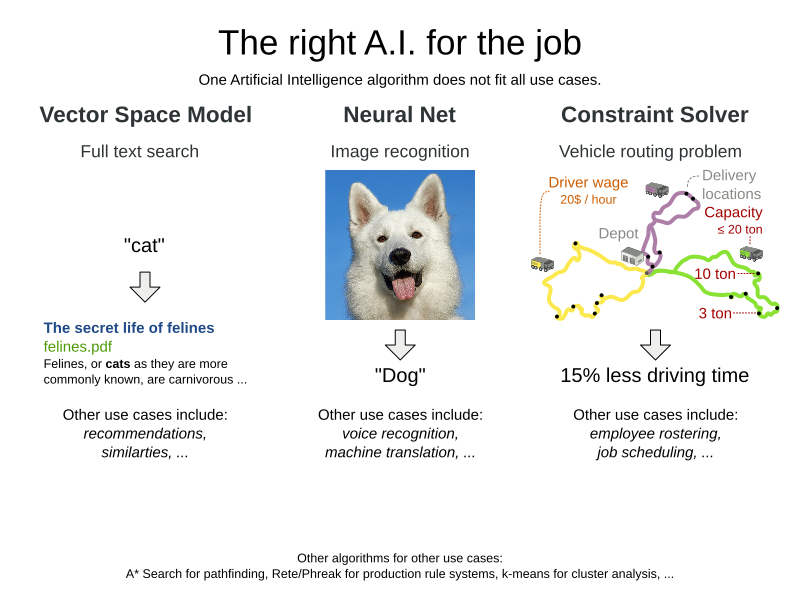
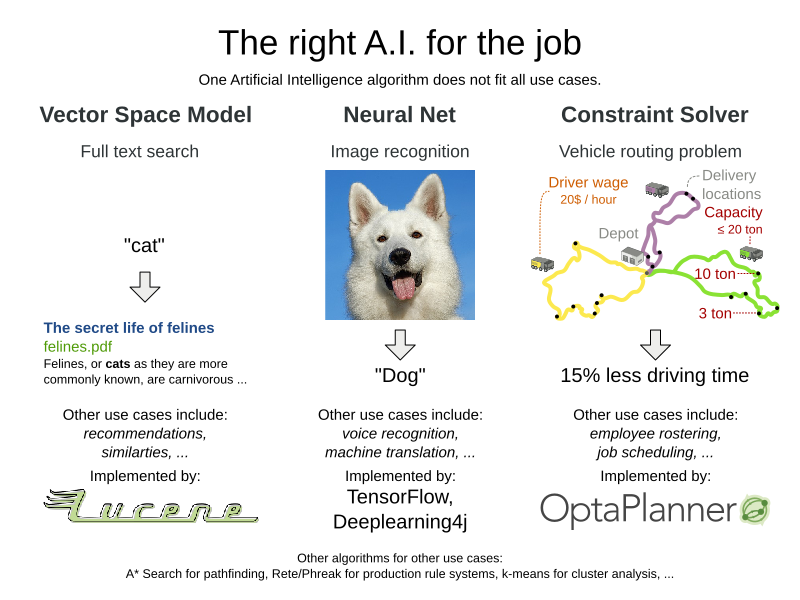
Employee Rostering (technical)
Press down to show
Press right to skip
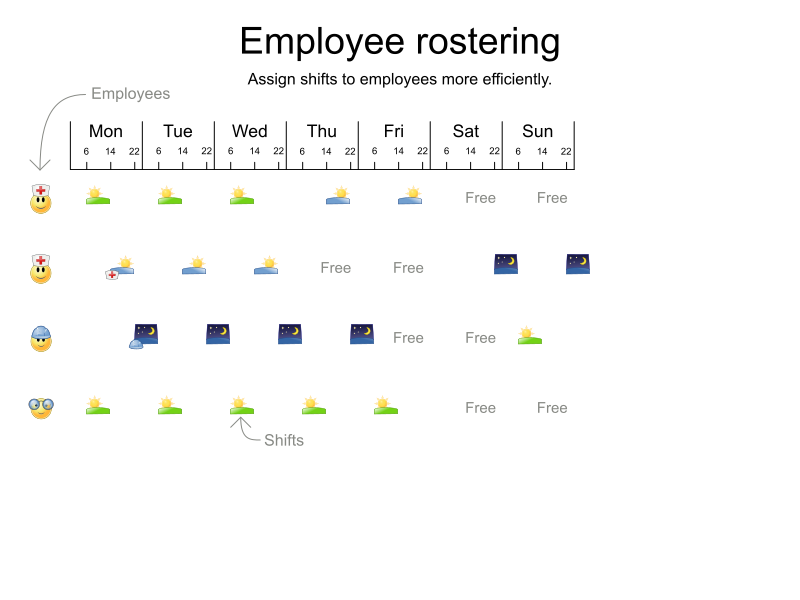
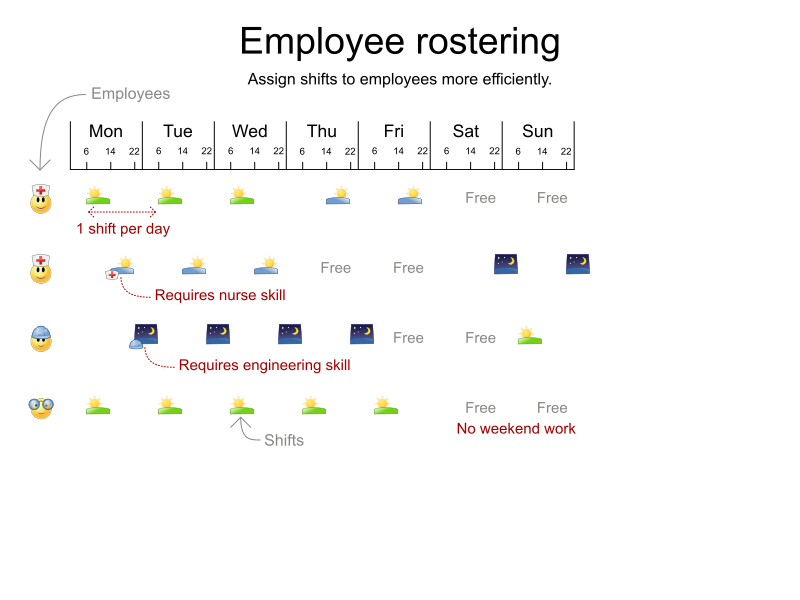
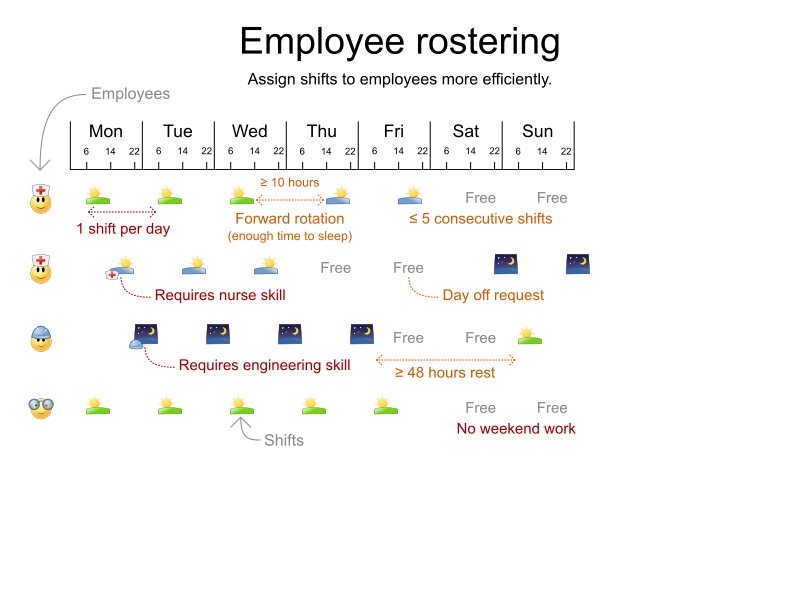
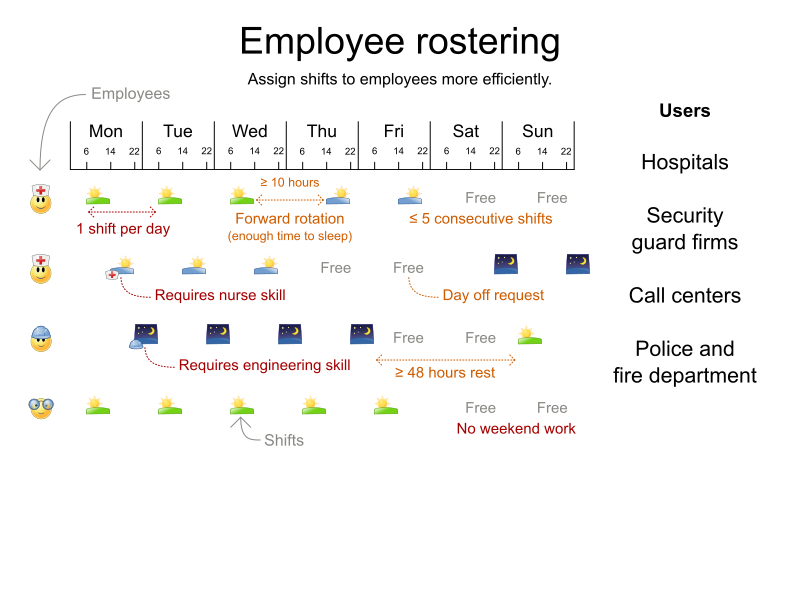
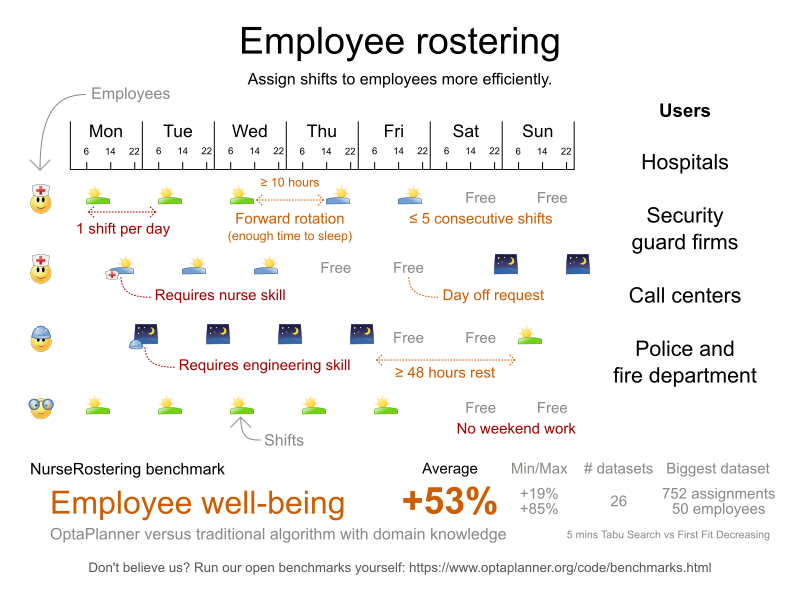
What is constraint solving?

OptaWeb Employee Rostering demo
Implementation
- Define domain
- Define constraints
- Solve
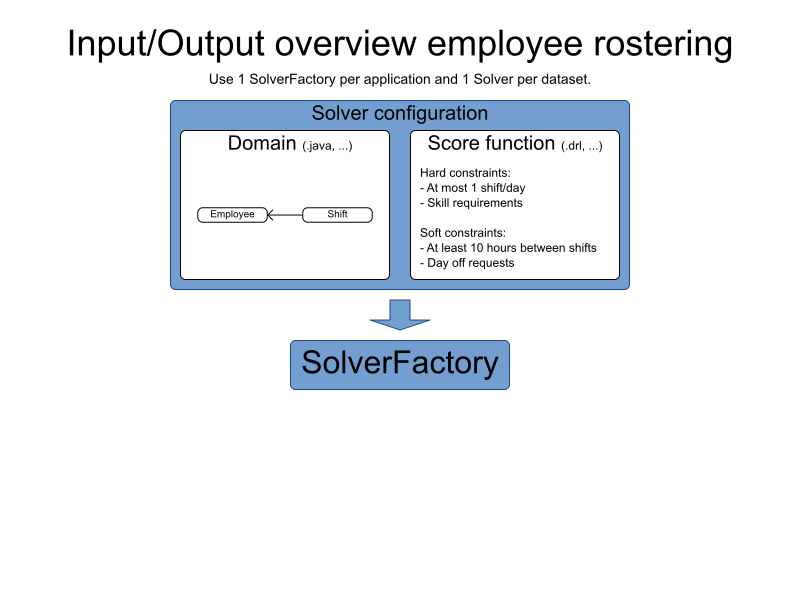
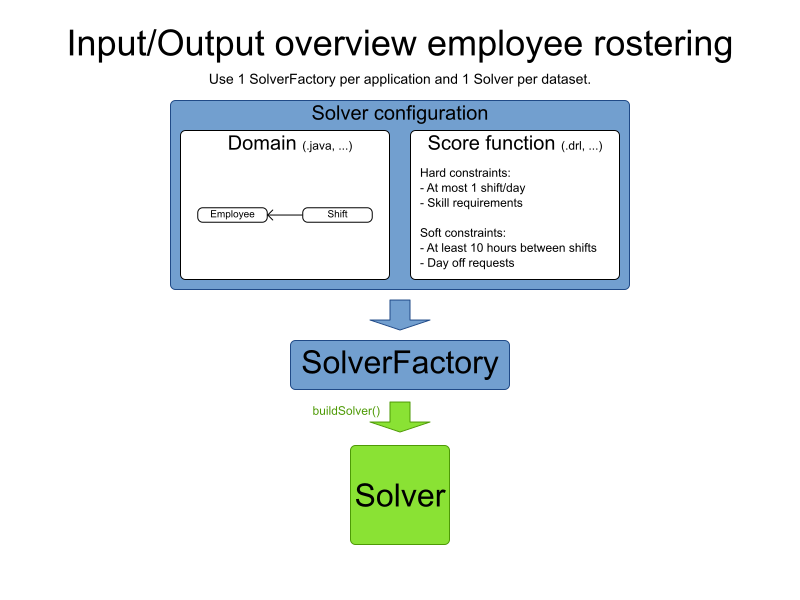
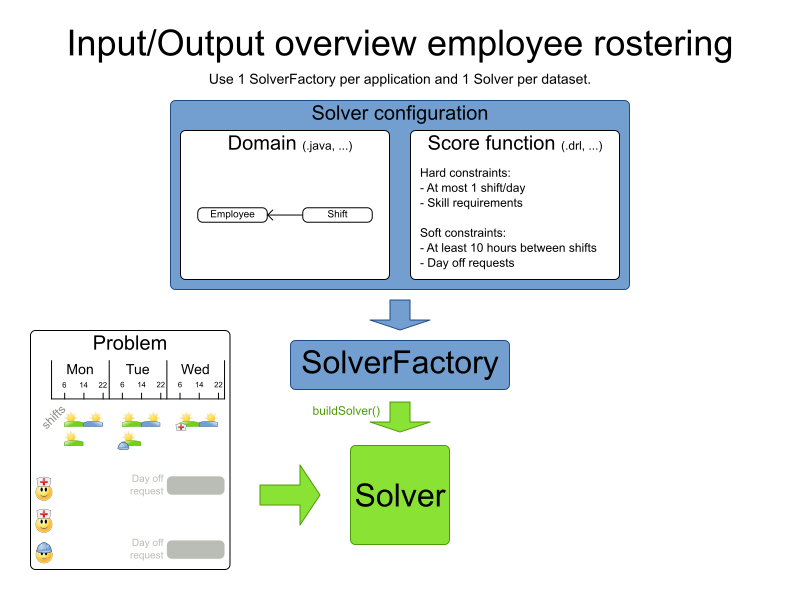
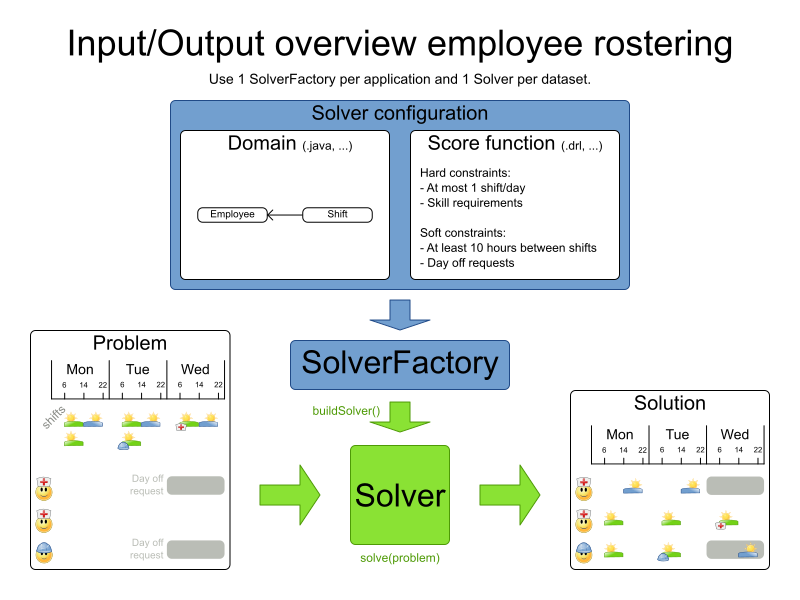
Calling the solve method
// My domain specific class as input
Roster problem = ...;
SolverFactory<Roster> factory = SolverFactory
.createFromXmlResource(".../mySolverConfig.xml");
Solver<Roster> solver = factory.buildSolver();
// My domain specific class as output
Roster solution = solver.solve(problem);
for (Shift shift : solution.getShiftList()) {
// Each shift is now assigned to an employee
System.out.println(shift + ": " + shift.getEmployee());
}Define domain
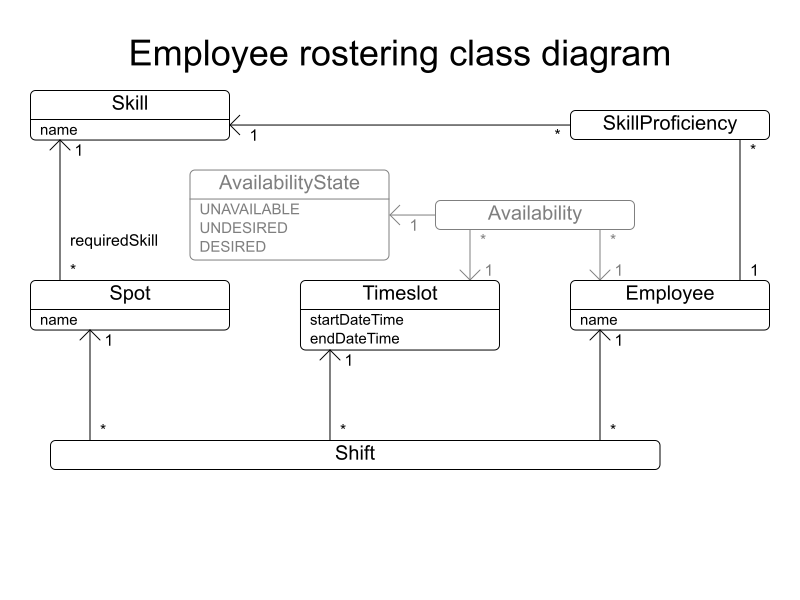
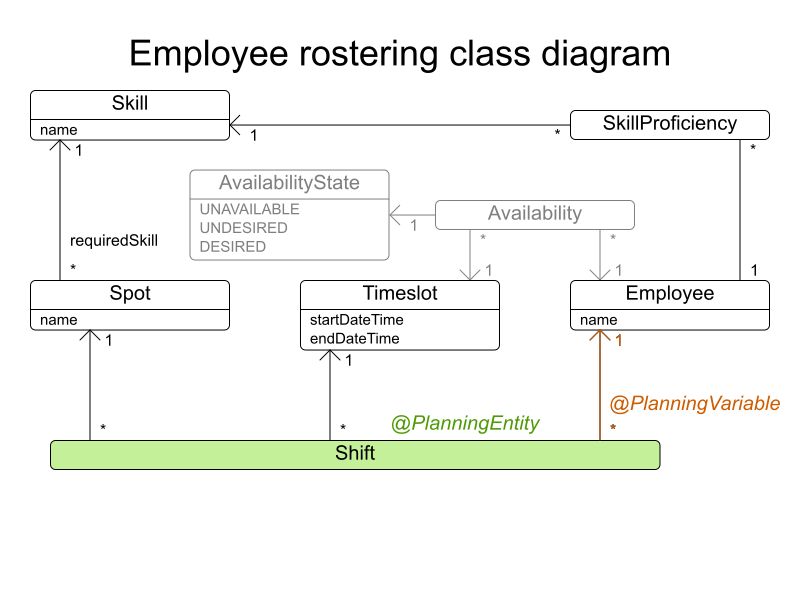
Spot.java
public class Spot {
private String name;
private Skill requiredSkill;
...
}Plain old java class
Employee.java
public class Employee {
private String name;
private List<Skill> skillList;
...
public boolean hasSkill(Skill skill) {
return skillList.contains(skill);
}
}Plain old java class
Shift.java
@PlanningEntity
public class Shift {
private Spot spot;
private TimeSlot timeSlot;
@PlanningVariable(...)
private Employee employee; // Changes during solve()
...
}Plain old java class with OptaPlanner annotations
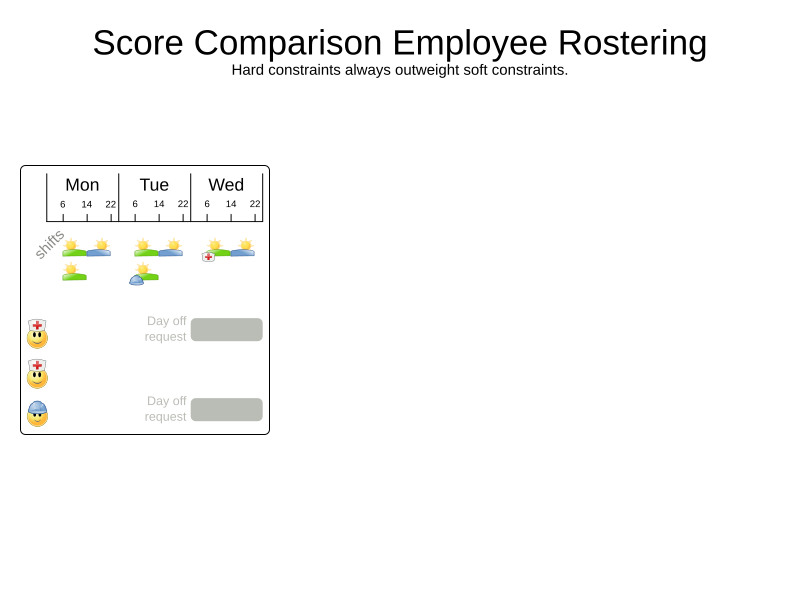
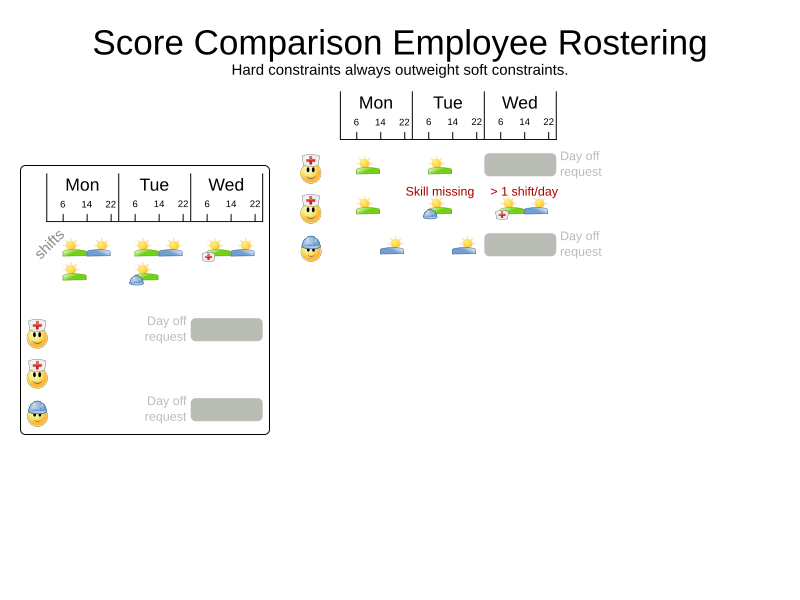
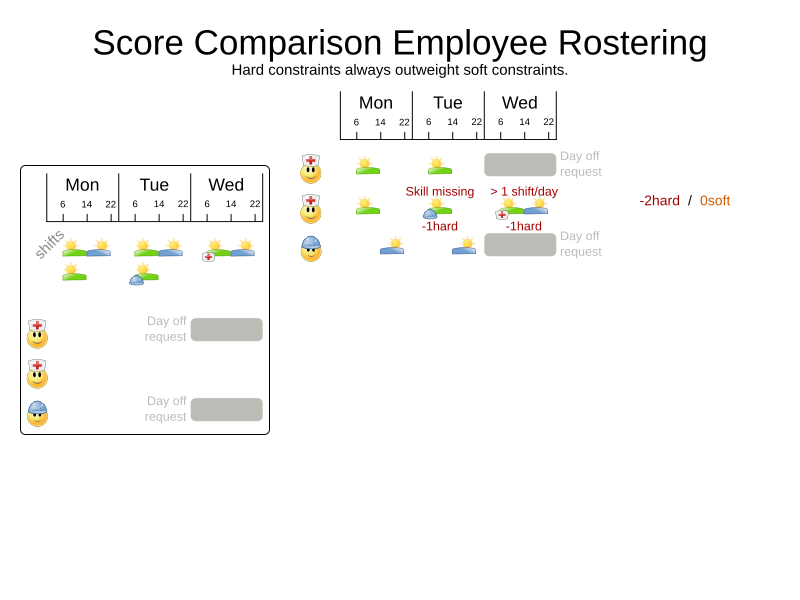
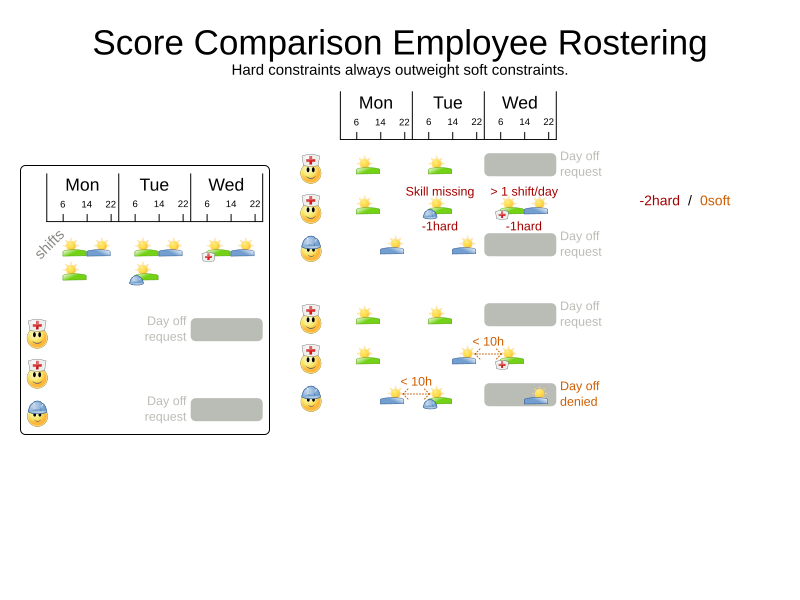
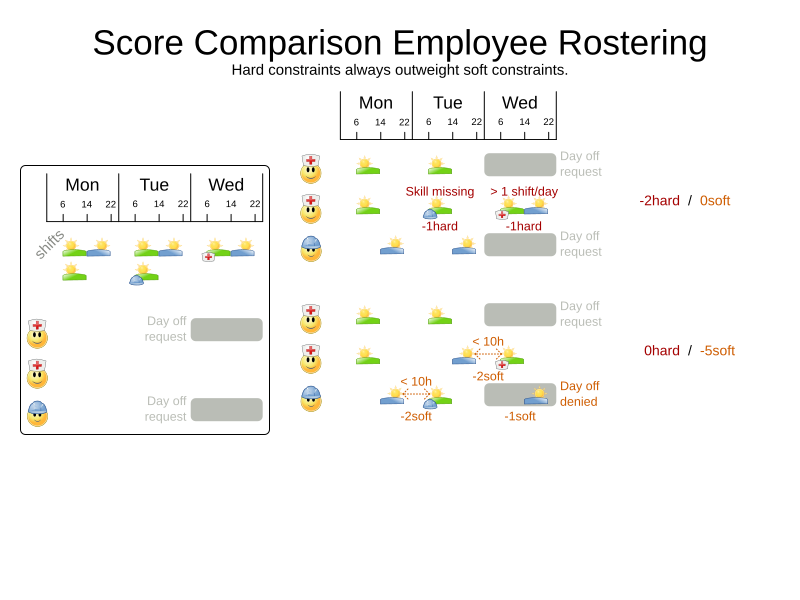
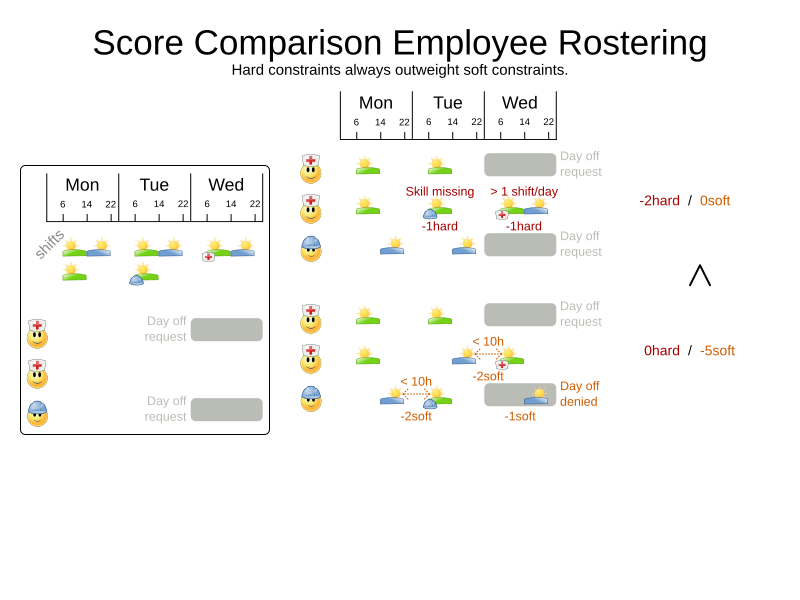
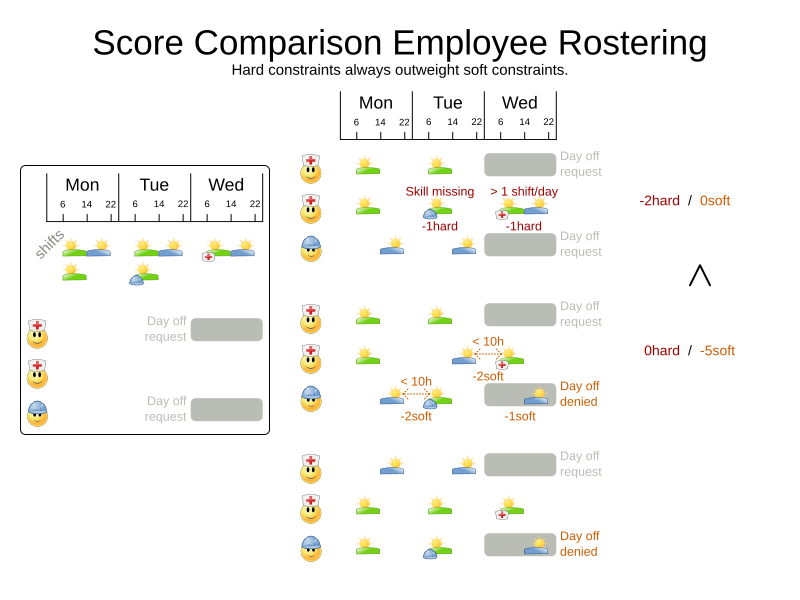
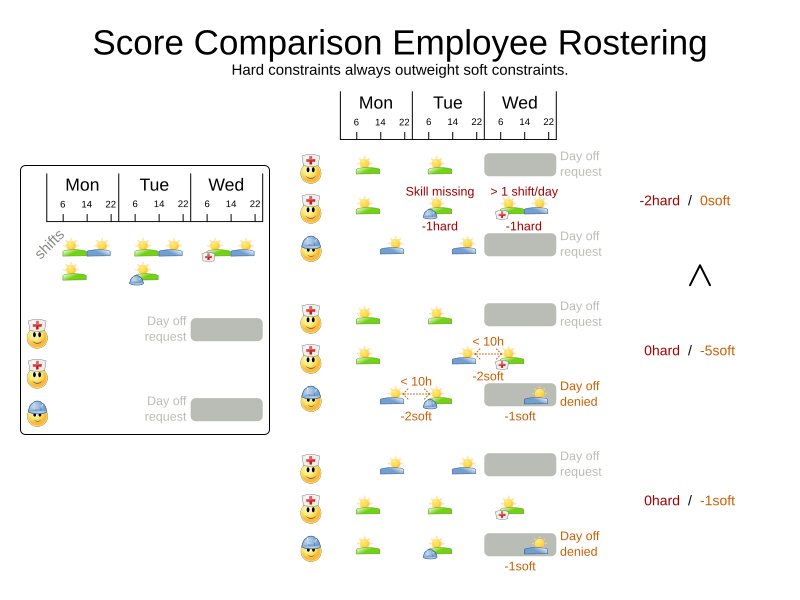
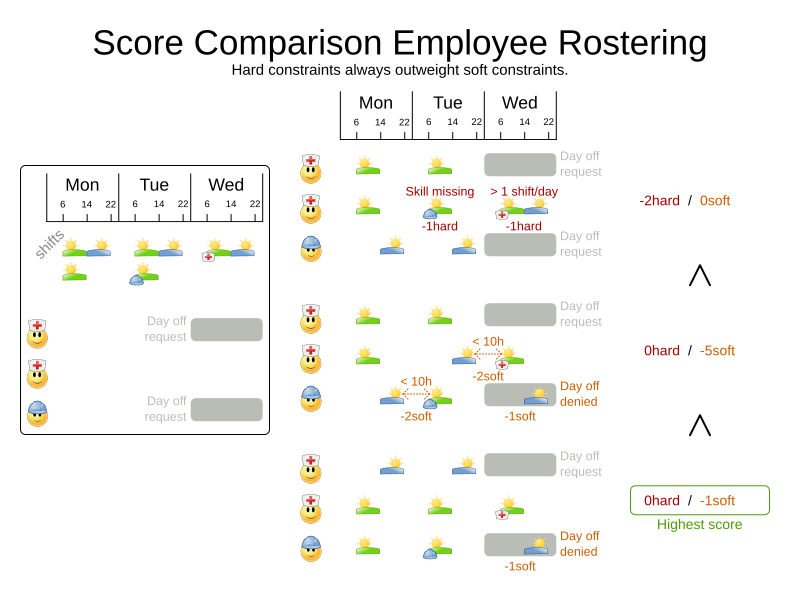
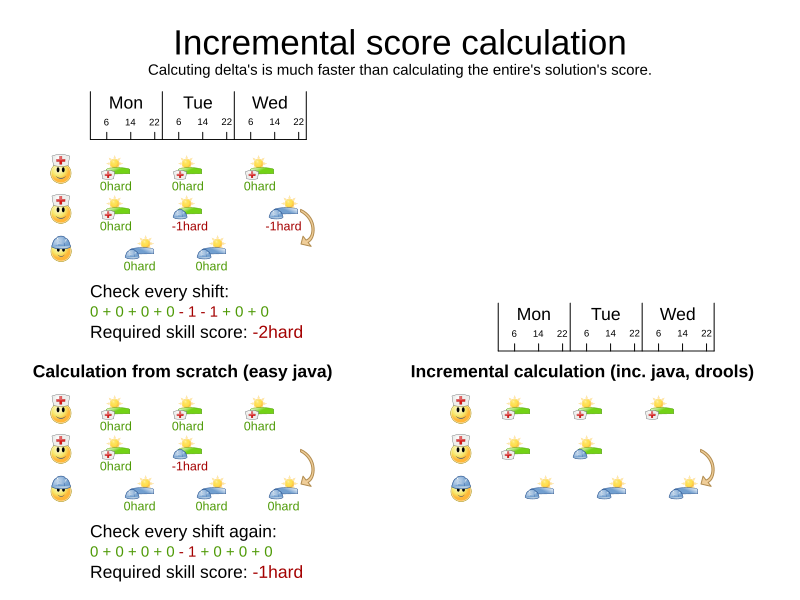
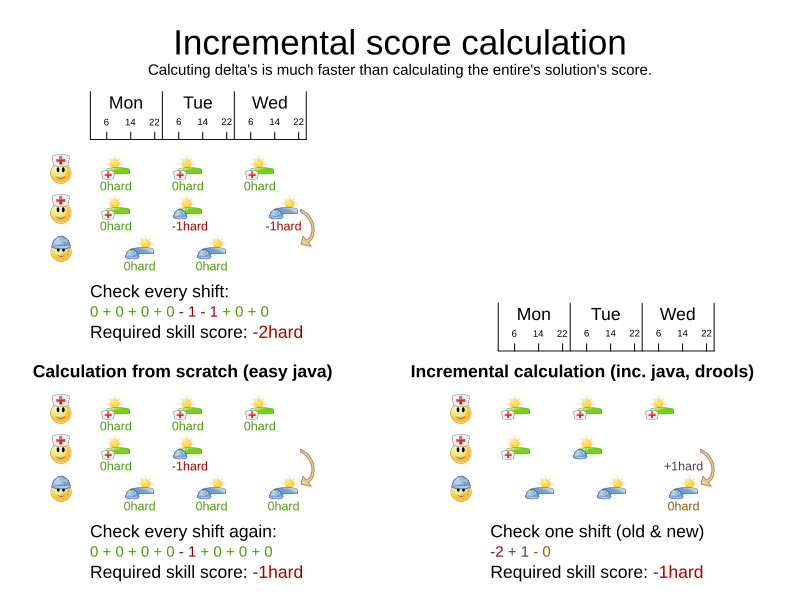
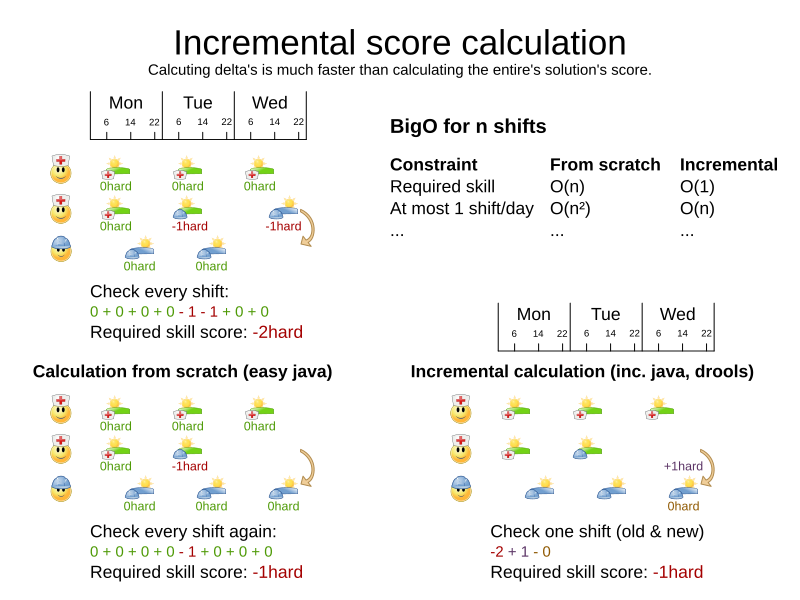
Score calculation
- Easy Java
- Incremental Java
- Drools DRL (also incremental)
Required skill constraint (Java)
public class MyScoreCalculator
implements EasyScoreCalculator<Roster> {
public Score calculateScore(Roster roster) {
int hardScore = 0;
for (Shift shift : roster.getShiftList()) {
Skill requiredSkill = shift.getSpot().getRequiredSkill();
if (shift.getEmployee() != null
// Employee lacks required skill
&& !shift.getEmployee().hasSkill(requiredSkill)) {
// Lower hard score
hardScore--;
}
}
...
return HardSoftScore.valueOf(hardScore, softScore);
}
}

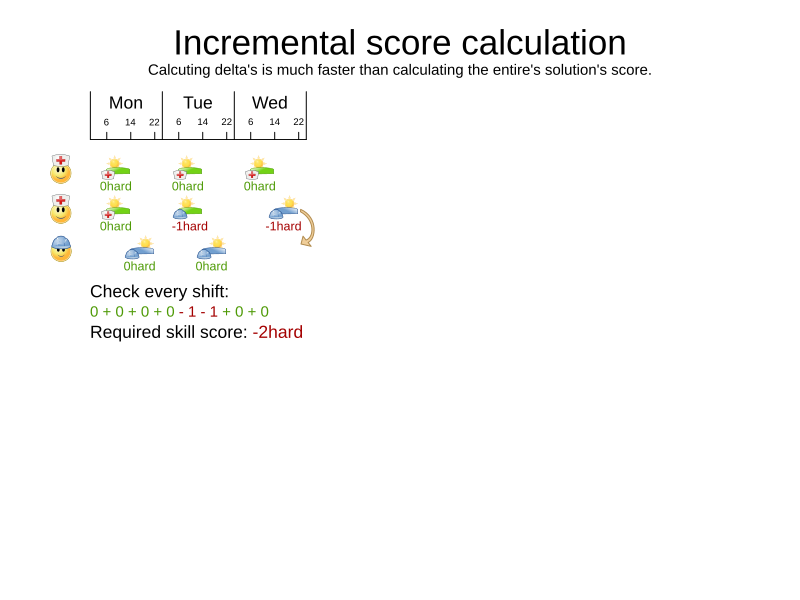

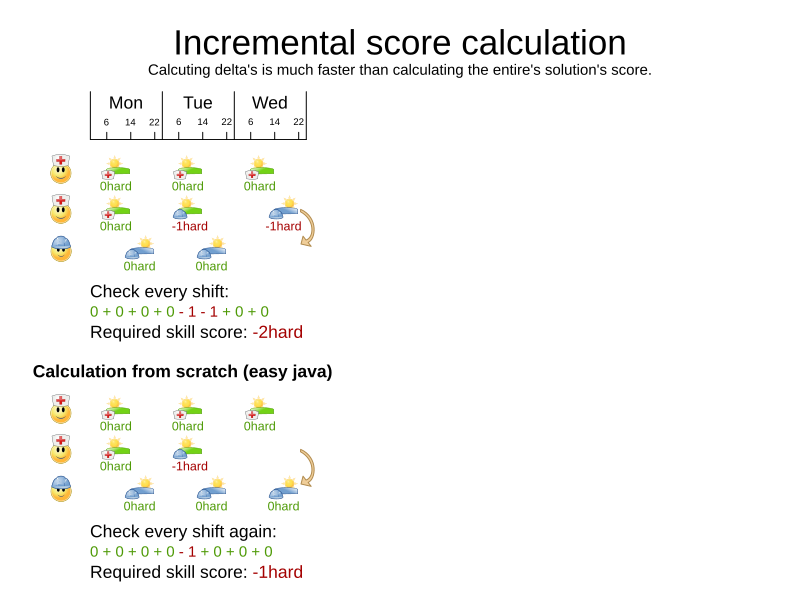
Required skill constraint (DRL)
rule "Required skill"
when
Shift(
getEmployee() != null,
// Employee lacks required skill
!getEmployee().hasSkill(getSpot().getRequiredSkill()))
then
// Lower hard score
scoreHolder.addHardConstraintMatch(kcontext, -1);
endAvailability.java
public class Availability {
private Employee employee;
private TimeSlot timeSlot;
// UNAVAILABLE, UNDESIRED or DESIRED
private AvailabilityState state;
...
}
Plain old java class
All instances handled by only one constraint
Time off request constraint (Java)
public Score calculateScore(Roster roster) {
...
int softScore = 0;
for (Availability av : roster.getAvailabilityList()) {
for (Shift shift : roster.getShiftList()) {
if (shift.getEmployee() == av.getEmployee()
&& shift.getTimeSlot() == av.getTimeSlot()) {
if (av.getState() == AvailabilityState.UNDESIRED {
// Lower soft score
softScore--;
} else {
...
}
}
}
}
return HardSoftScore.valueOf(hardScore, softScore);
}Time off request constraint (DRL)
rule "Time off request"
when
Availability(
state == AvailabilityState.UNDESIRED,
$e : employee,
$t : timeSlot)
Shift(
employee == $e,
timeSlot == $t)
then
// Lower soft score
scoreHolder.addSoftConstraintMatch(kcontext, -1);
end
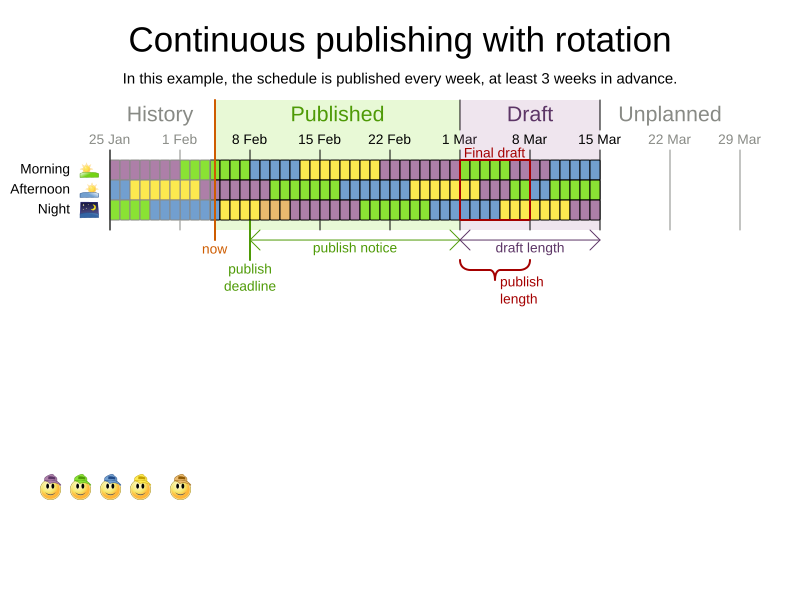
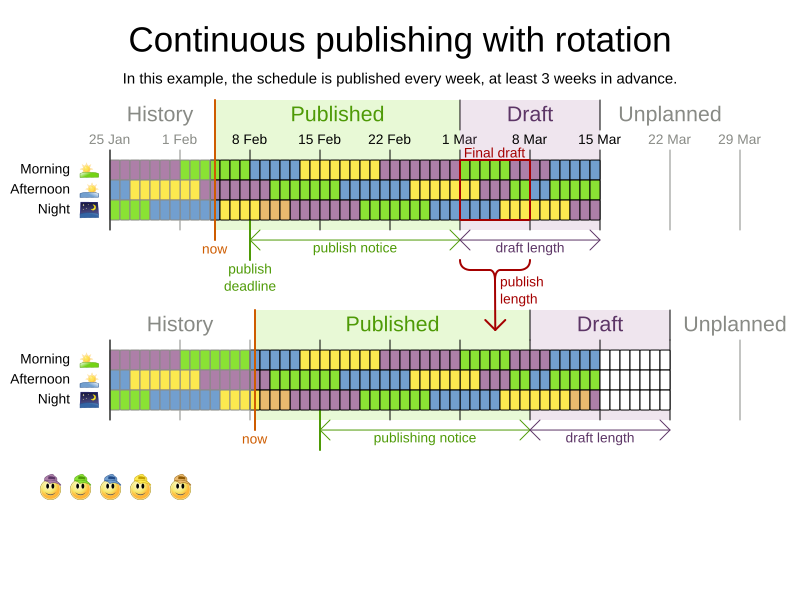
When do we solve?
-
Publish schedule weeks in advance
- Affects family/social lives
- Ad hoc changes
- Sick employees
- Shift changes

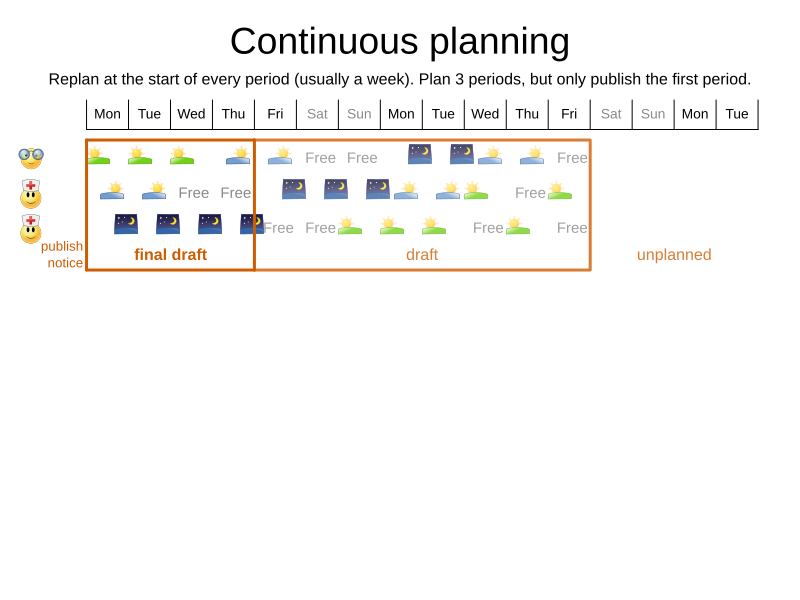
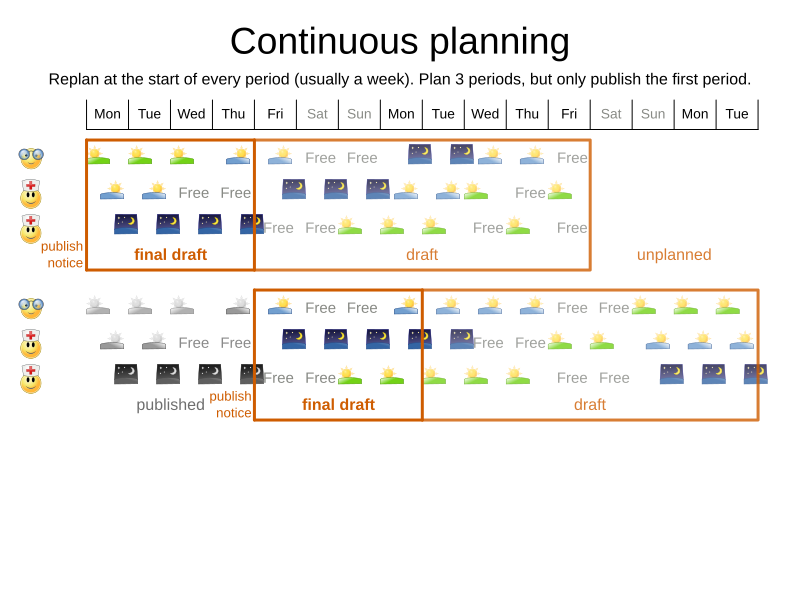
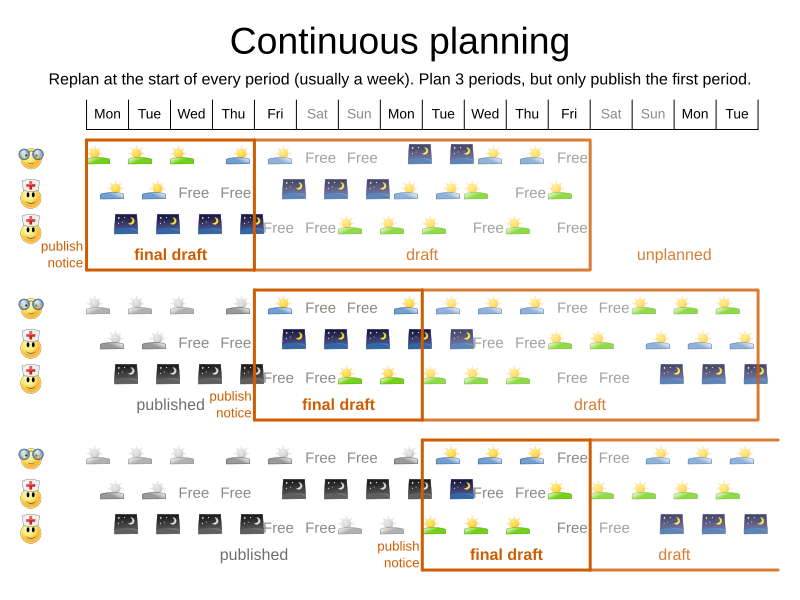
Who's in control?
The user
OptaWeb Employee Rostering (non-technical)
Press down to show
Press right to skip






Introducing
the
OptaWeb
Employee Rostering
template
OptaWeb Employee Rostering
Domain

Skill
- Examples:
- English, Spanish, ...
- Critical care, psychiatric care, ...
- First line support, second line support, ...
- Mortgages, insurances, ...
DEMO
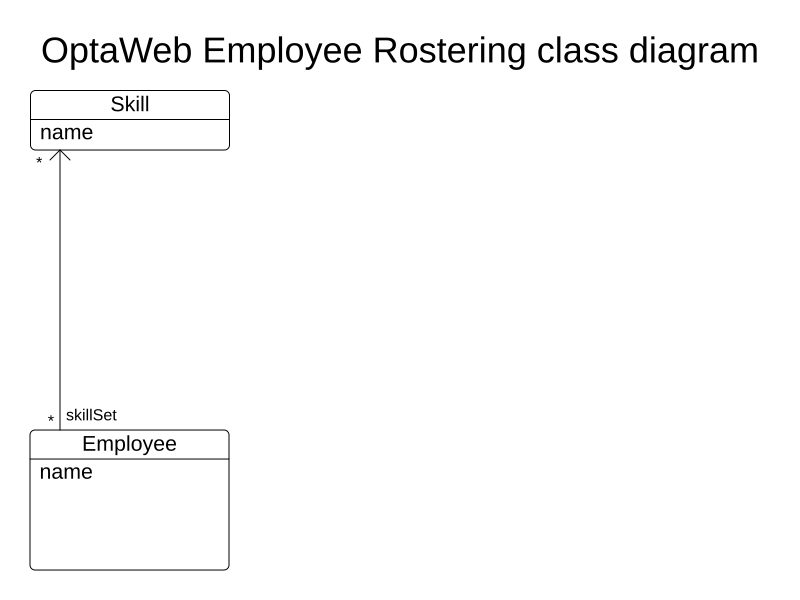
Employee
- Proficient in 0, 1 or multiple skills
- Can be assigned to shifts
DEMO
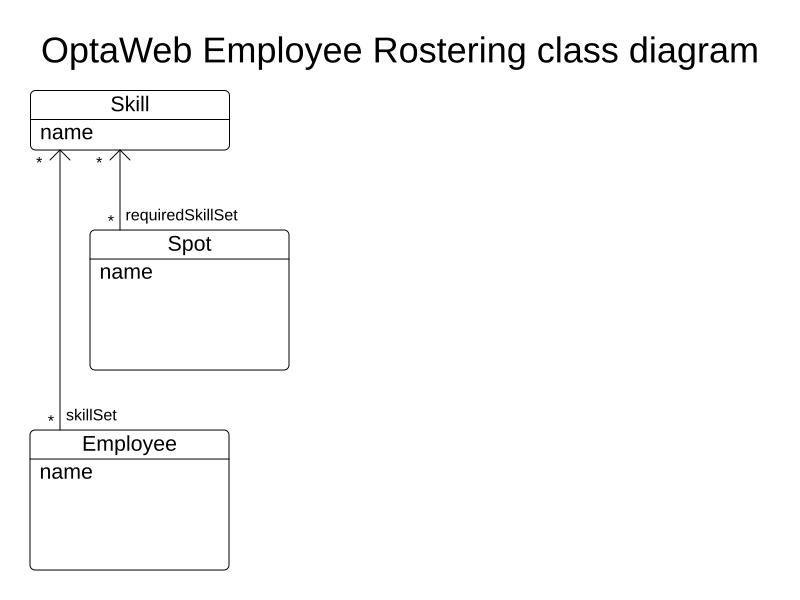
Spot
- Requires 0, 1 or multiple skills
- Examples:
- Ambulance unit 1 (requires emergency care)
- SFO north gate security (requires arms licence)
- Calls from Montreal (requires English and French)
DEMO
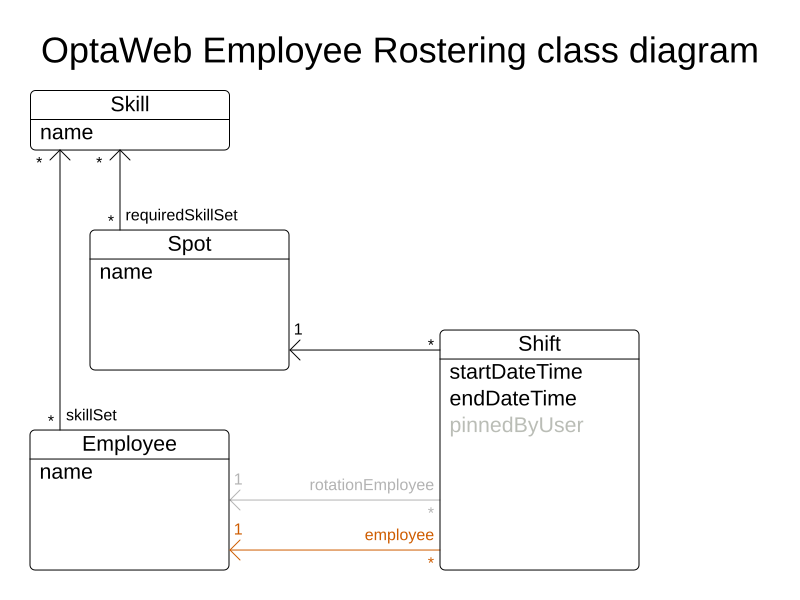
Shift
- Has a spot
- Has a starting date and time
- Has a ending date and time
- Will be assigned to an employee
- Examples:
- 1 Feb 2018: 6 AM → 2 PM @ Ambulance unit 1
- 1 Feb 2018: 2 PM → 10 PM @ Ambulance unit 1
- 1 Feb 2018: 9 AM → 5 PM @ Critical care unit
DEMO
OptaWeb Employee Rostering
Automatic shift assignment


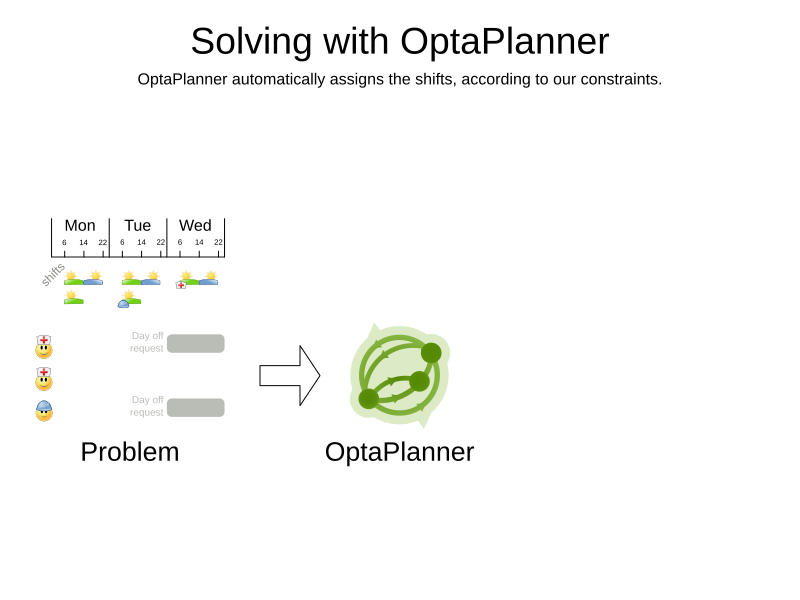
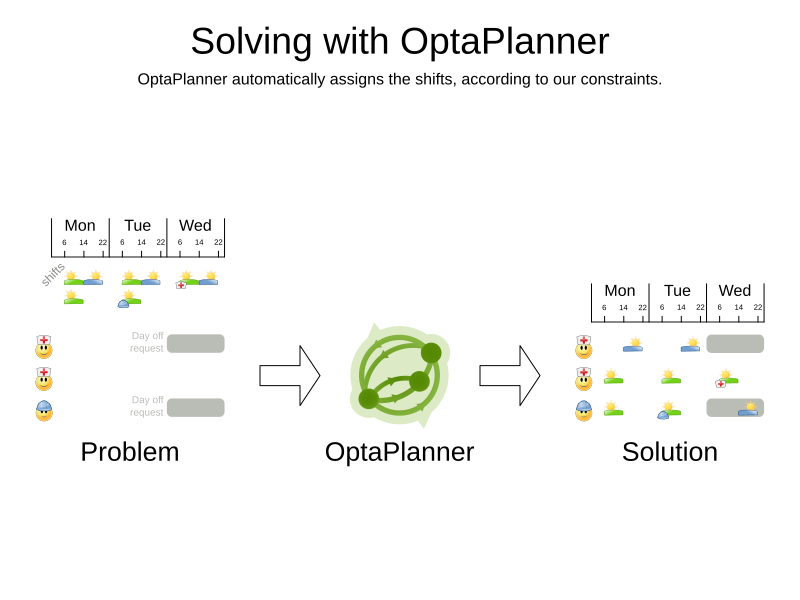
DEMO

Red Hat Build of OptaPlanner

- In production around the globe
- Full support by Red Hat
Project relation
OptaWeb
Employee Rostering
OptaPlanner
- Web application
- Docker image
- Employee rostering
- Uses OptaPlanner
- Engine
- Embeddable (jar file)
- Any constraint problem










Constraint Solving
Artificial Intelligence










Constraints
Constraints
- Skill requirements
- 2 shifts at the same time
- 10 hours between 2 shifts
- Employees on PTO
- Employees working time wishes
- ...
DEMO









Who's in control?

The user is in control
DEMO
OptaWeb Employee Rostering
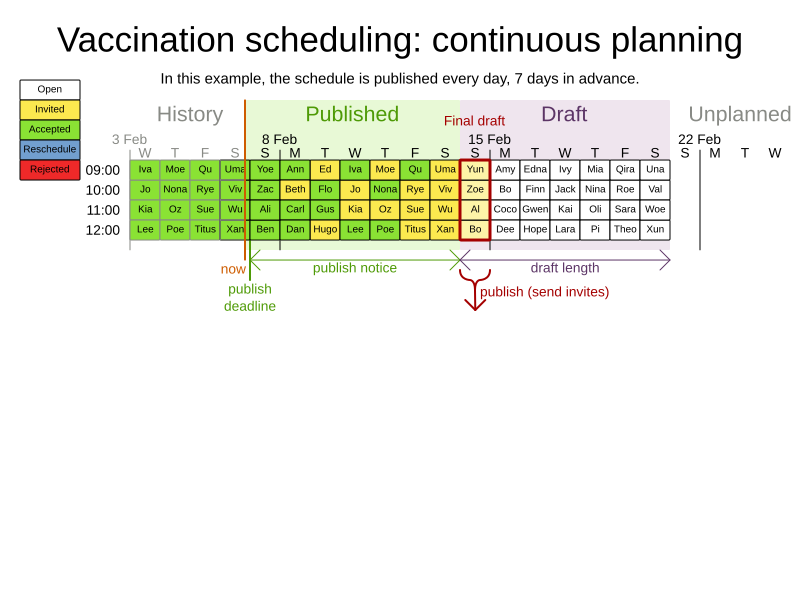
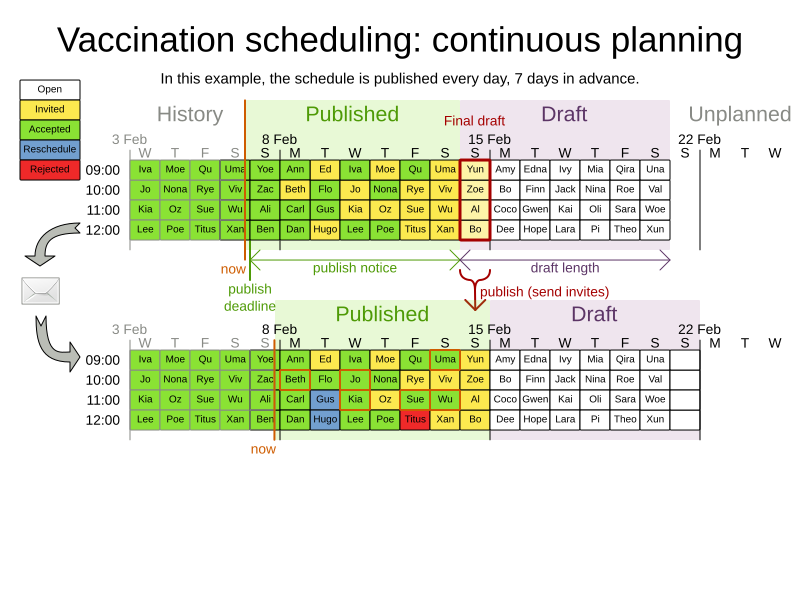
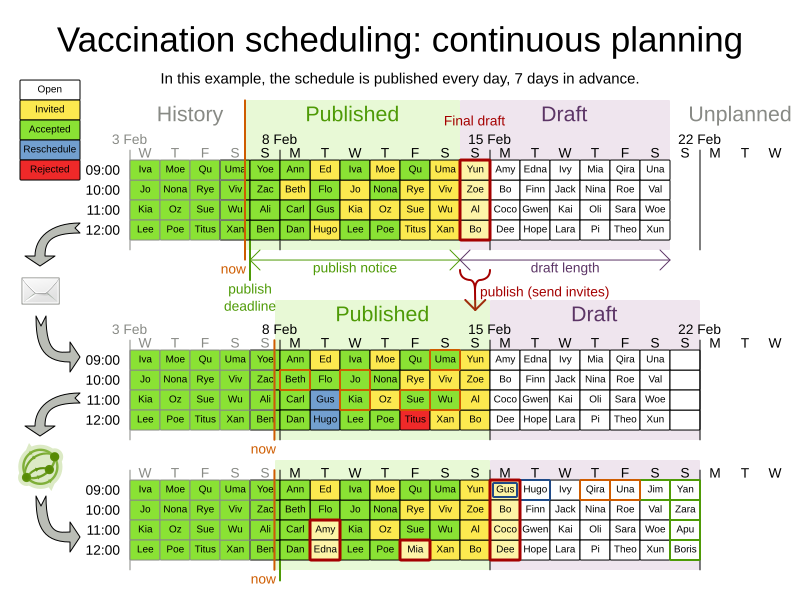
Continuous planning




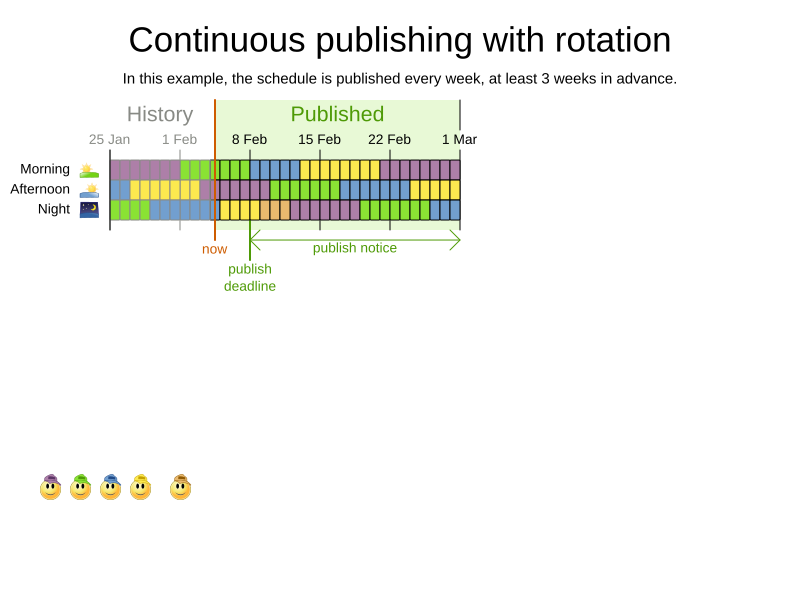
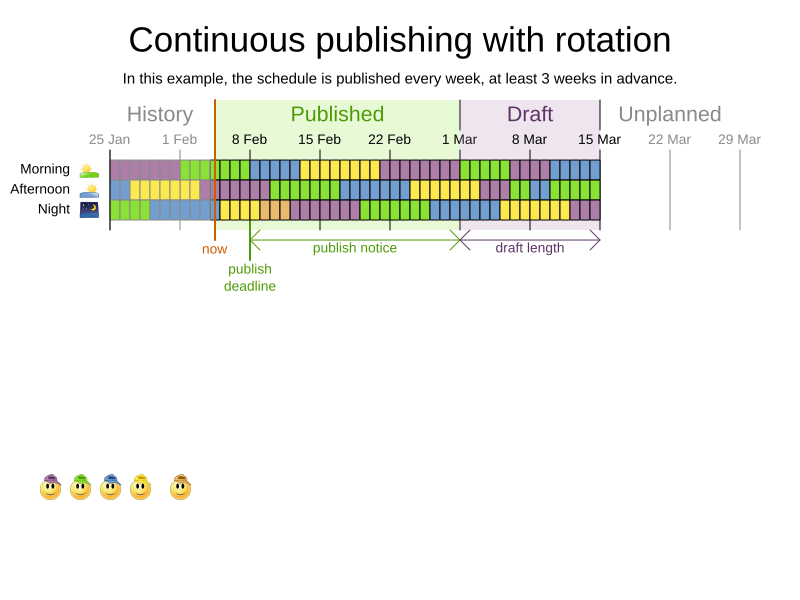
OptaWeb Employee Rostering
Publishing





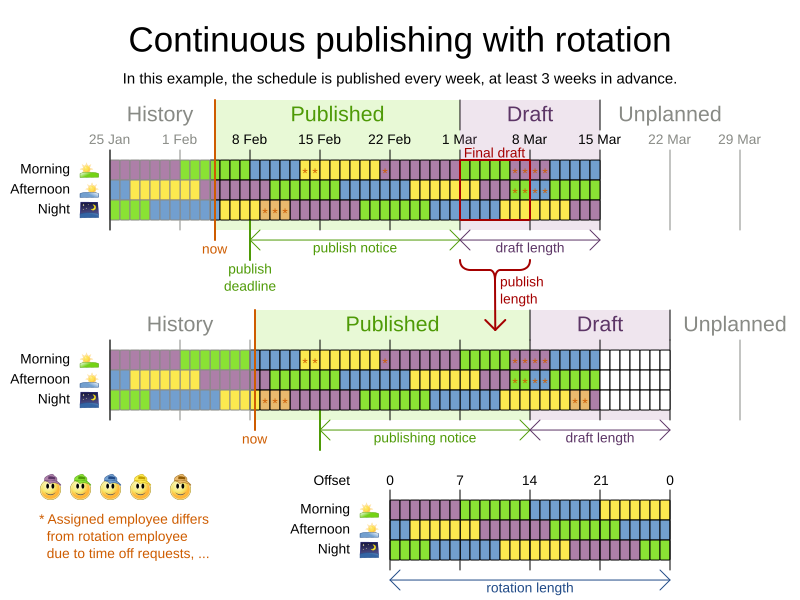
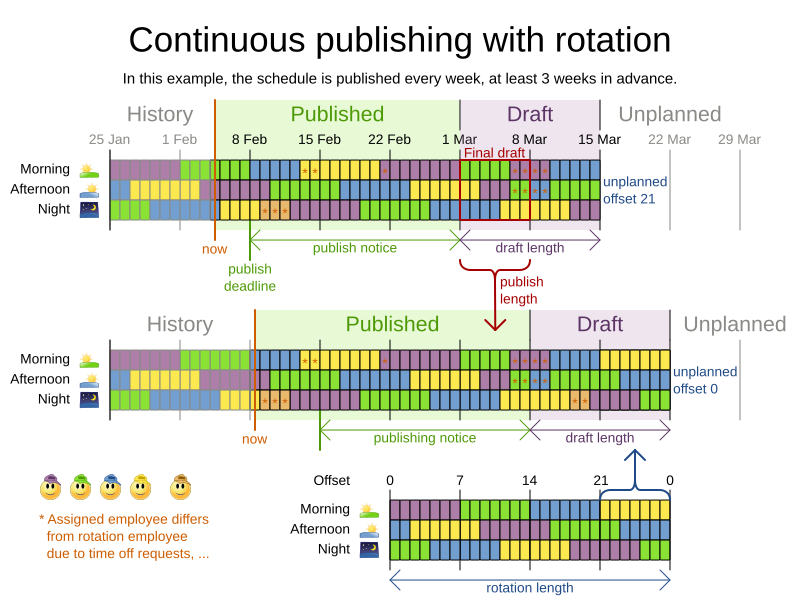
Rotation



DEMO

Roadmap
Changes after publication
Ann is sick, Beth needs to go funeral, ...
- "Reserve" spots
-
Non-disruptive replanning:
- Propose new schedule with minimal impact on published shifts
- Start contacting them immediately
Simulation
What if ...
- that maternity nurse quits?
- we hire 2 unskilled employees?
We can now measure the impact.
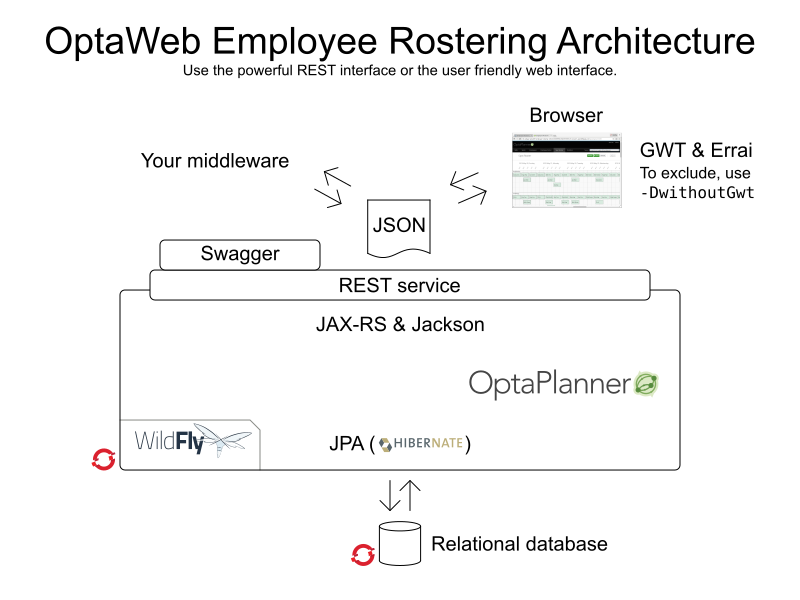
Under the hood

REST service
DEMO
Getting started
Build from source
to OpenShift Dedicated
$ git clone https://github.com/kiegroup/optaweb-employee-rostering.git
...
$ cd optaweb-employee-rostering
$ oc login https://api.YOUR_SERVER.openshift.com
...
$ ./provision.sh setup
...Build from source
to WildFly
$ git clone https://github.com/kiegroup/optaweb-employee-rostering.git
...
$ cd optaweb-employee-rostering
$ mvn clean install -DskipTests
...
// Deploy optaweb-employee-rostering-webapp-*.warTask assigning
Press down to show
Press right to skip
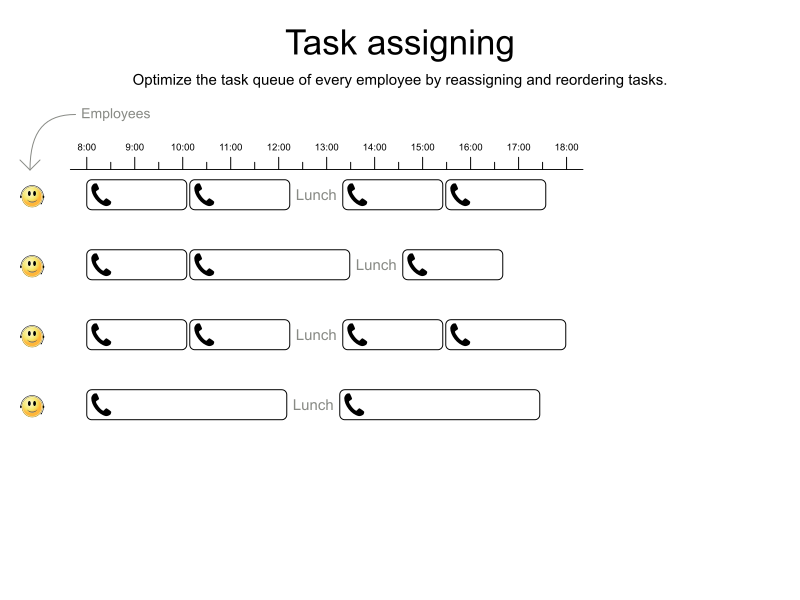
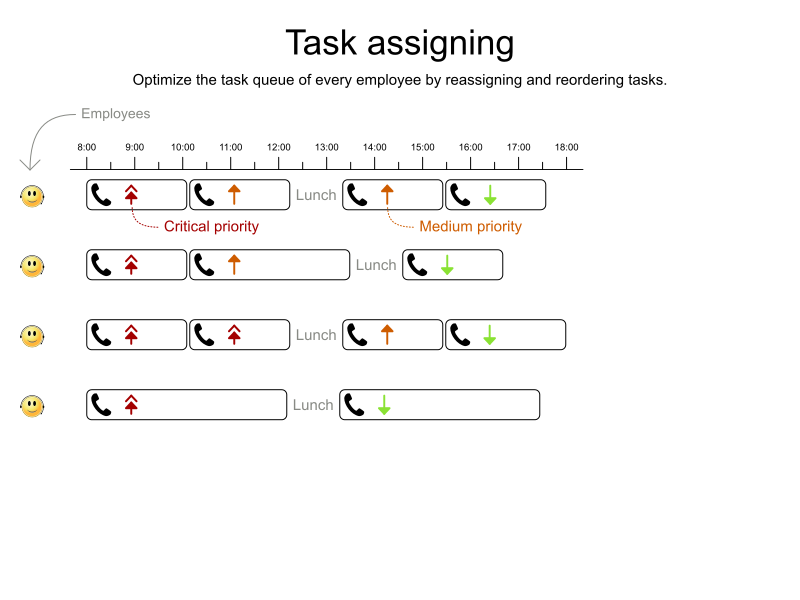
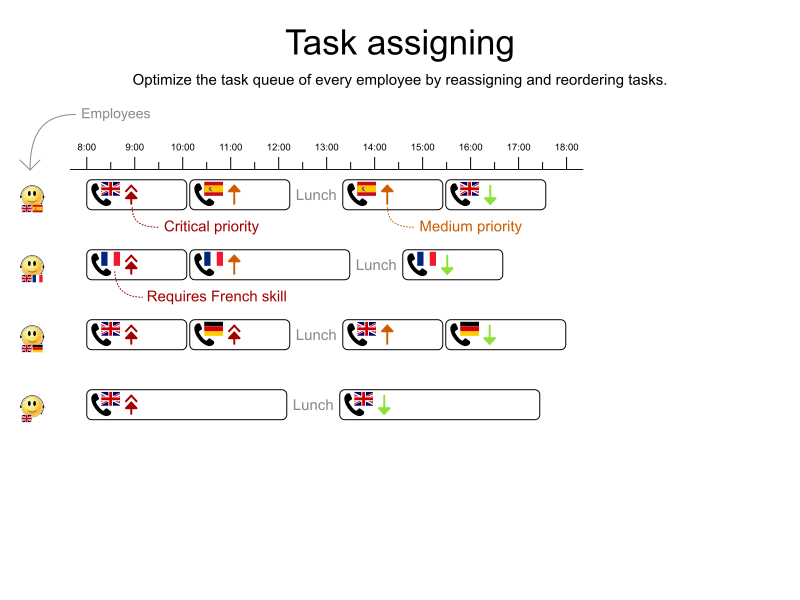
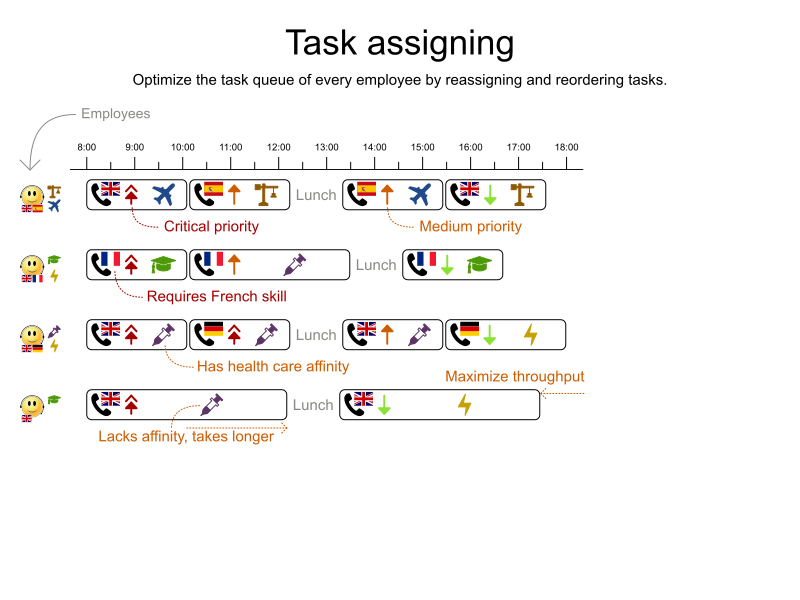
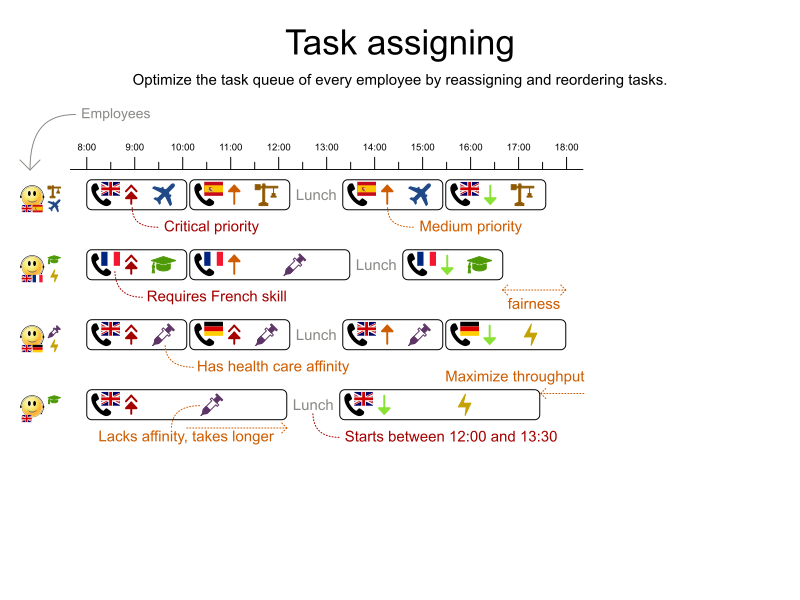
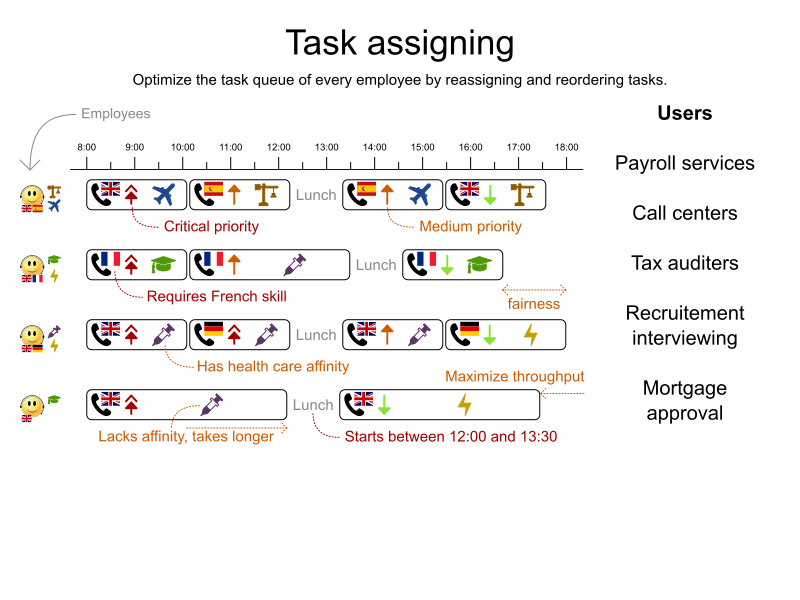
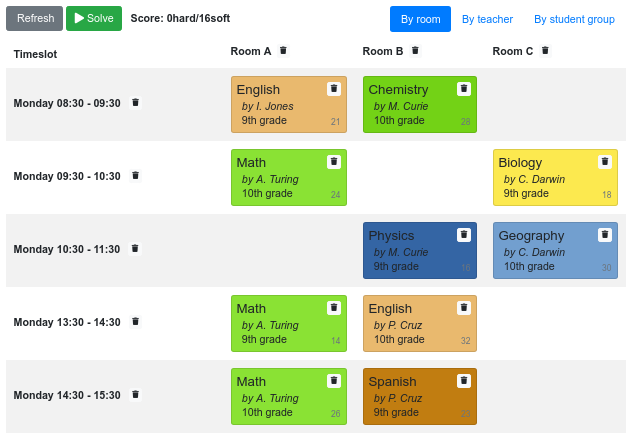
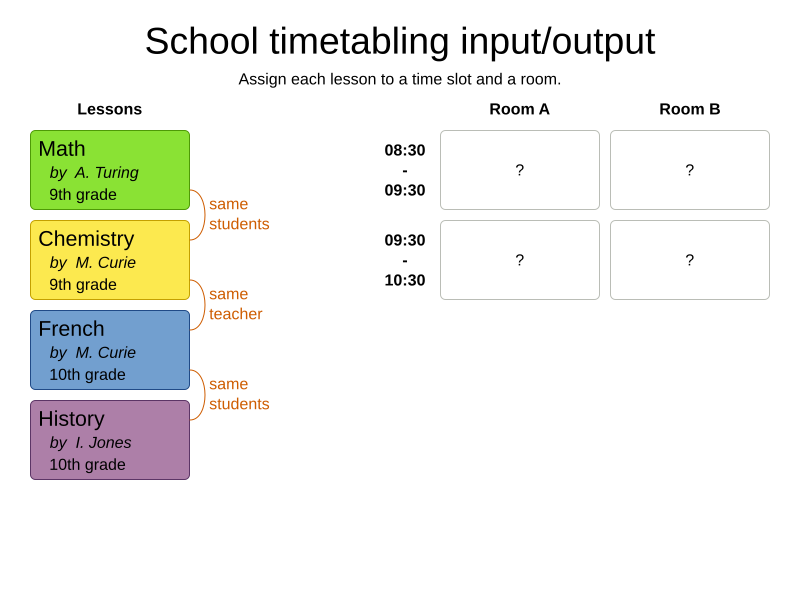
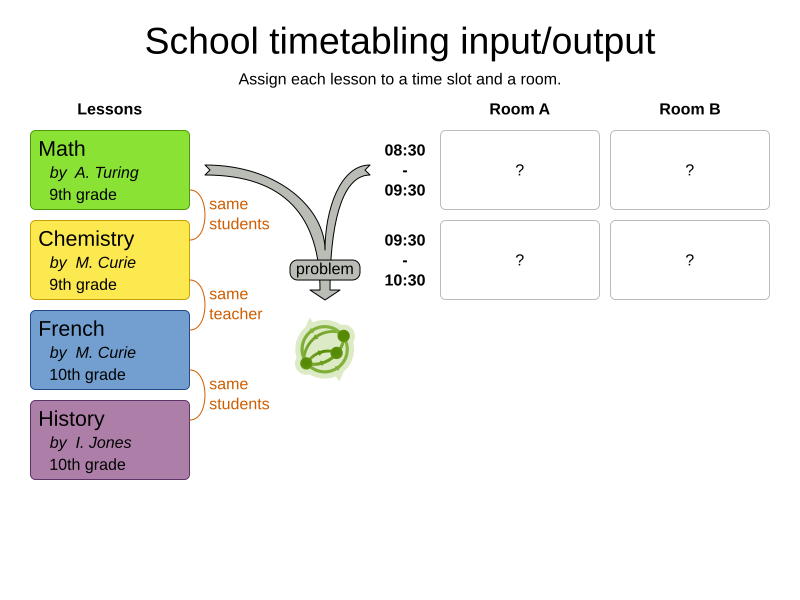
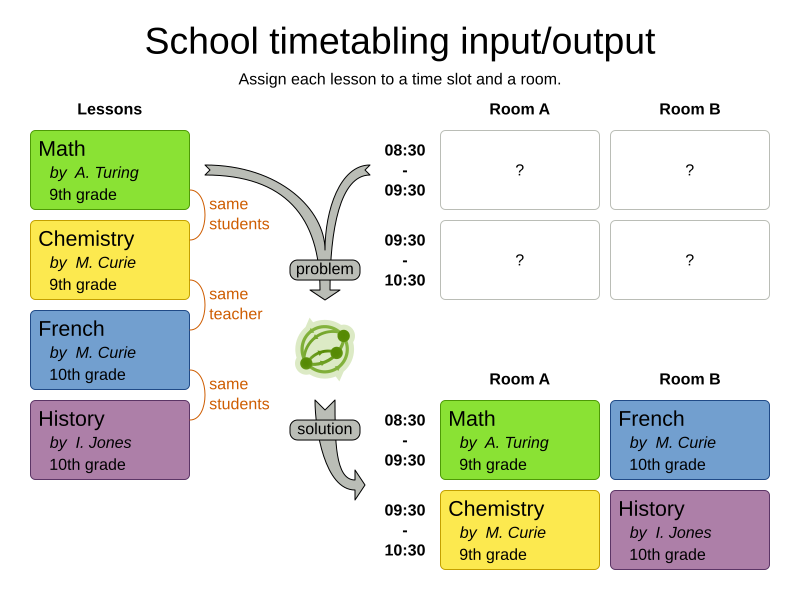
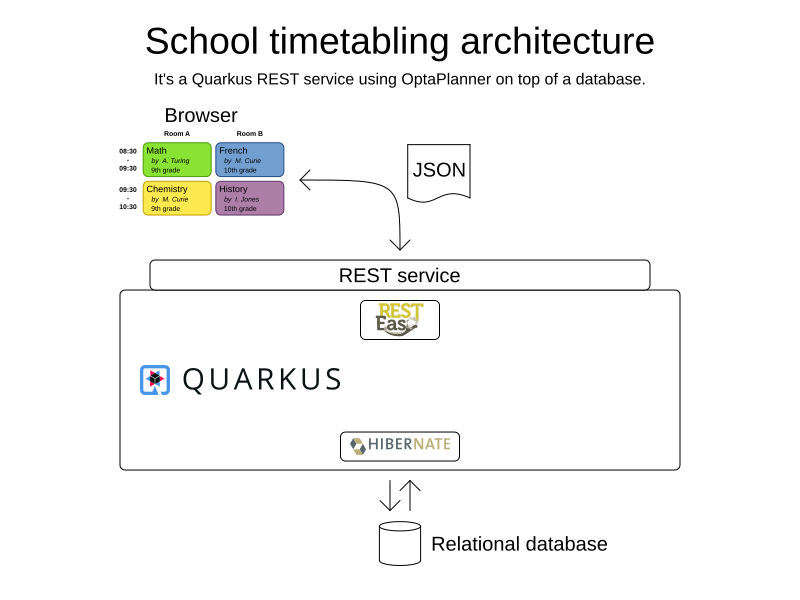
School timetabling on Quarkus
Press down to show
Press right to skip





Other planning problems?





Vehicle routing case study
Expected: -1% driving time
Result: -25% driving time
⇒ -10 million kg CO² emission per year
⇒ -100 million $ cost per year
And many more
- Maintenance scheduling (grids, equipment, ...)
- Agenda scheduling (court hearings, TV adds, ...)
- Job shop scheduling
- Task assignment
- ...
The world is full
of planning problems

open source AI constraint solver


supersonic
subatomic
Java
or Kotlin

code.quarkus.io
Generate
pom.xml
or build.gradle
Domain

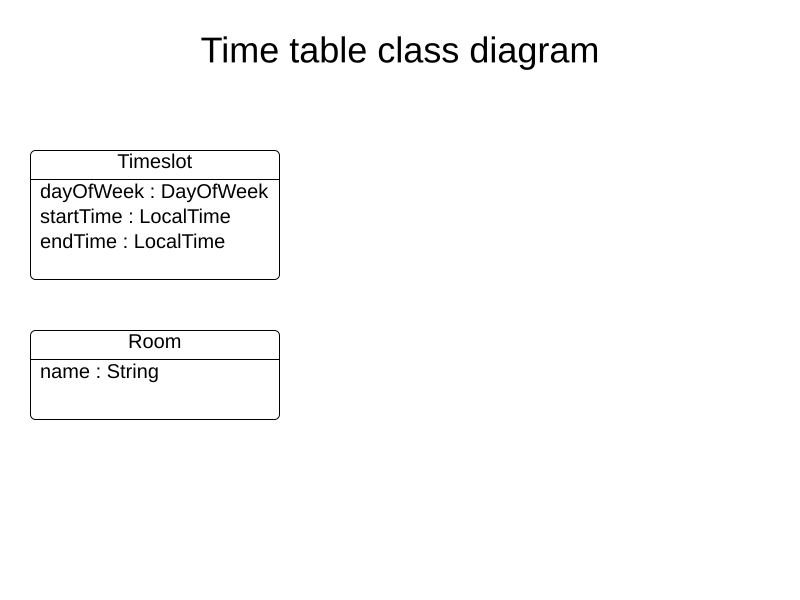
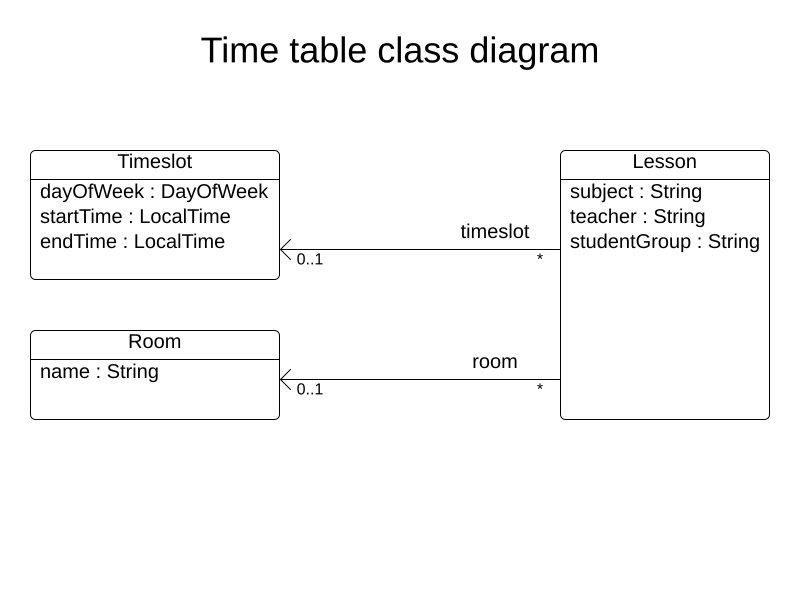
Coding
mvn quarkus:dev
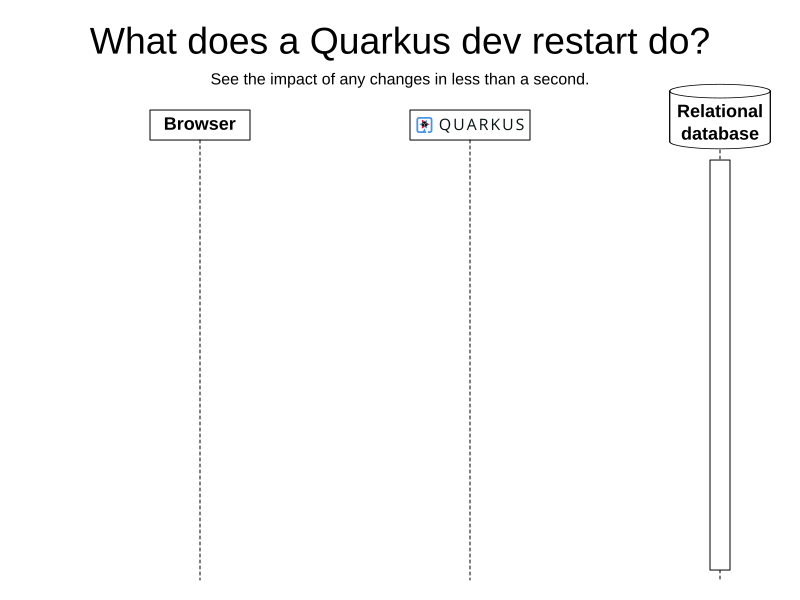
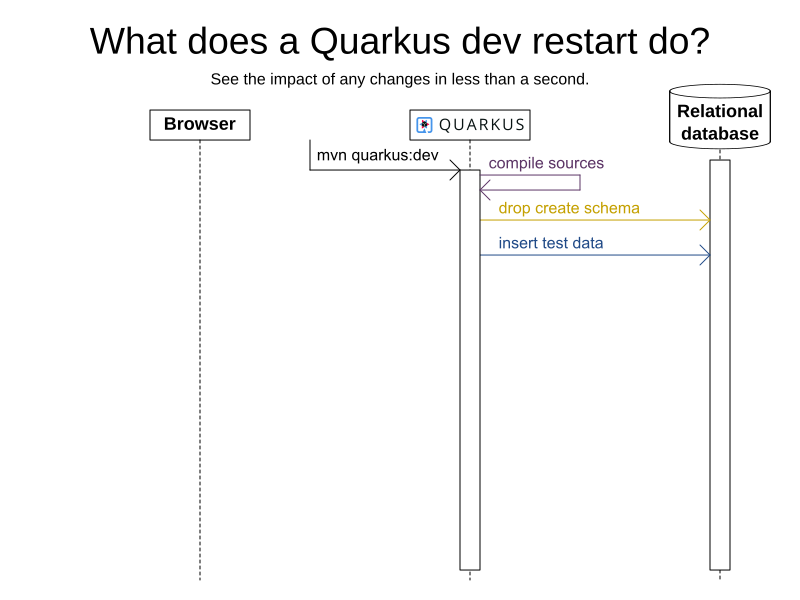
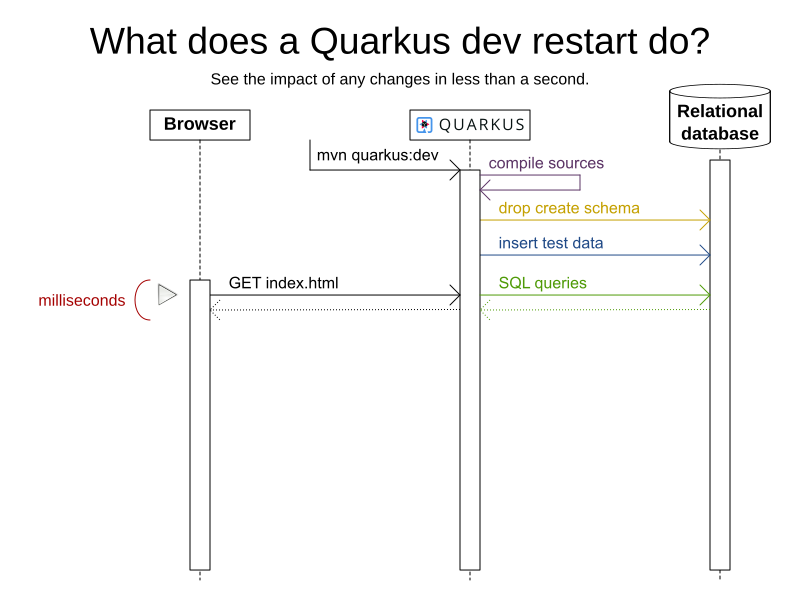
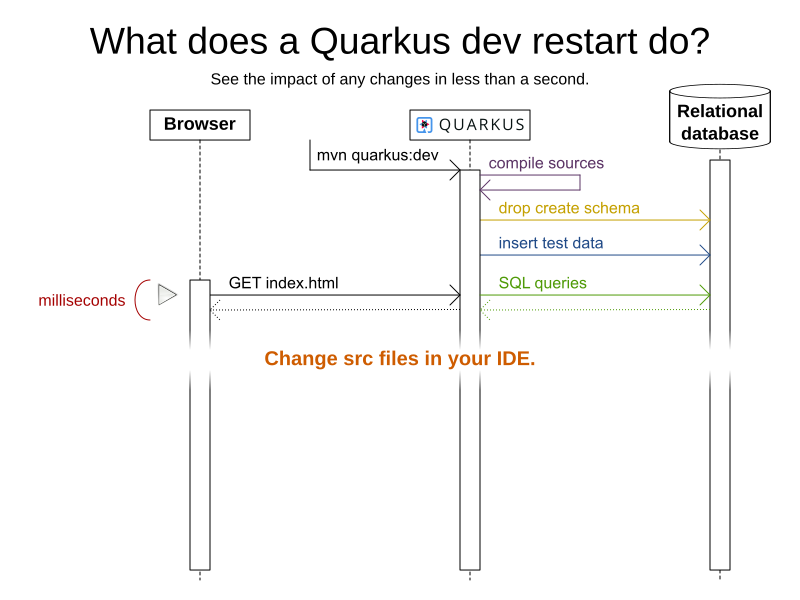
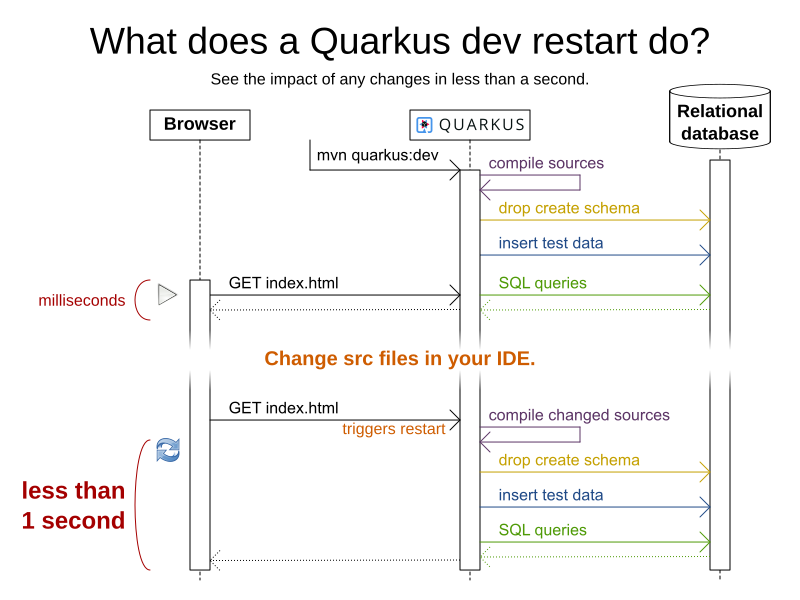
UI in JavaScript
OK...


Coding a UI in JavaScript?
Not in public
AI planning optimization

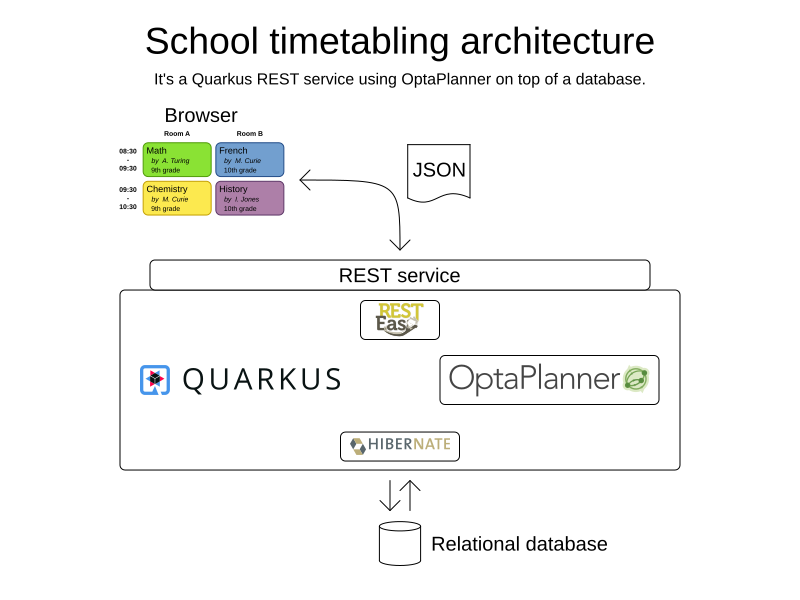

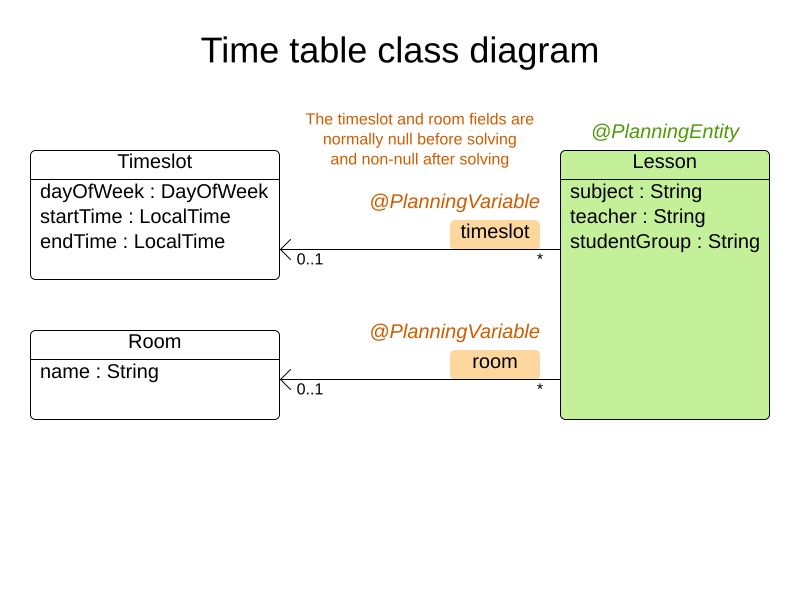
Constraints
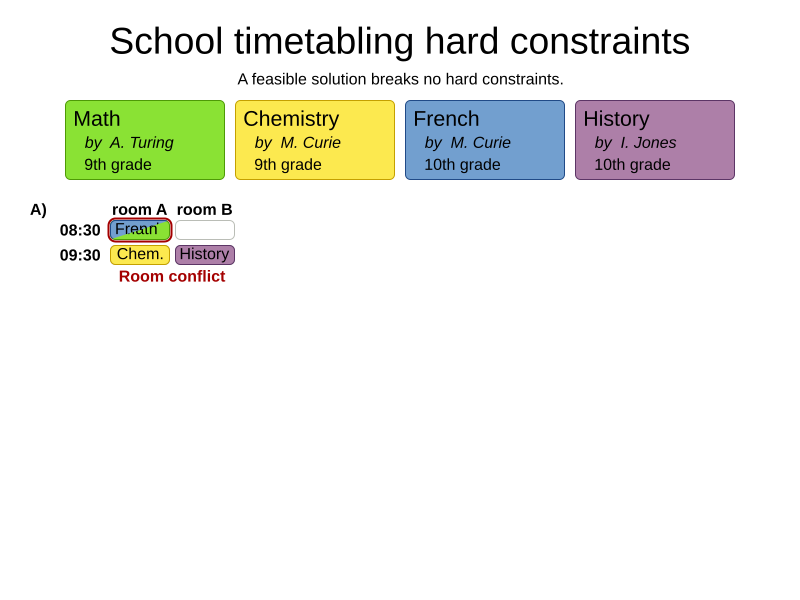
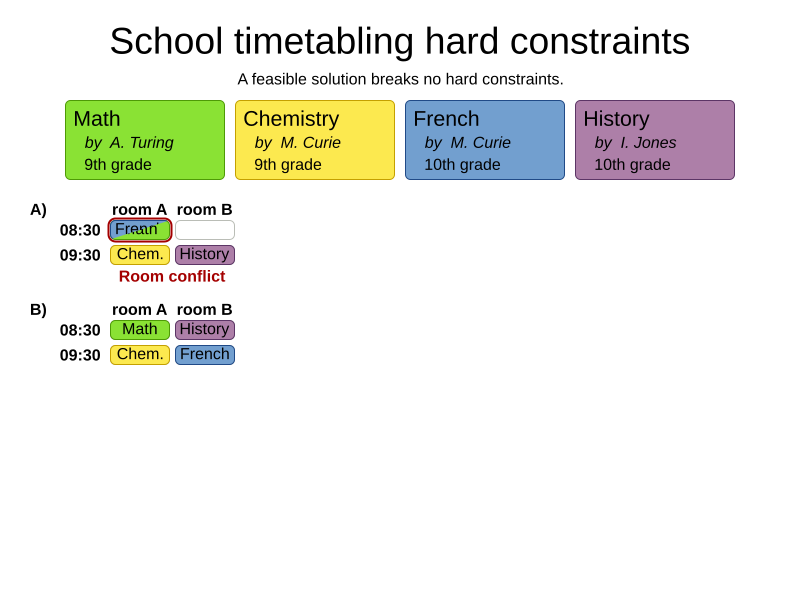
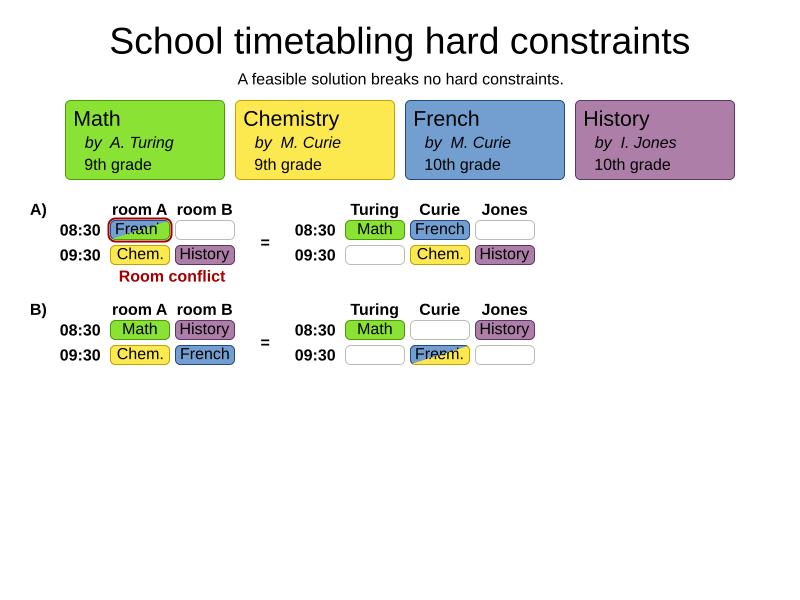
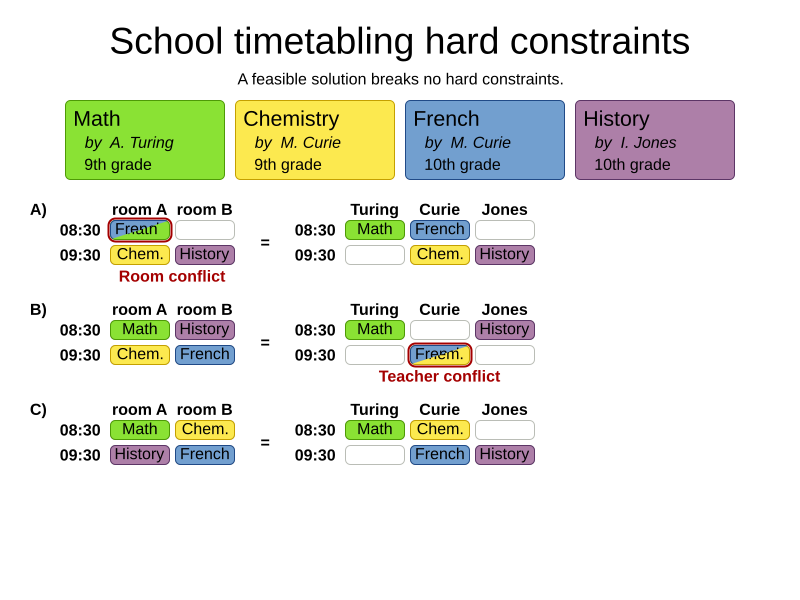
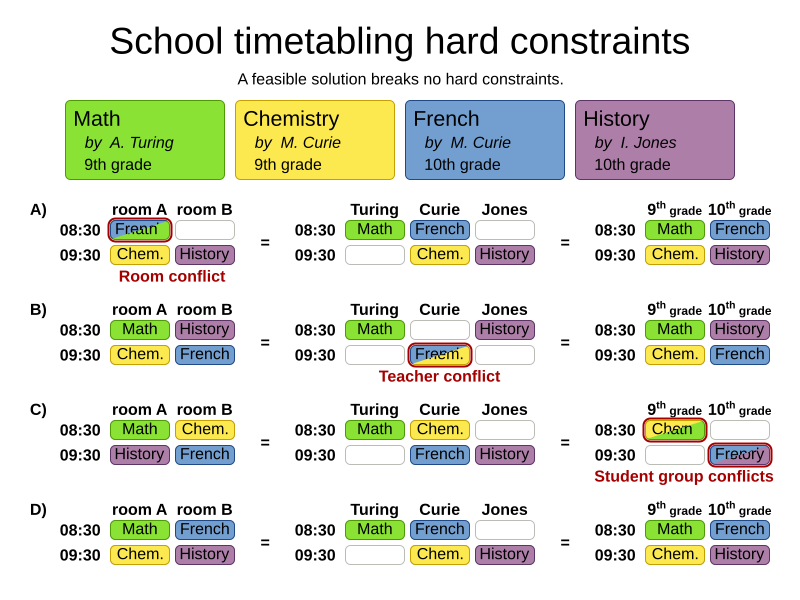
Hard and soft constraints
- Hard constraints: must not be broken
- Soft constraints: avoid being broken
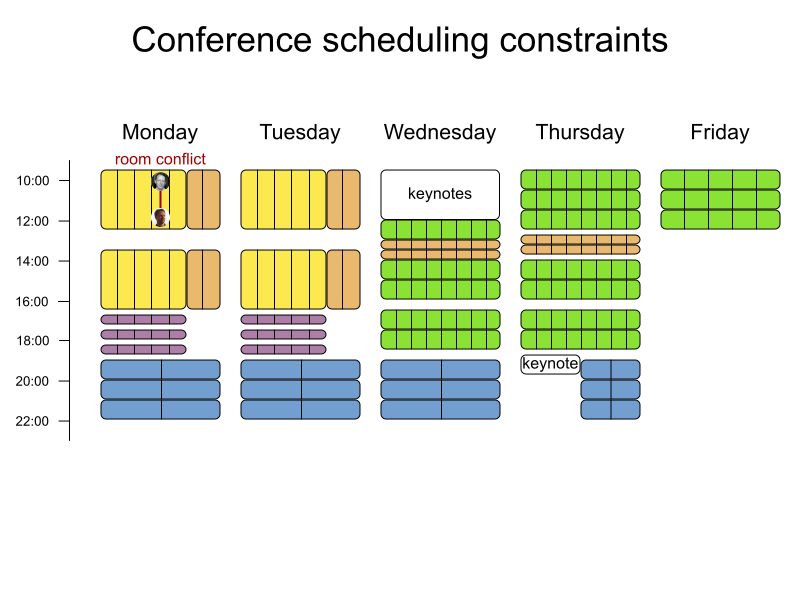
Room conflict constraint
int hardScore = 0;
for (Lesson a : lessonList) {
for (Lesson b : lessonList) {
if (a.getTimeslot() == b.getTimeslot()
&& a.getRoom() == b.getRoom()) {
hardScore--;
}
}
}
...
return HardSoftScore.ofHard(hardScore);Not incremental!
When the room of the Math lesson changes,
it checks again
if French and Chemistry use the same room.


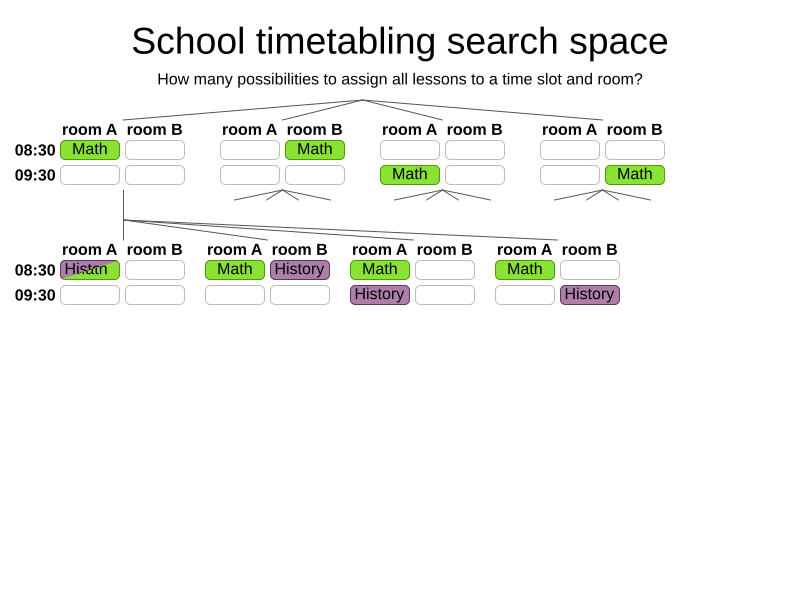
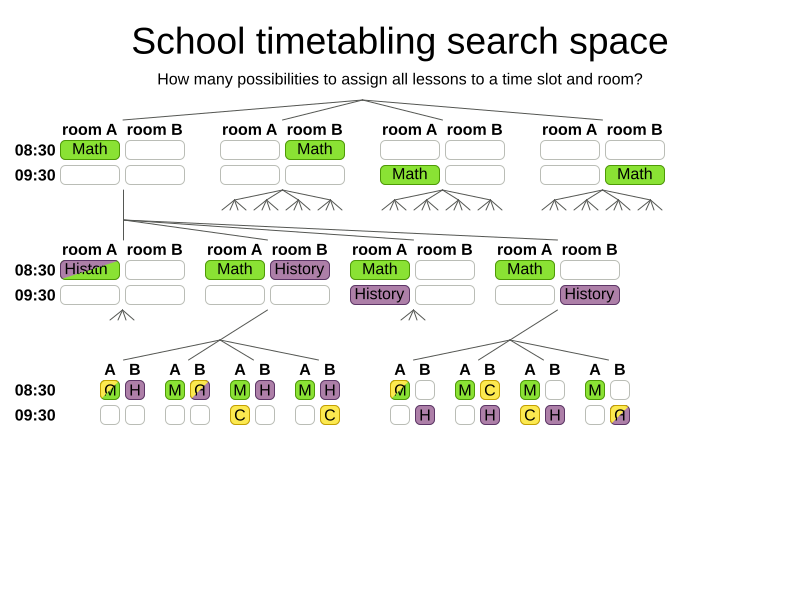
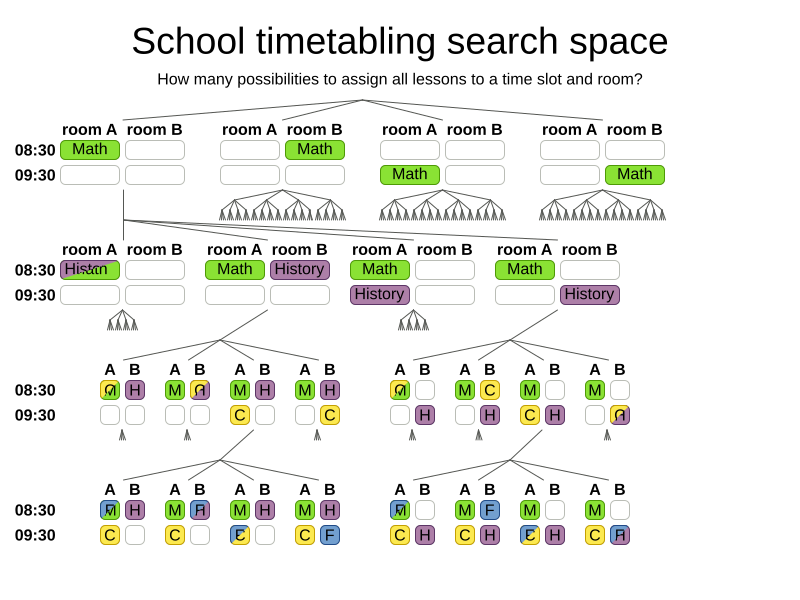
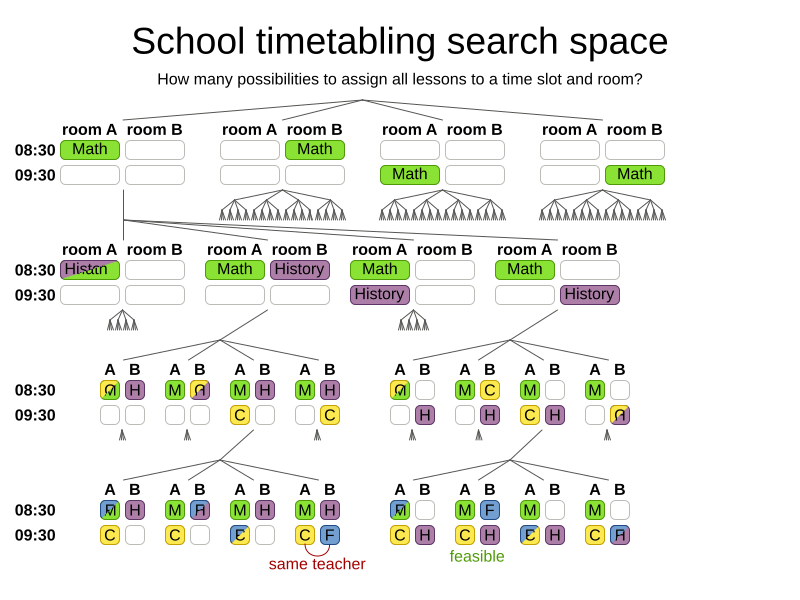
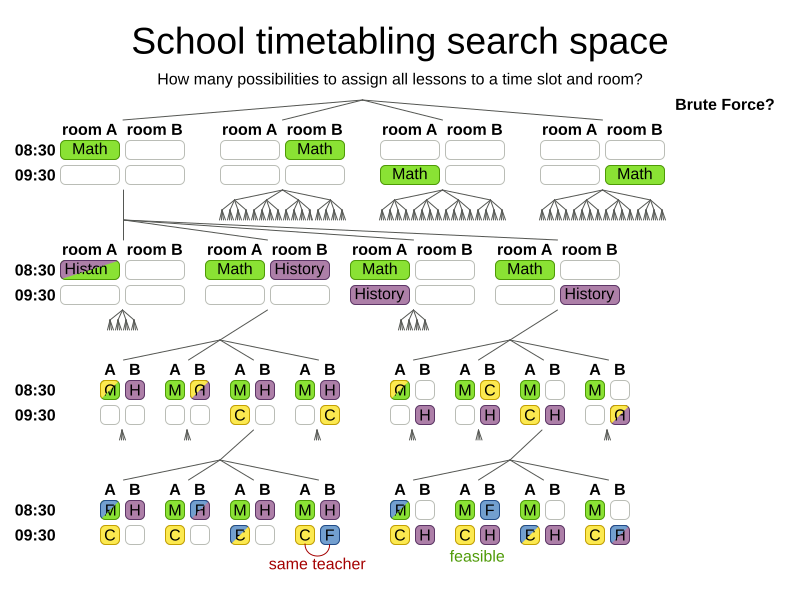
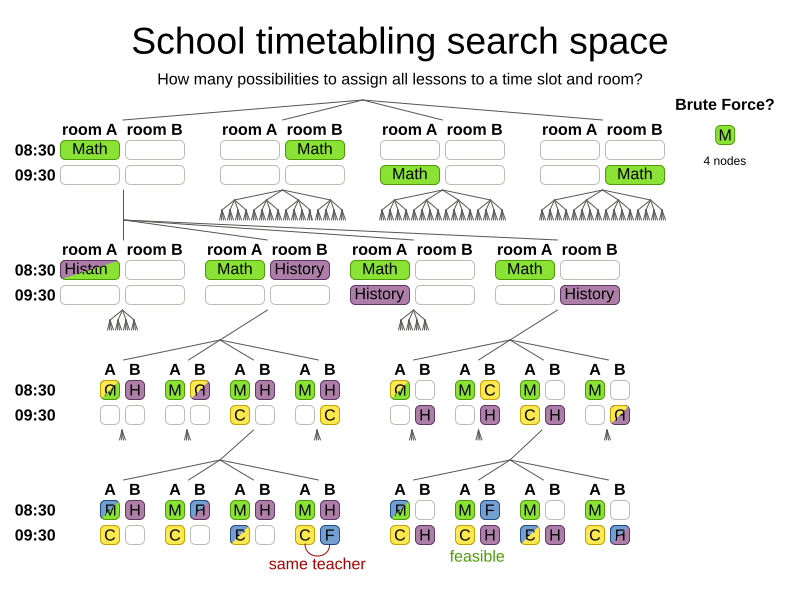
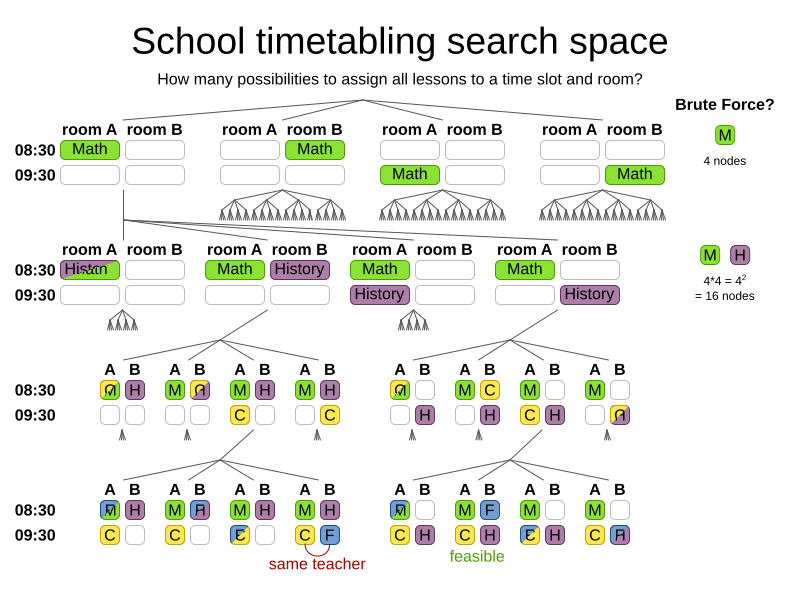
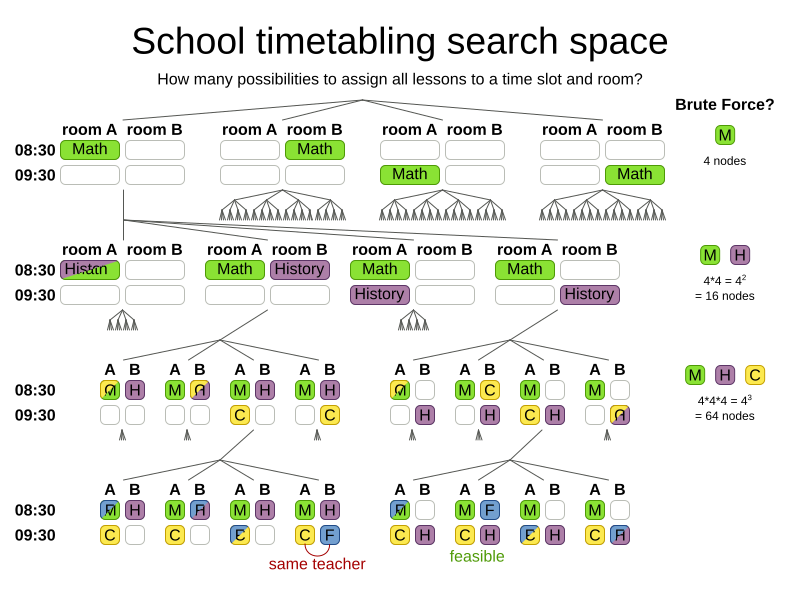
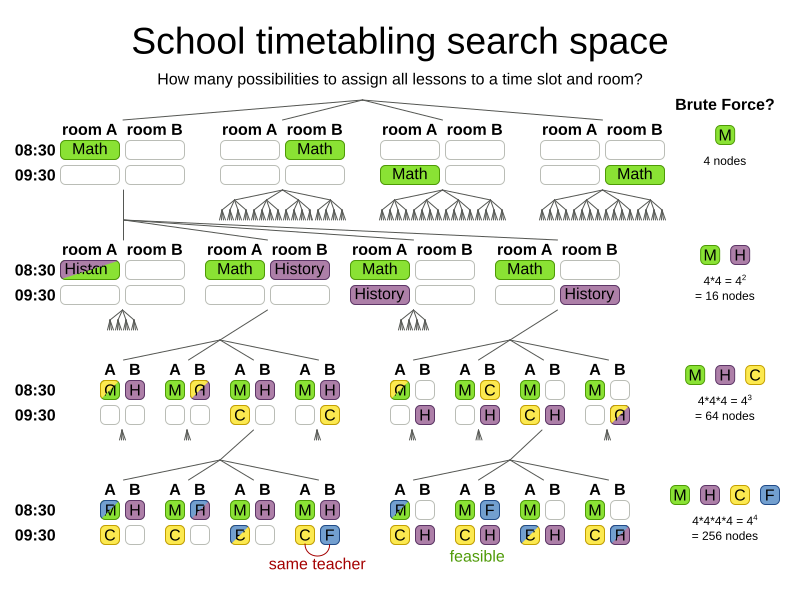
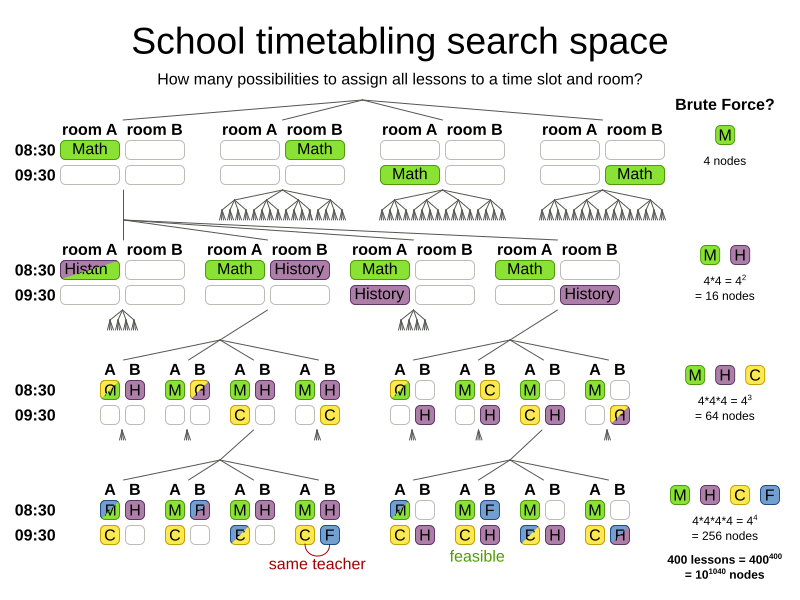
How big is the search space?
Search space for n lessons: nn
Search space for 400 lessons: 101040
Atoms in observable universe: 1080

Greedy algorithms


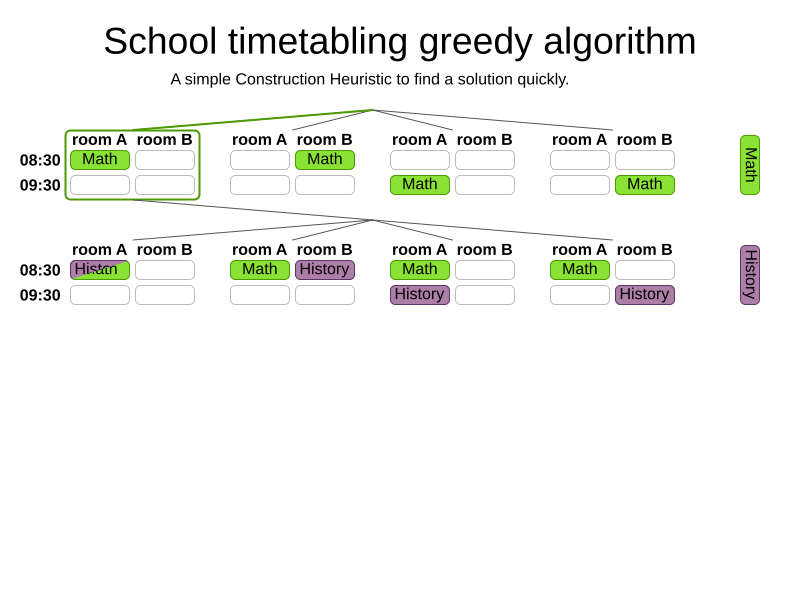
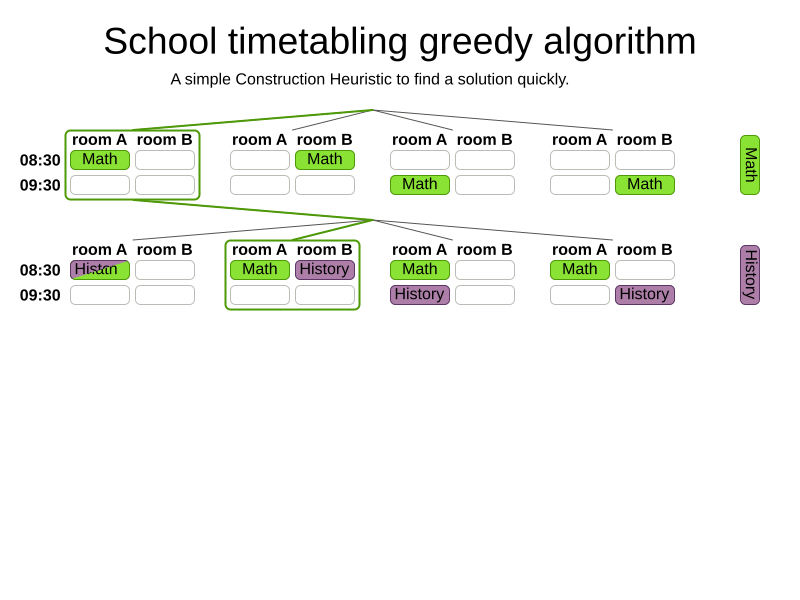
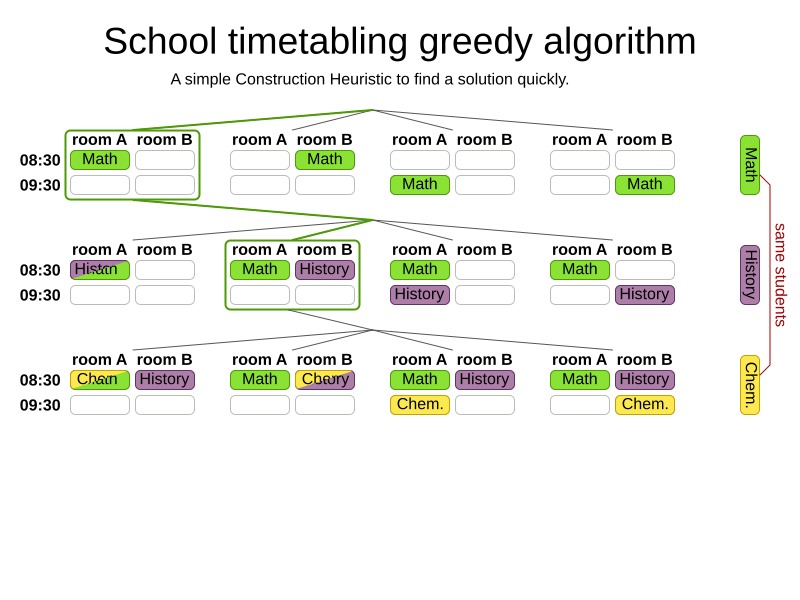
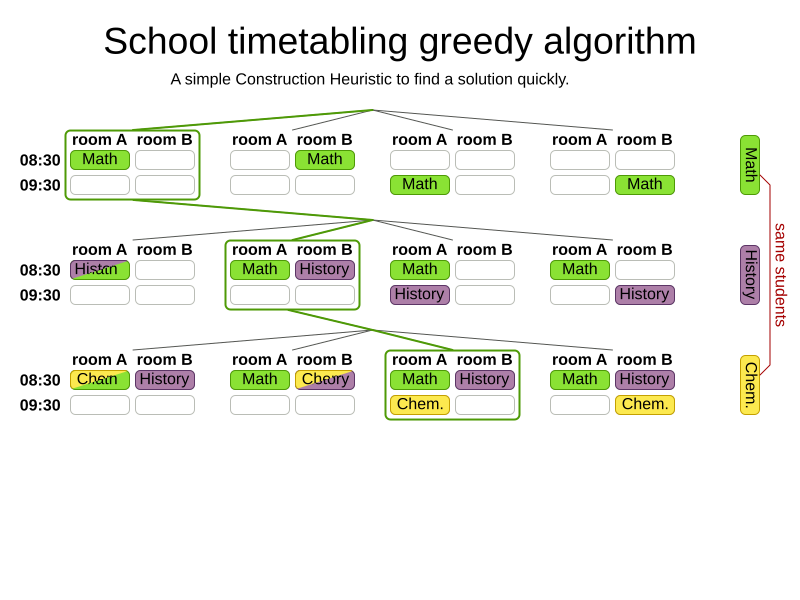
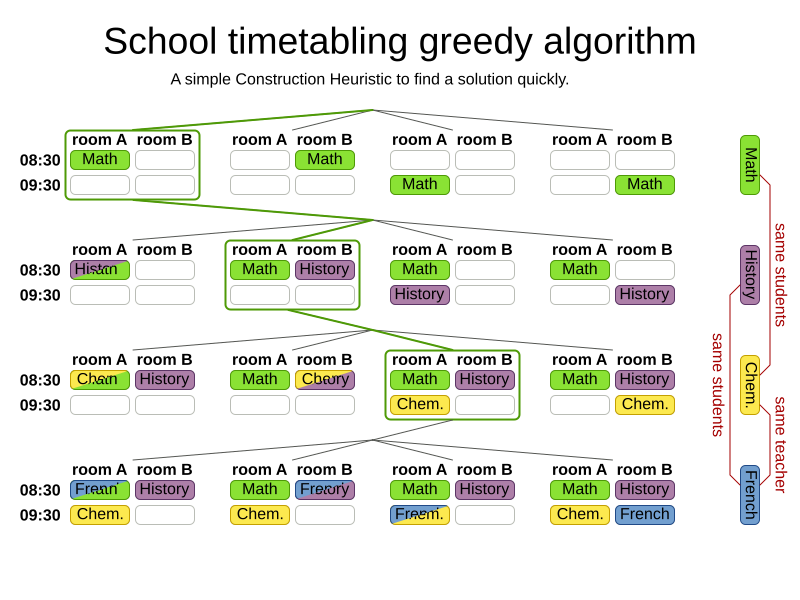
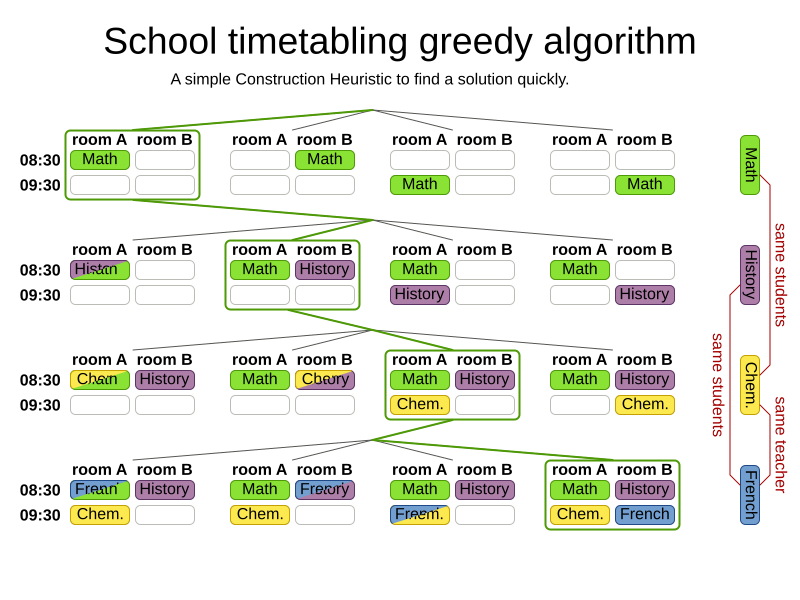

Advanced algorithms
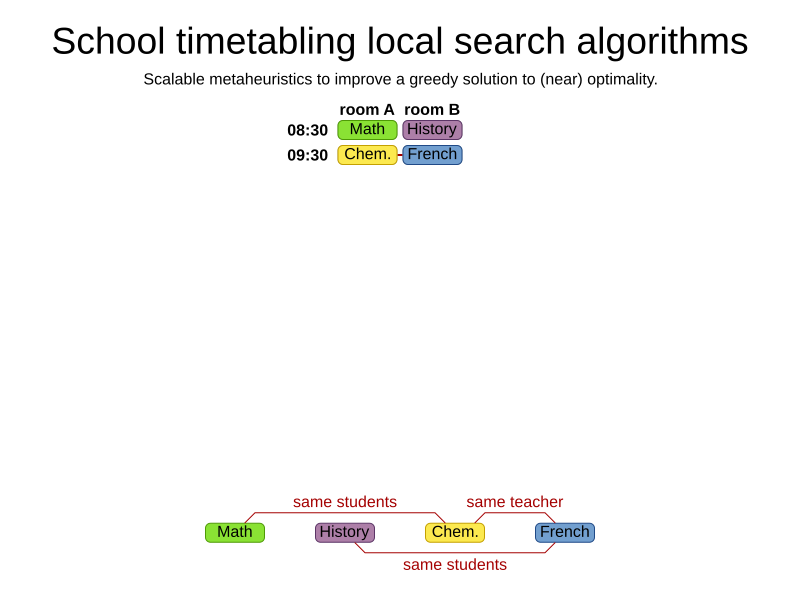
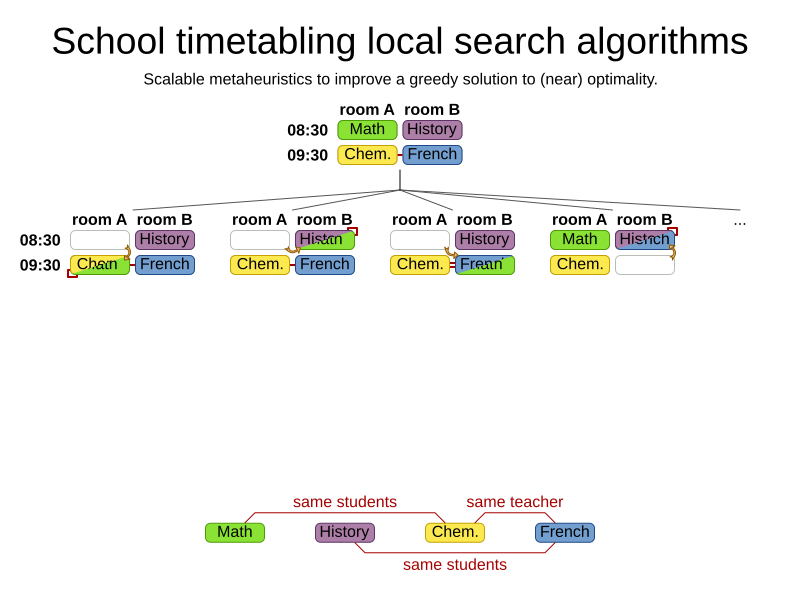
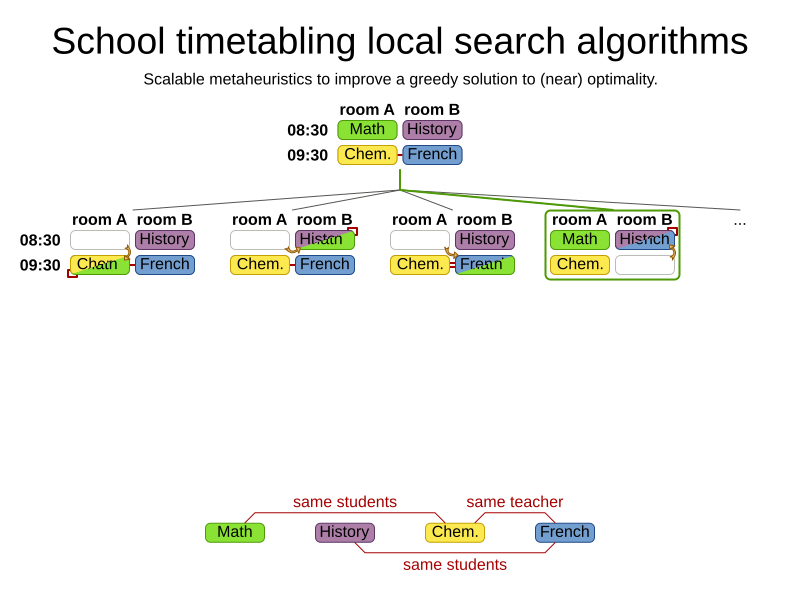
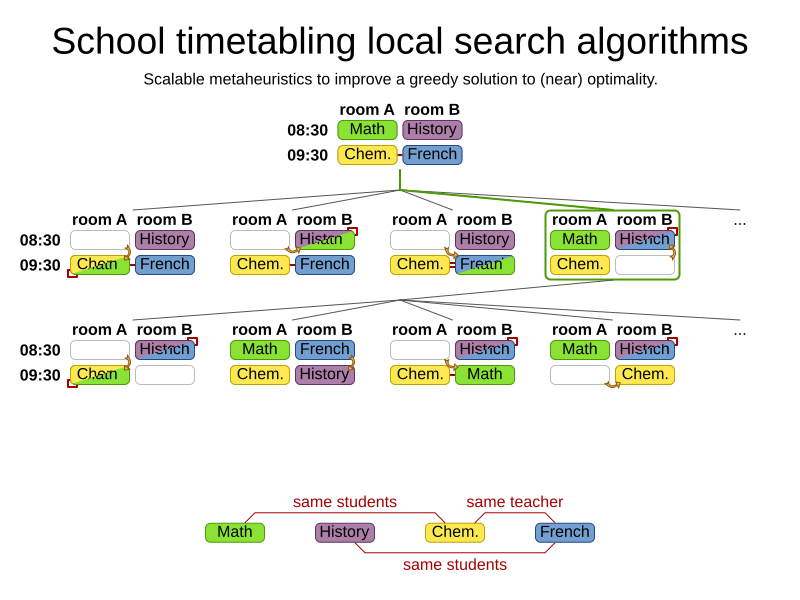
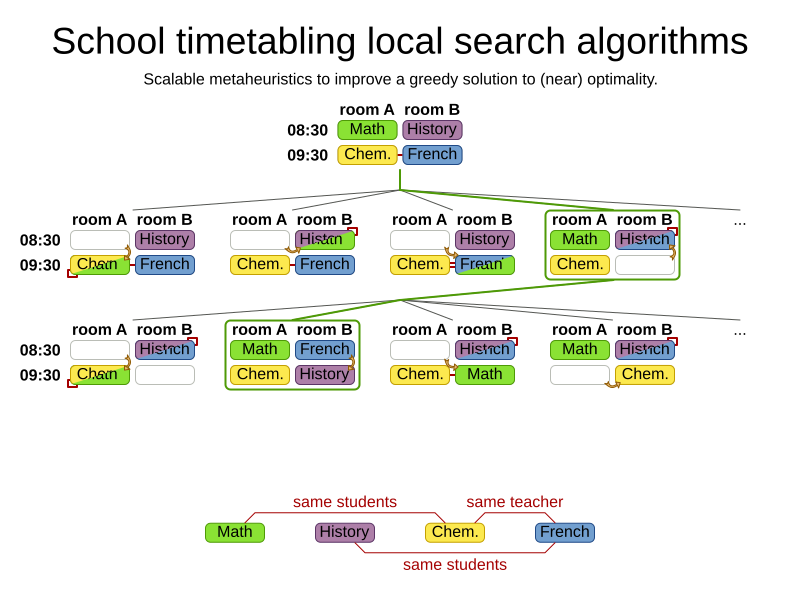
The world is full
of planning problems

open source AI constraint solver
Apache License






School timetabling on Spring Boot
Press down to show
Press right to skip










Fast forward


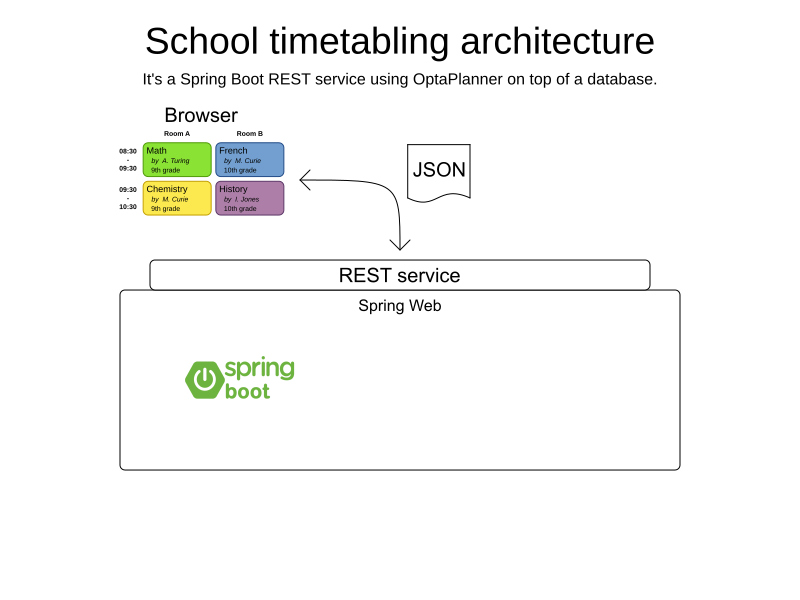
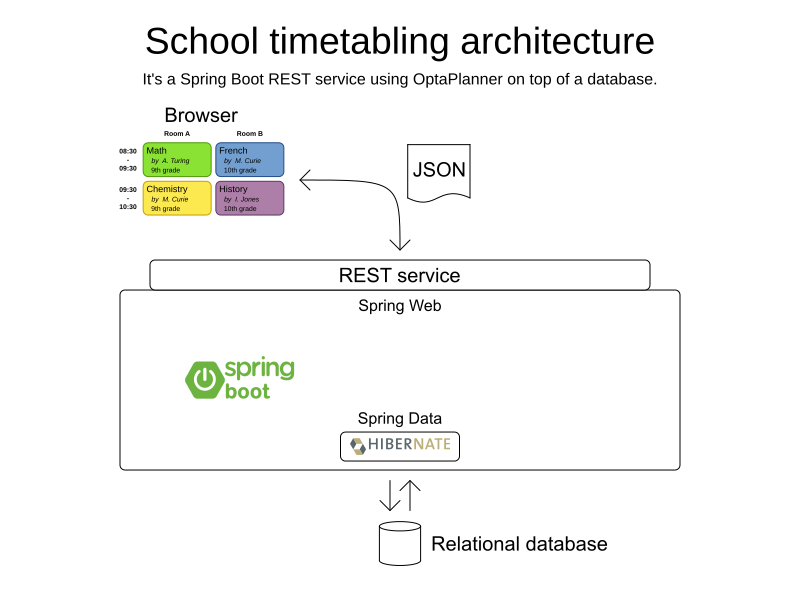
Domain


AI planning optimization

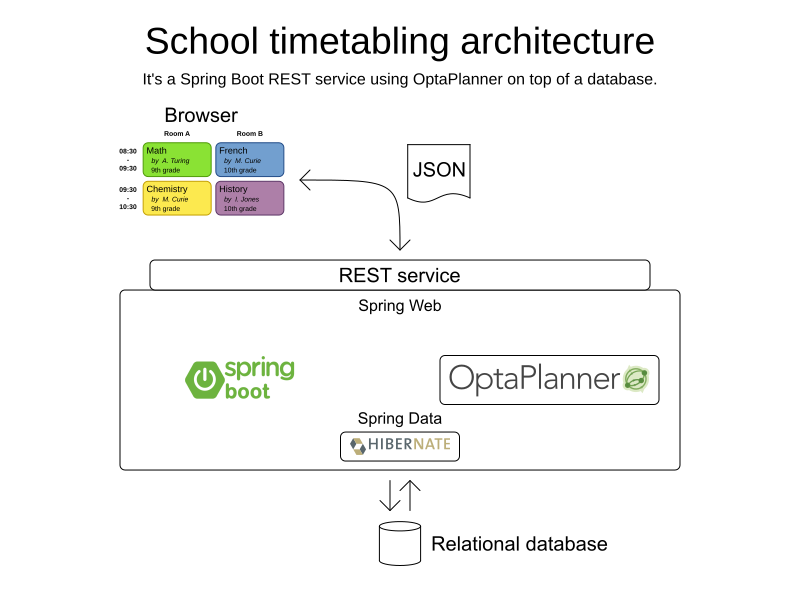


Constraints
Hard and soft constraints
- Hard constraints: must not be broken
- Soft constraints: avoid being broken
COVID-19 constraint
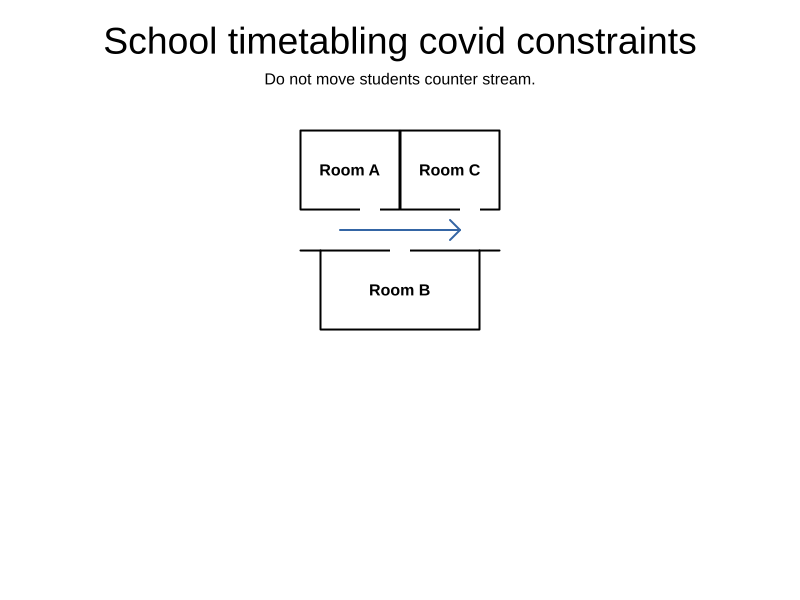
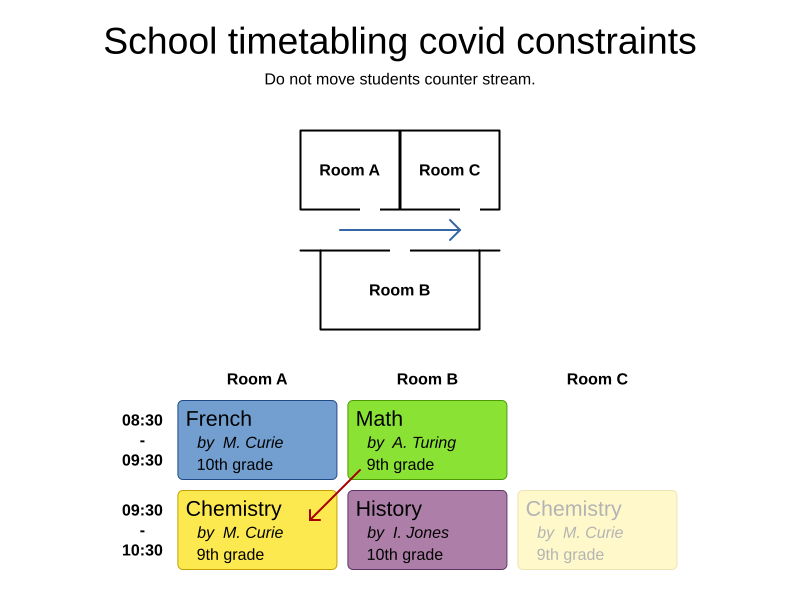
COVID-19 constraint
protected Constraint roomCounterStream(ConstraintFactory f) {
return f
.forEach(Lesson.class)
.join(Lesson.class,
Joiners.equal(Lesson::getStudentGroup),
Joiners.equal(
(lesson) -> lesson.getTimeslot().getDayOfWeek()),
Joiners.equal(
(lesson1) -> lesson1.getTimeslot().getEndTime(),
(lesson2) -> lesson2.getTimeslot().getStartTime()),
// Students transfer counter stream.
// For example from room C to room B.
Joiners.greaterThan(
(lesson) -> lesson.getRoom().getName()))
.penalize("Room counter stream",
HardSoftScore.ONE_HARD);
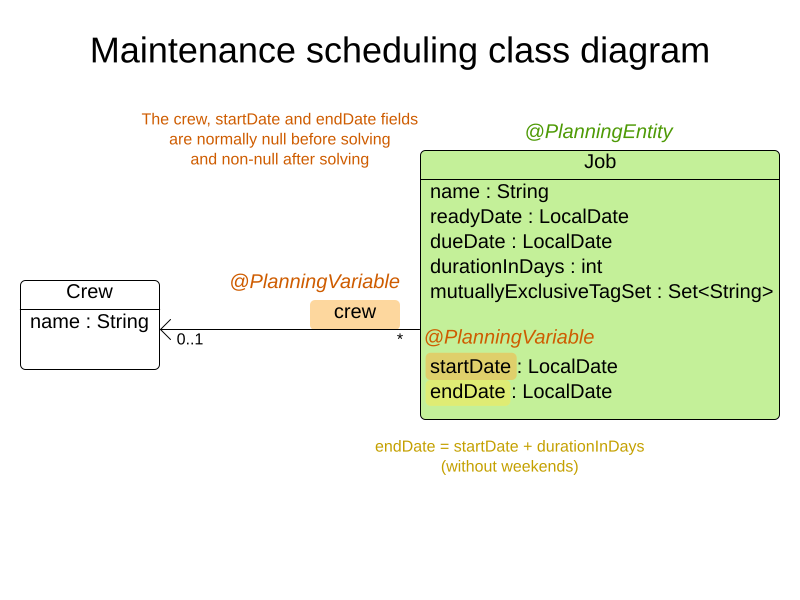
}Maintenance scheduling on Quarkus
Press down to show
Press right to skip
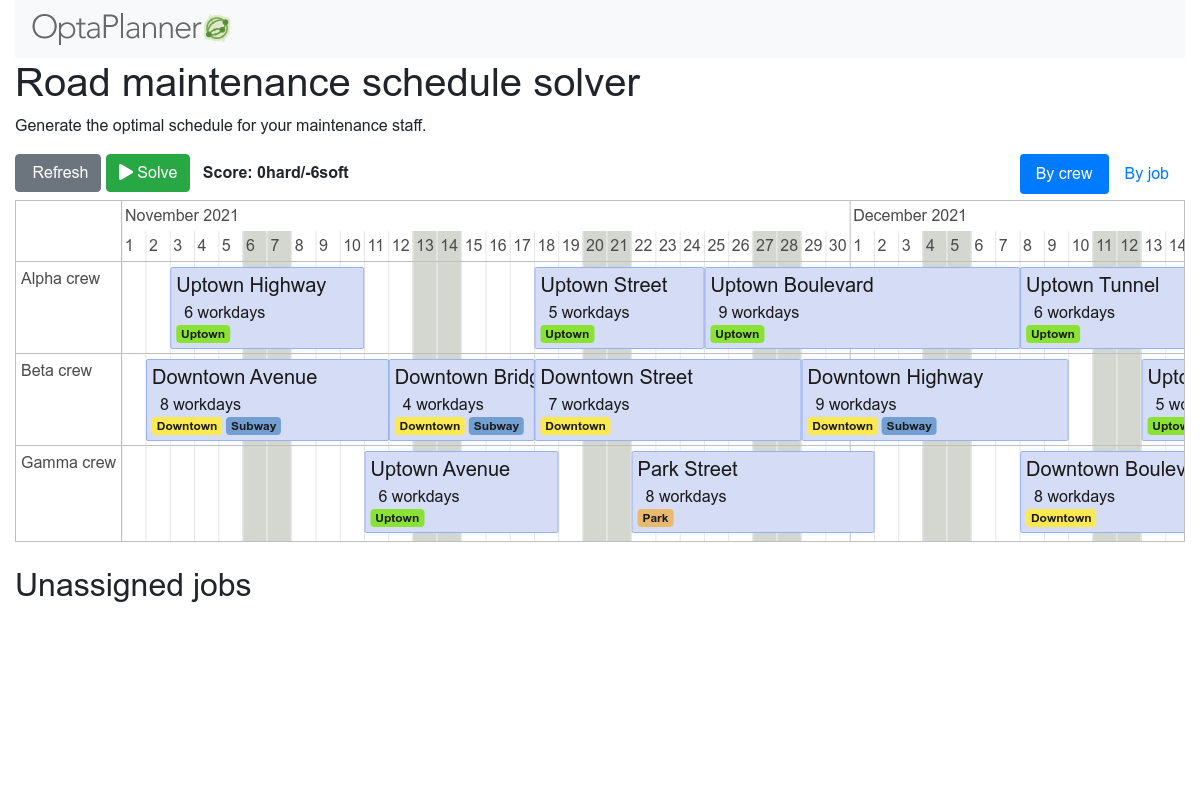
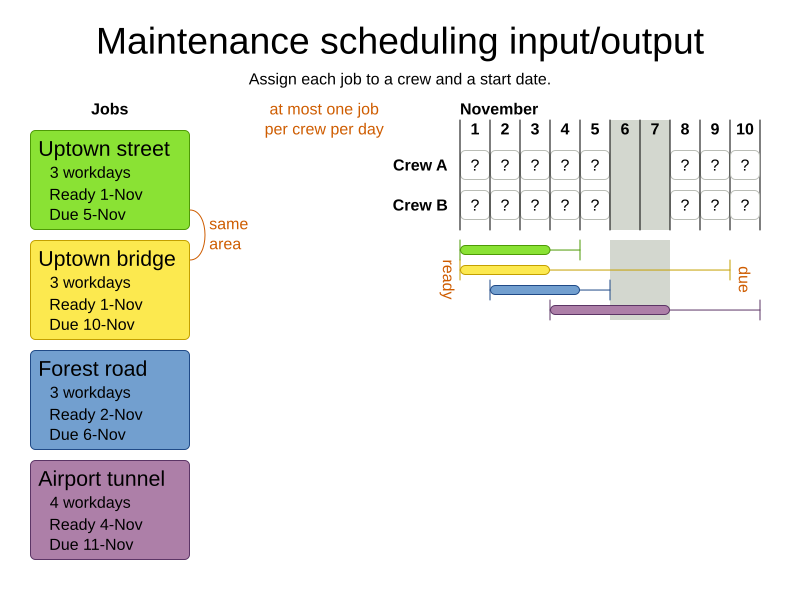
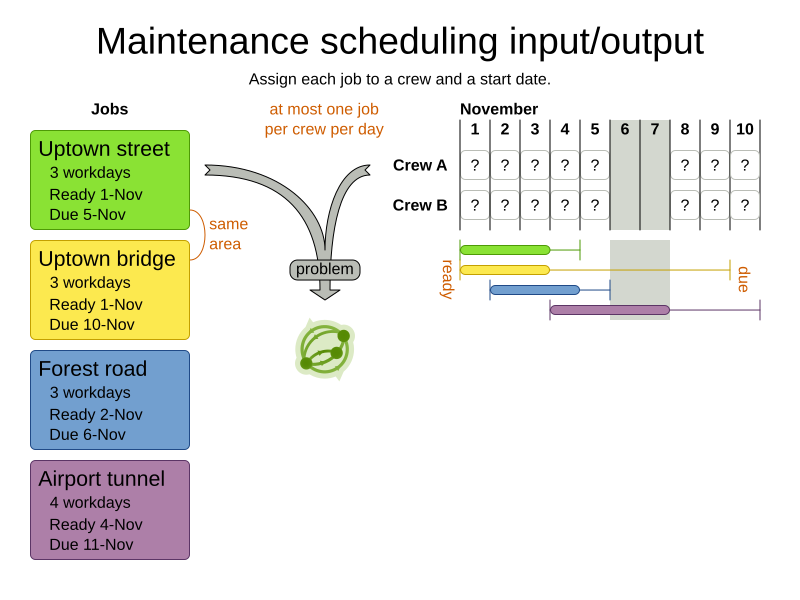
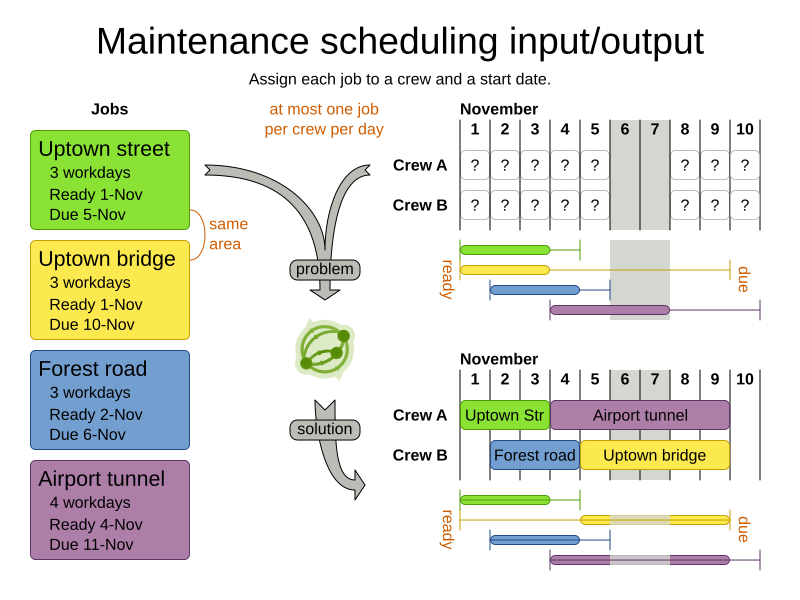






Domain


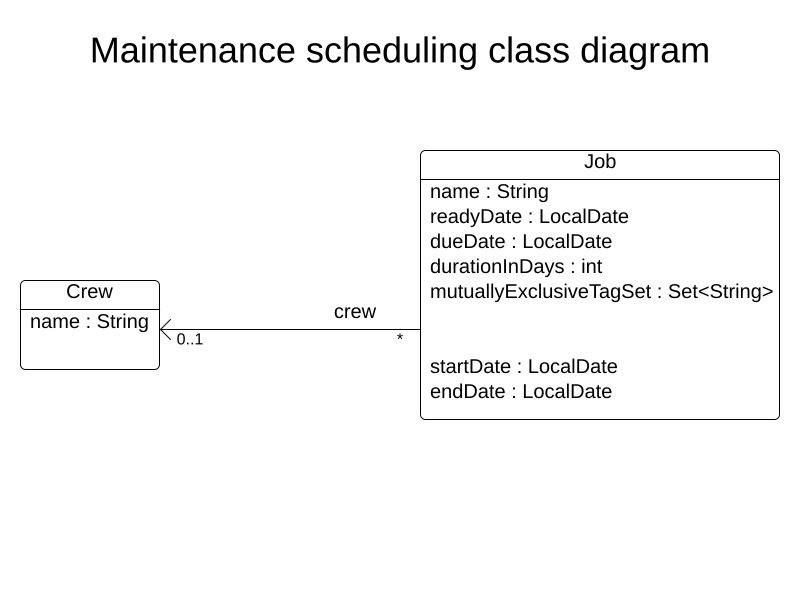
Project setup
https://code.quarkus.io


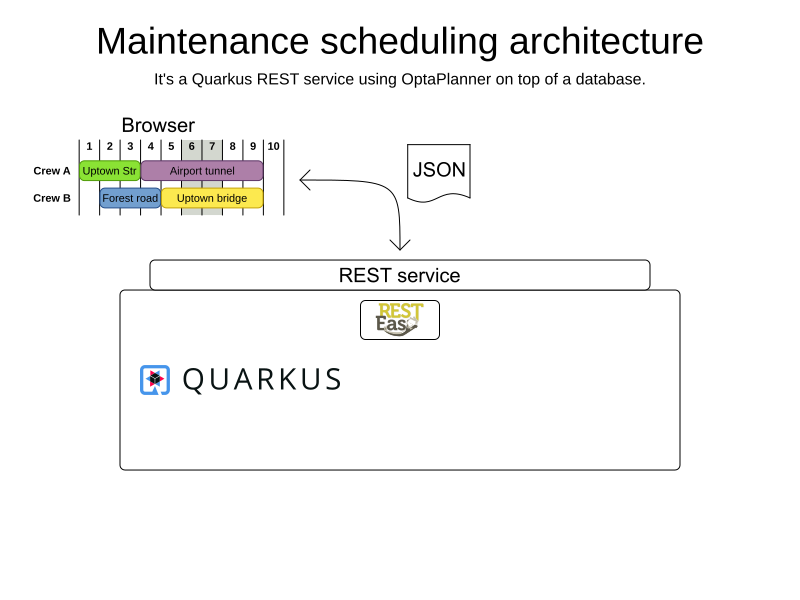
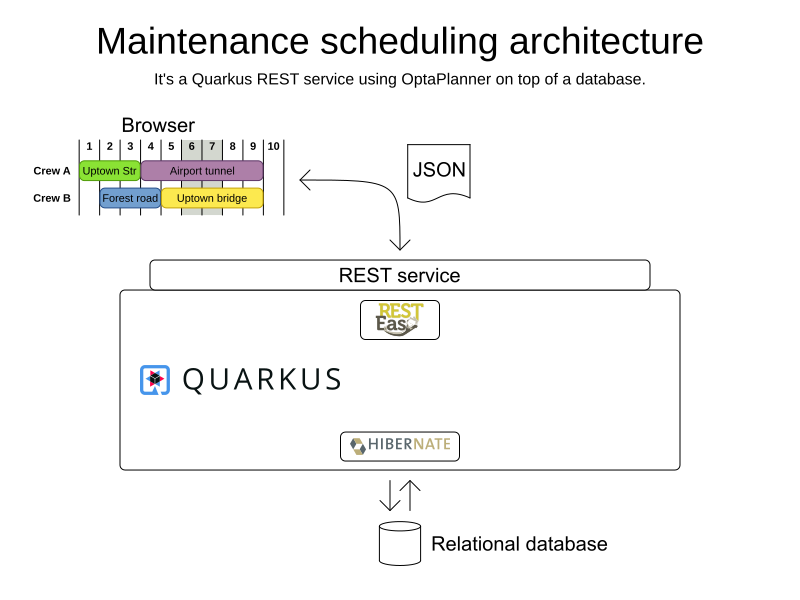
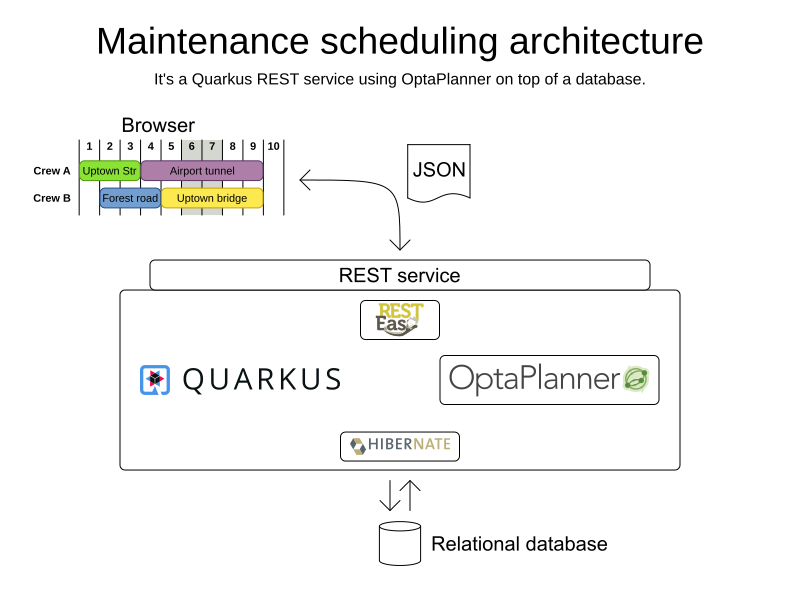
Coding
mvn quarkus:dev
AI planning optimization


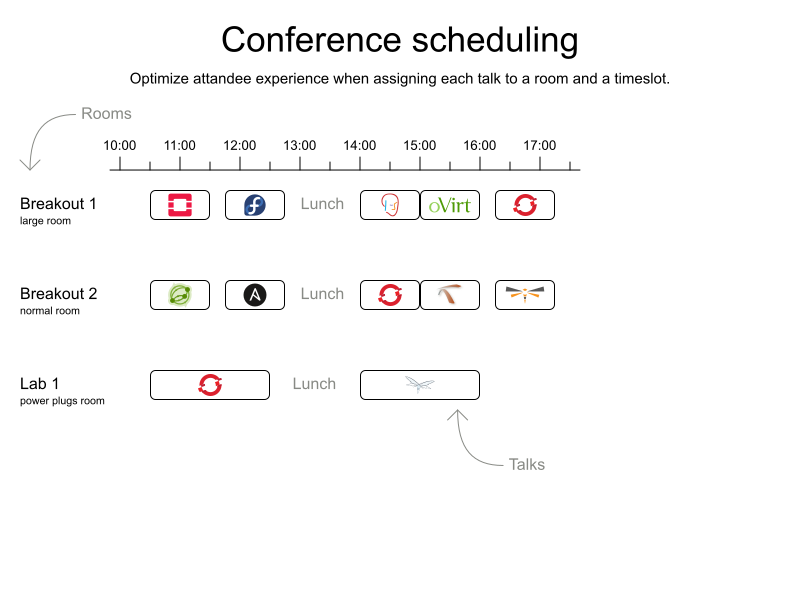
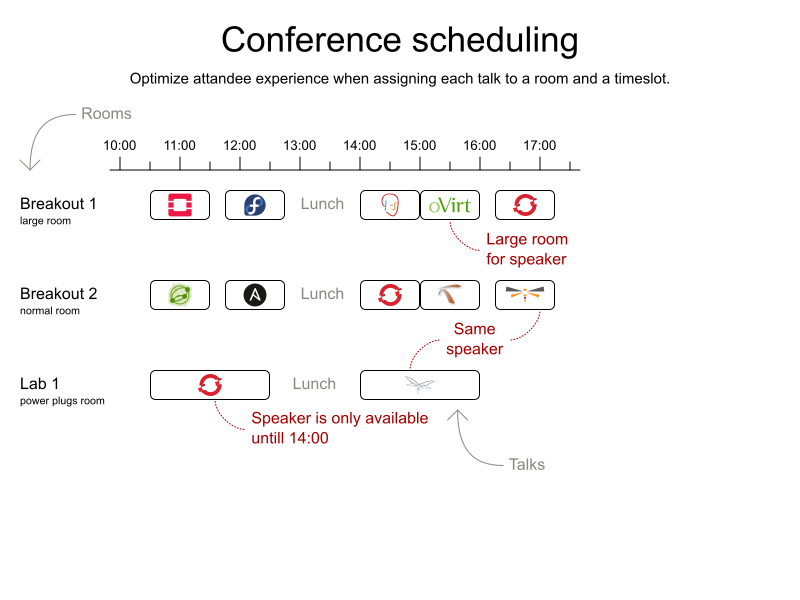
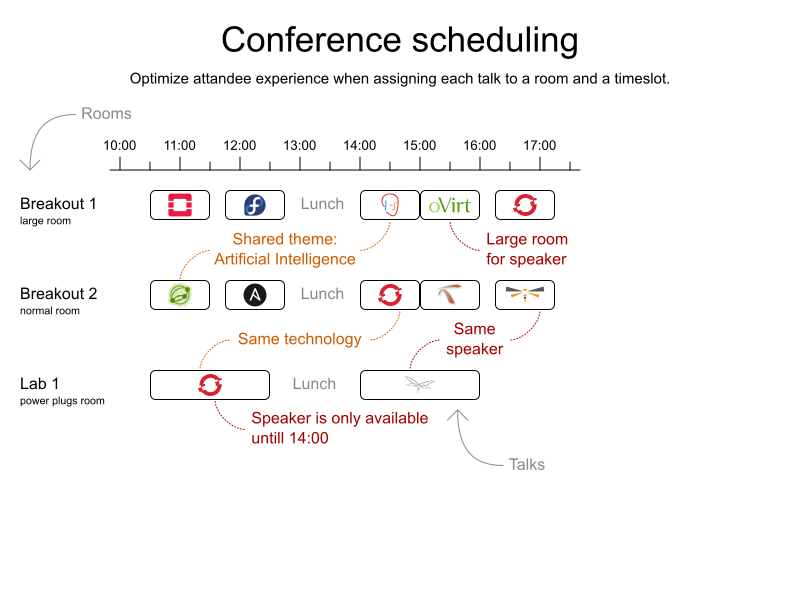
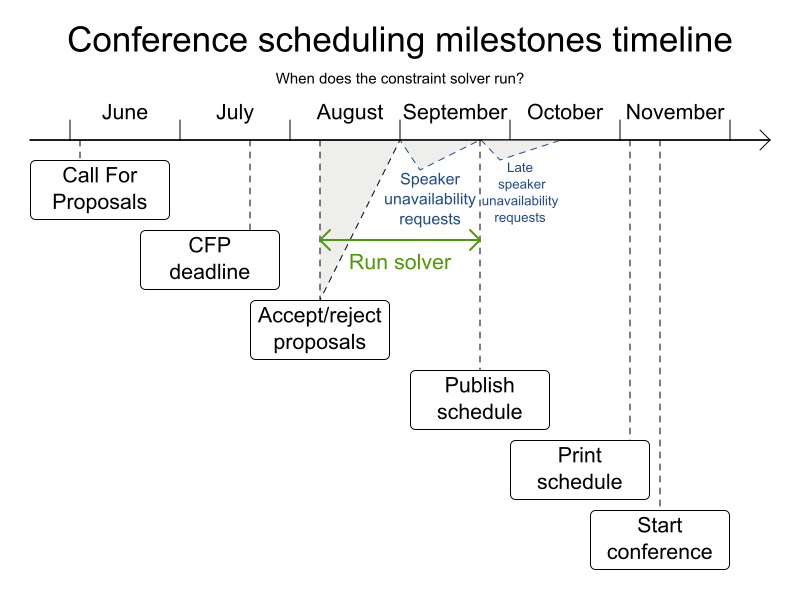
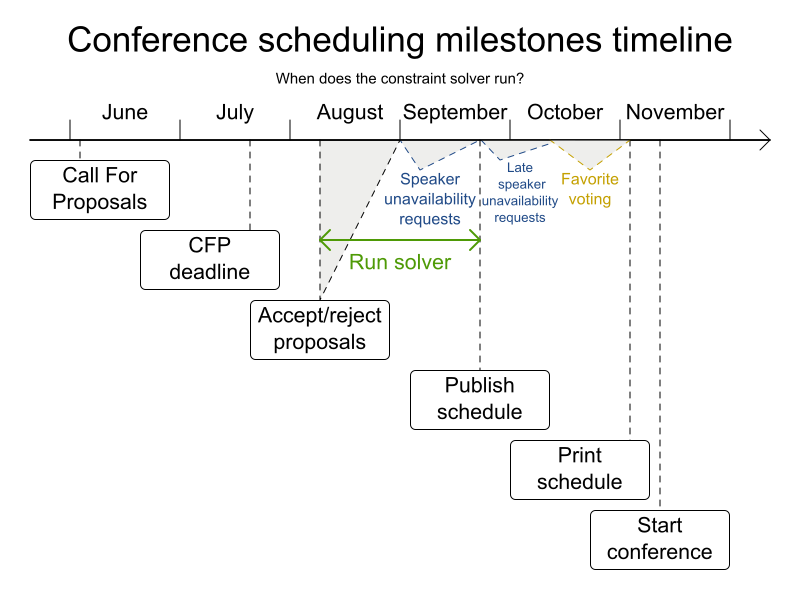
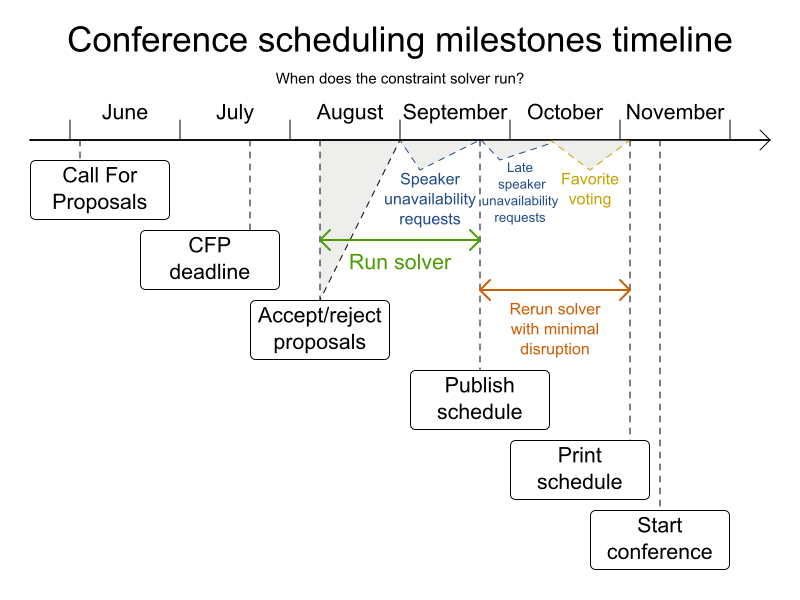
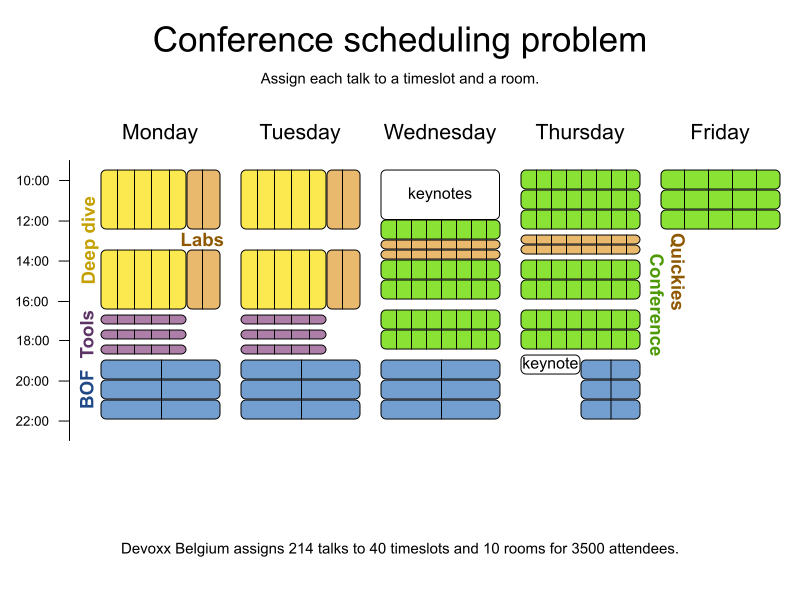
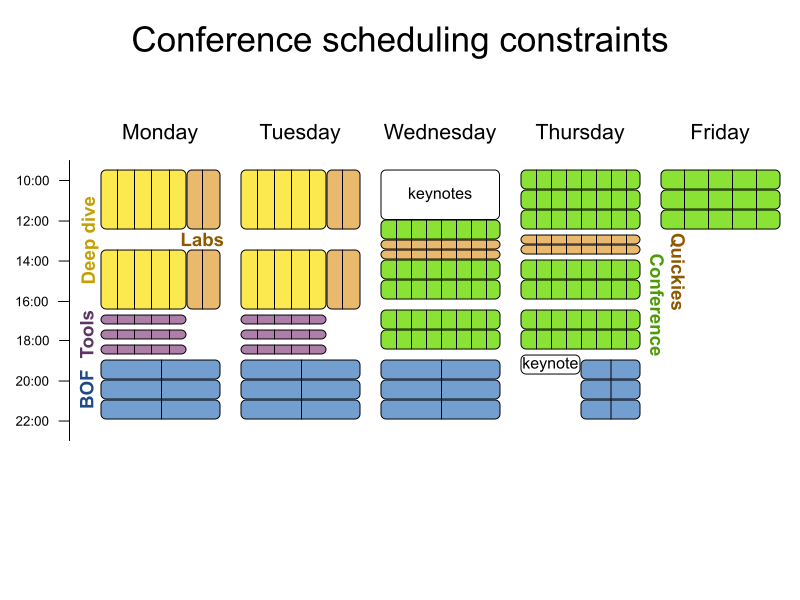
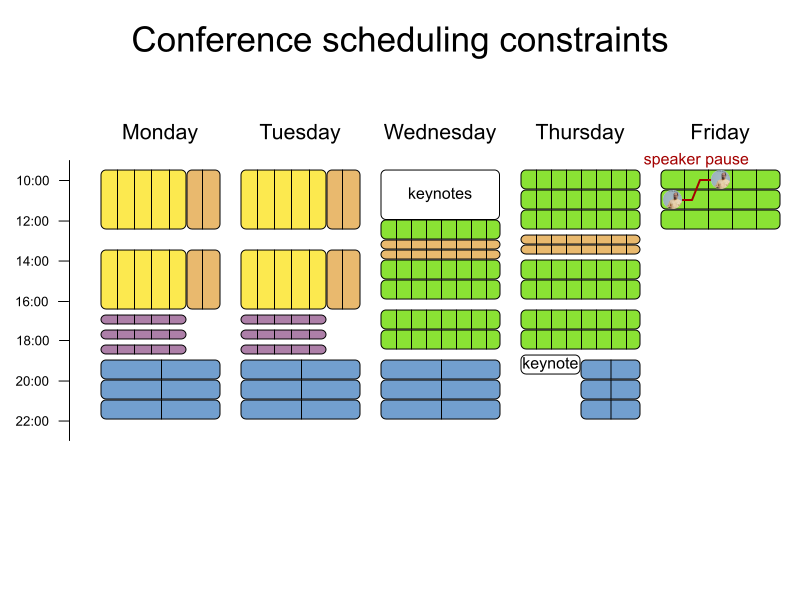
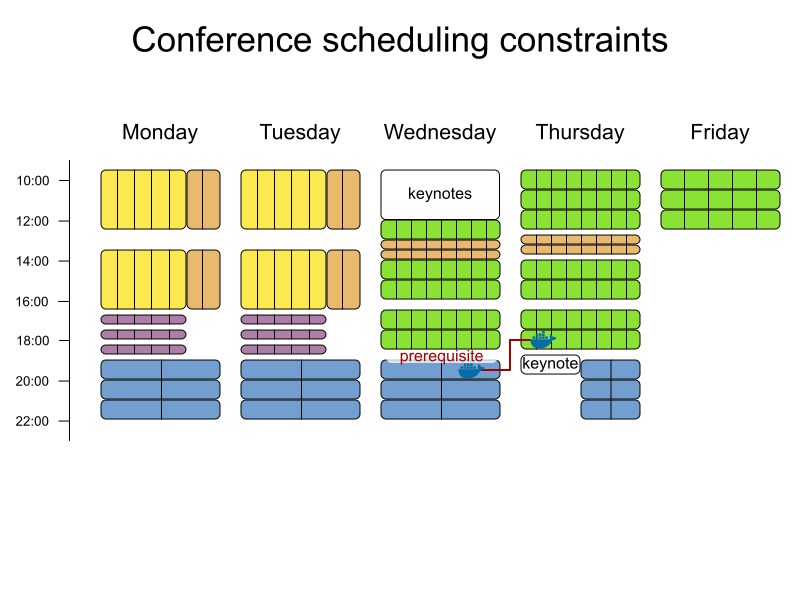
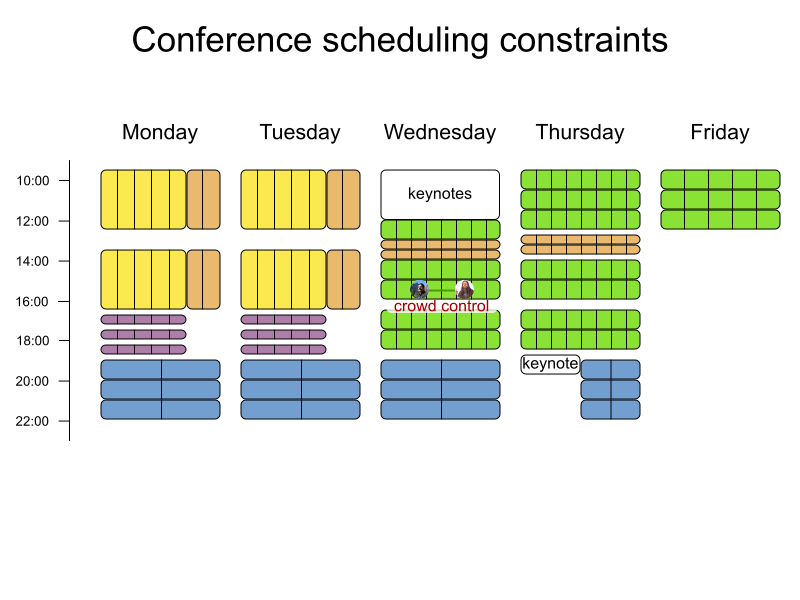
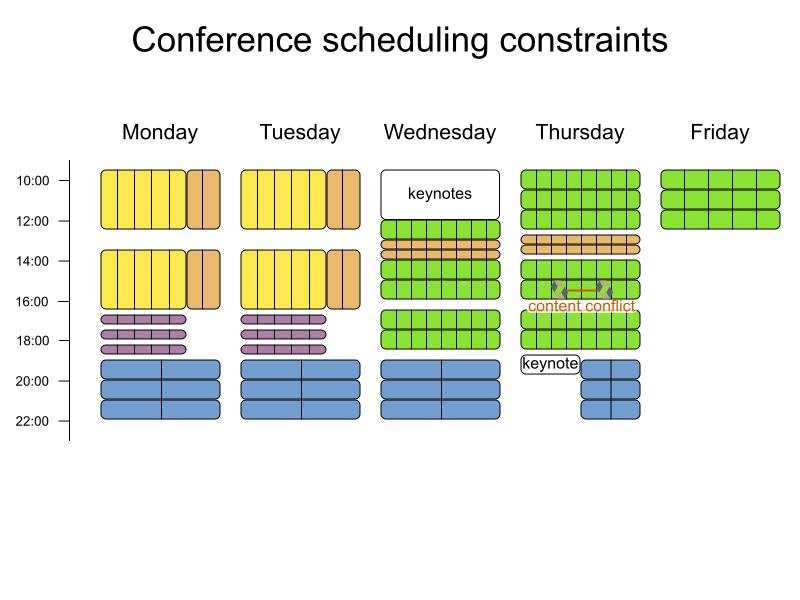
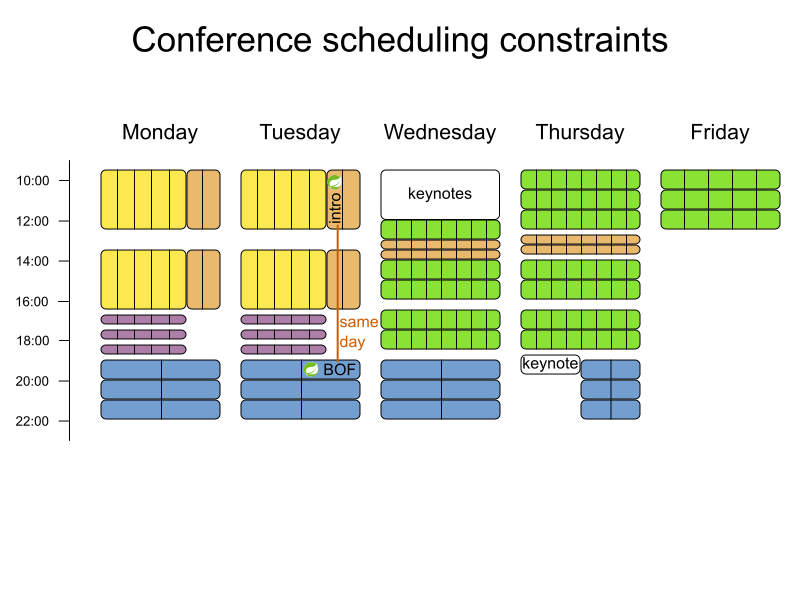
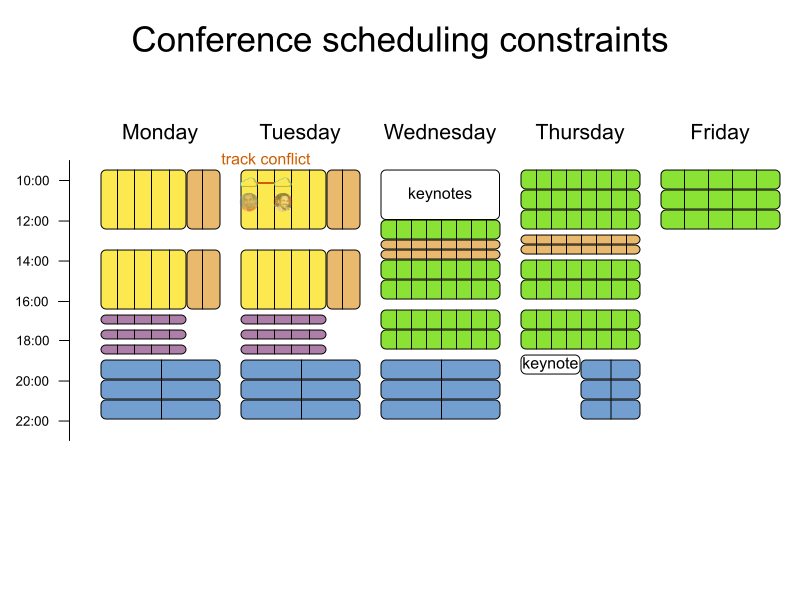
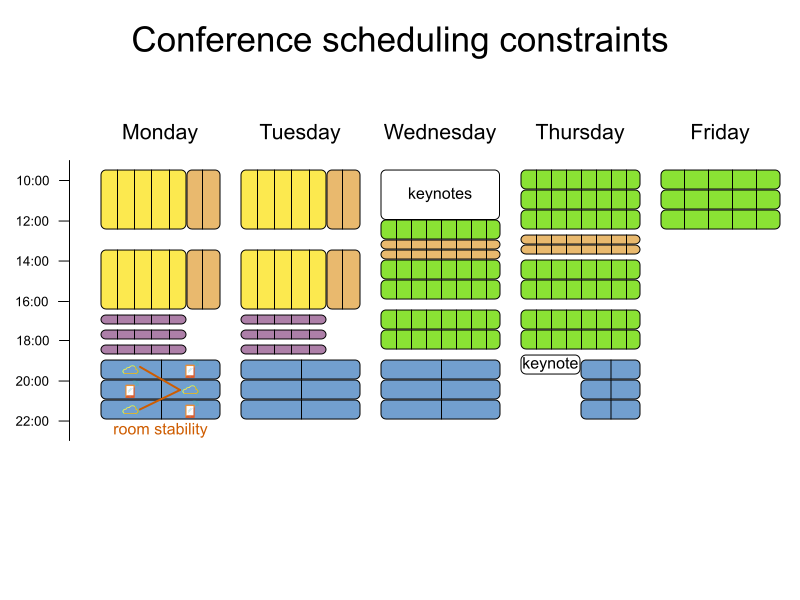
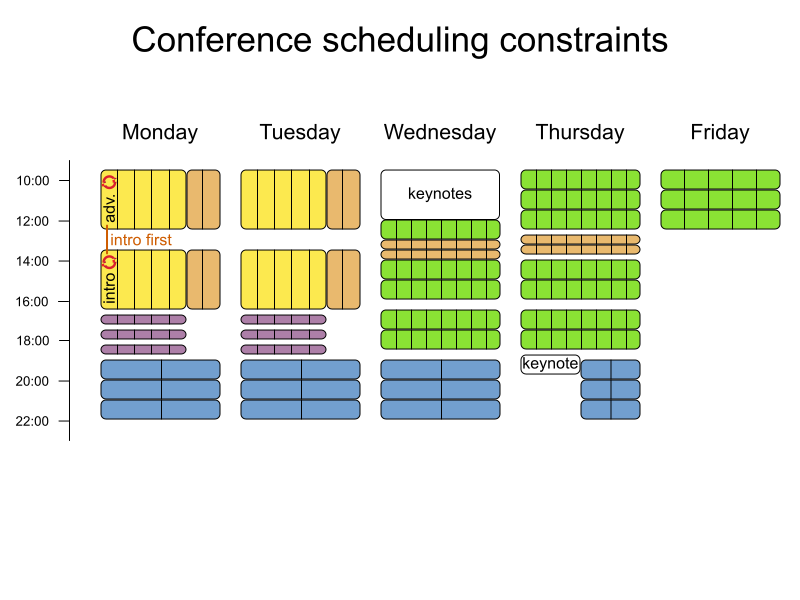
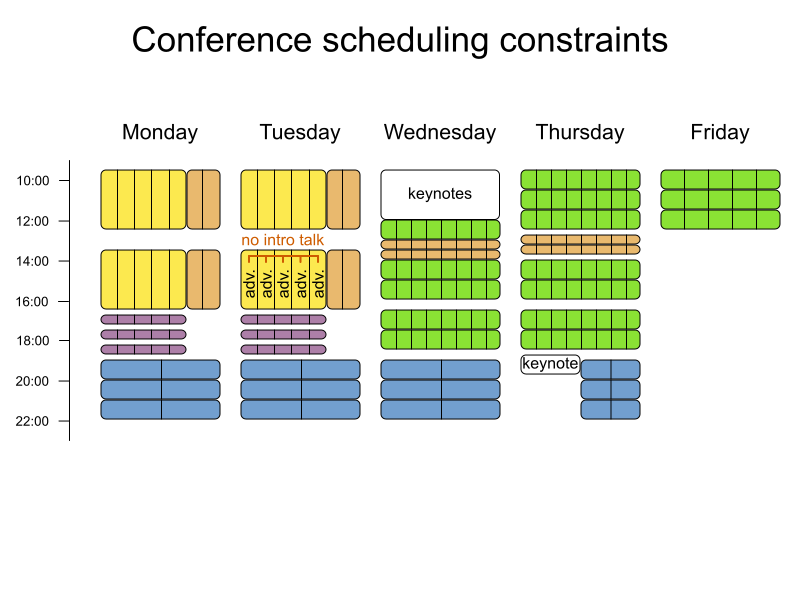
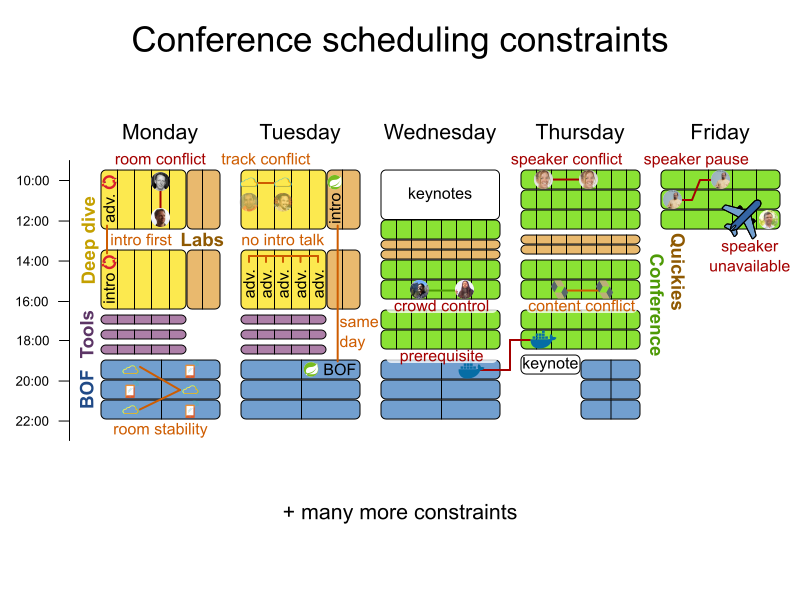
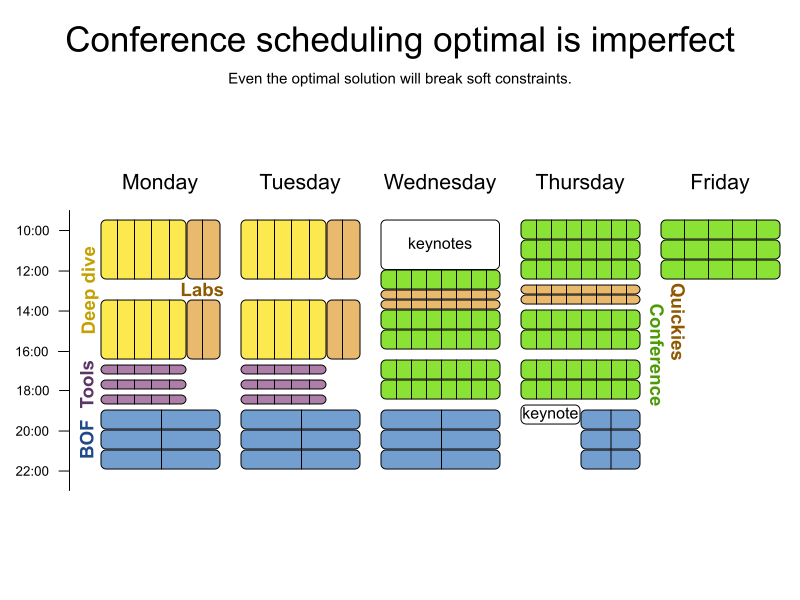
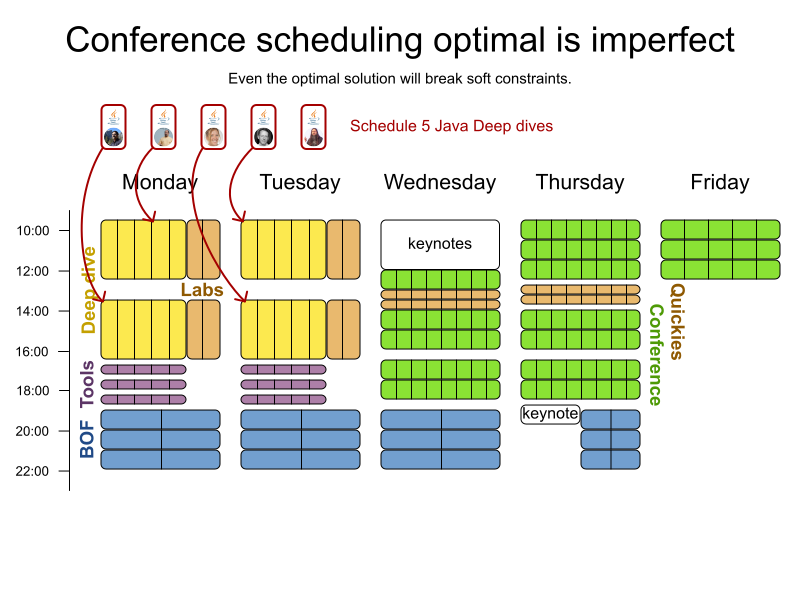
Conference scheduling
Press down to show
Press right to skip
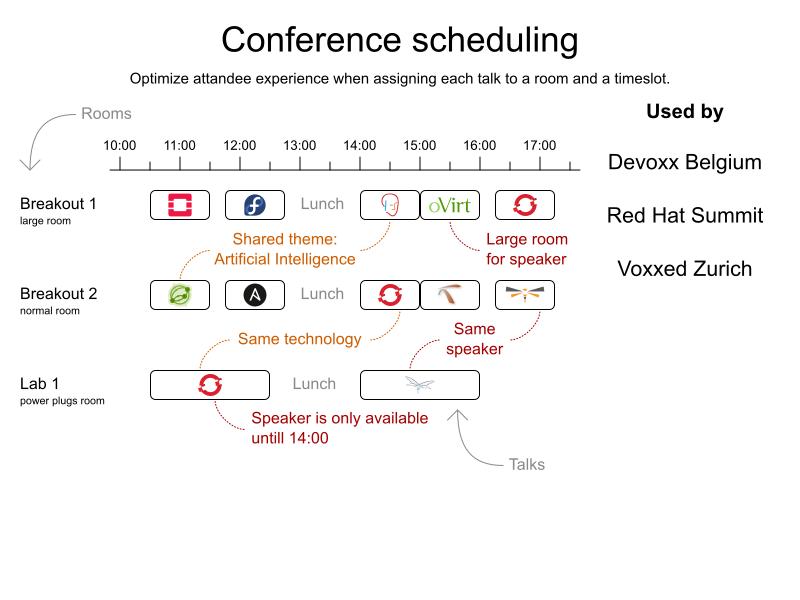
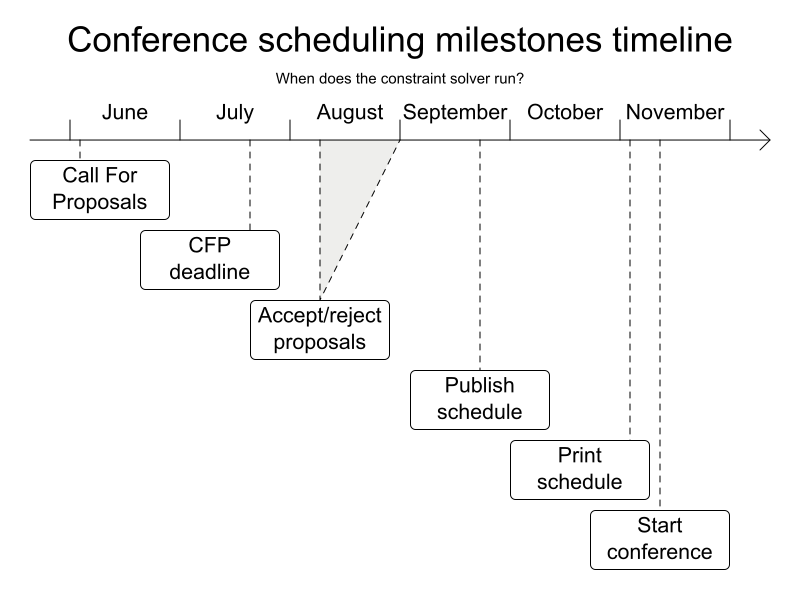
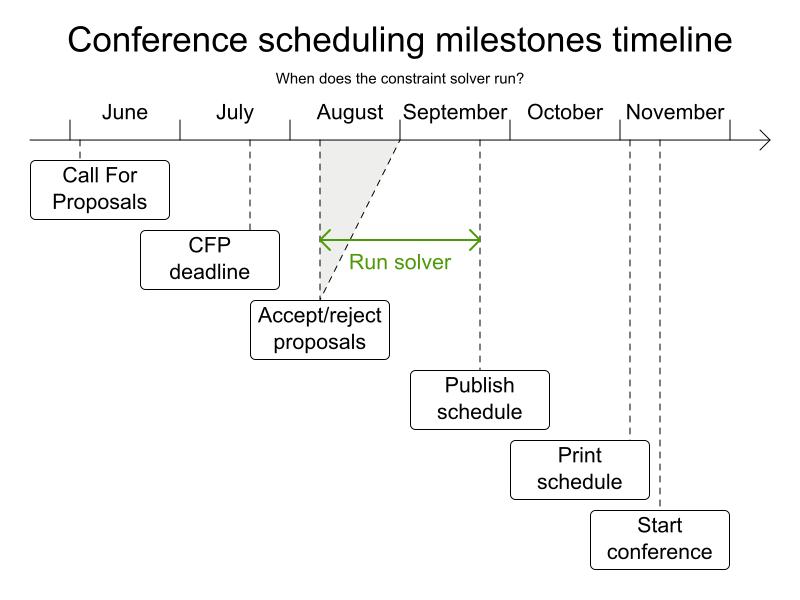
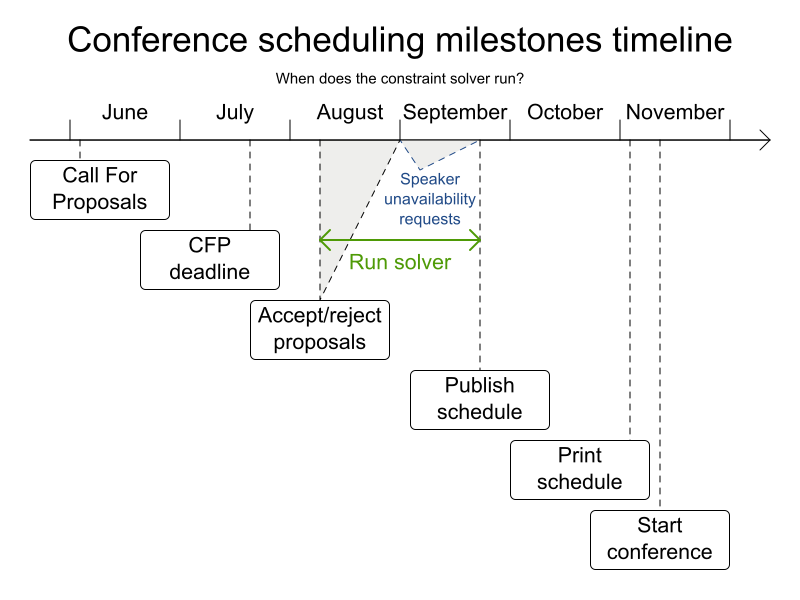
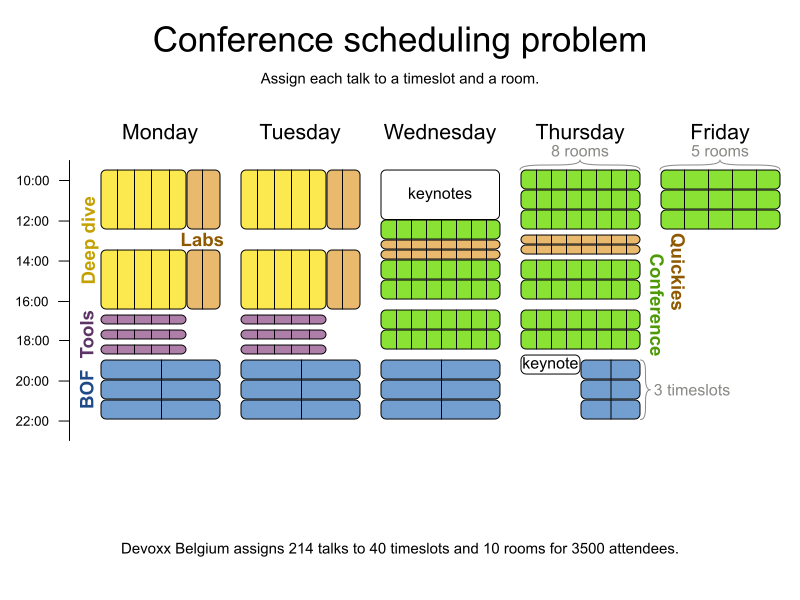
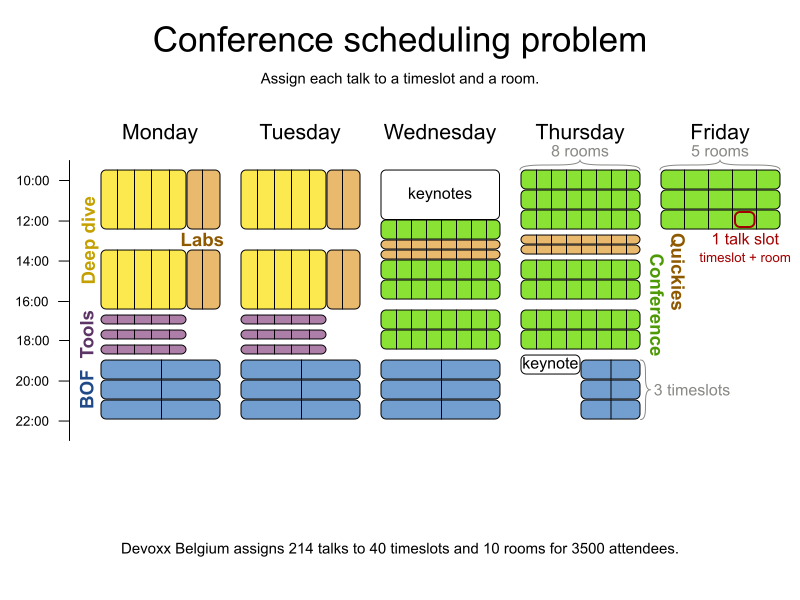
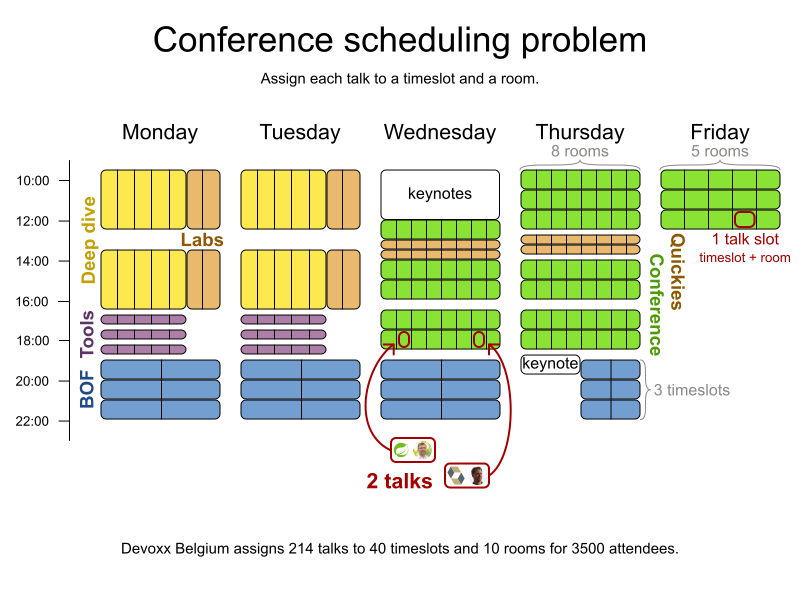
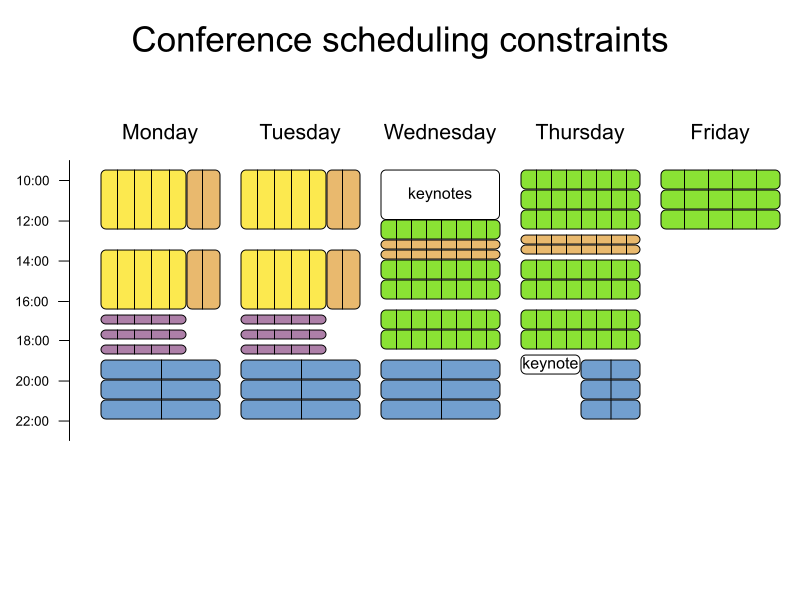
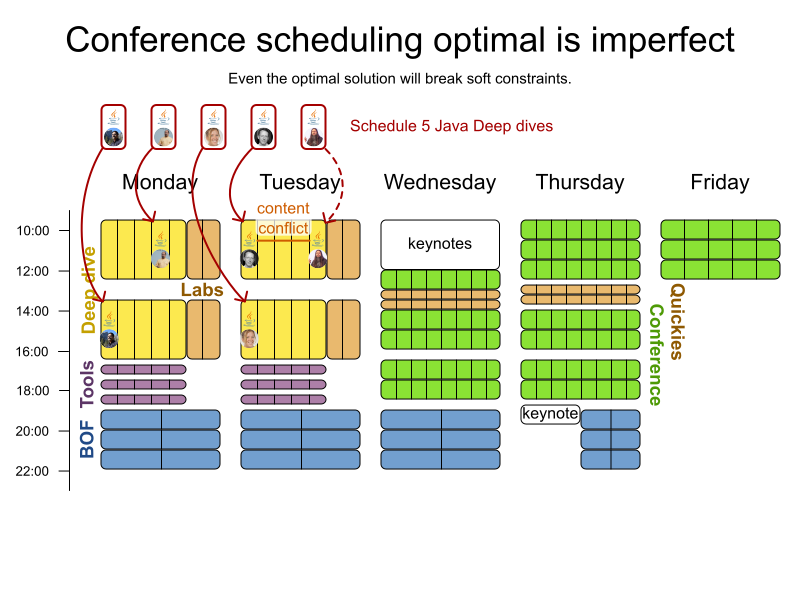
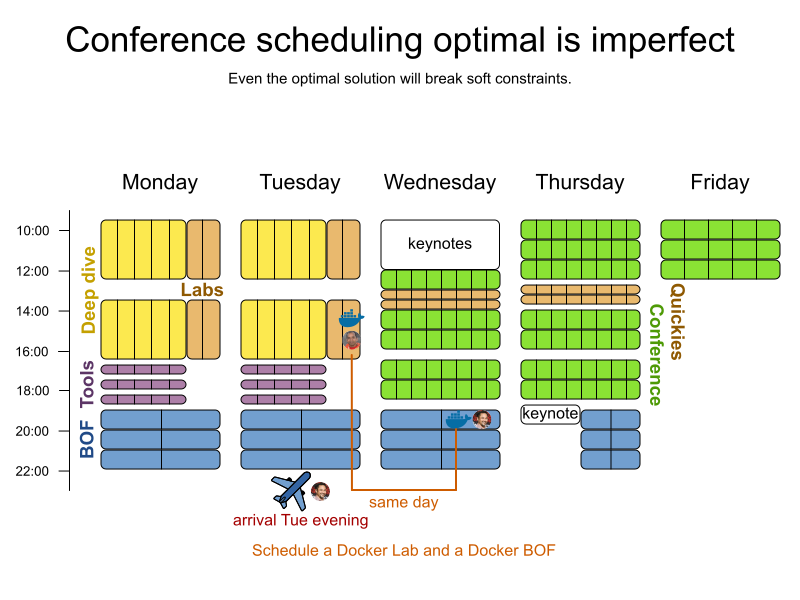
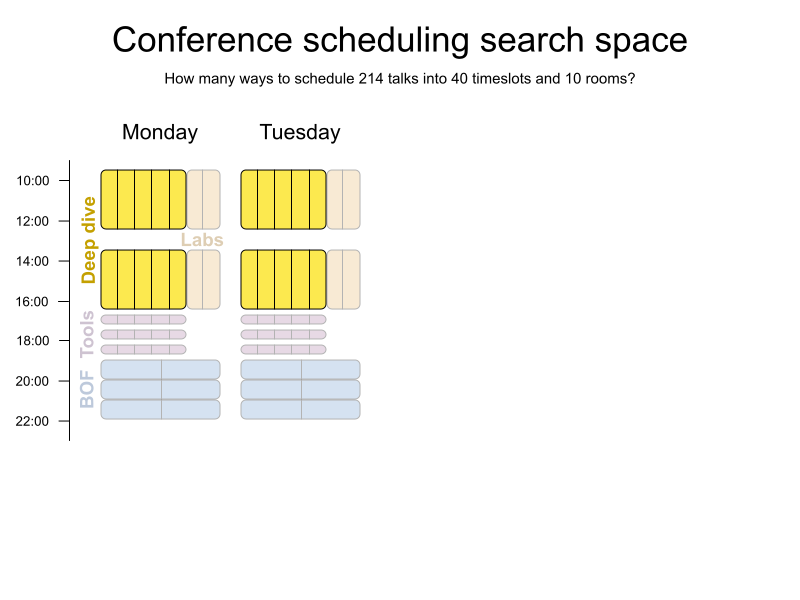
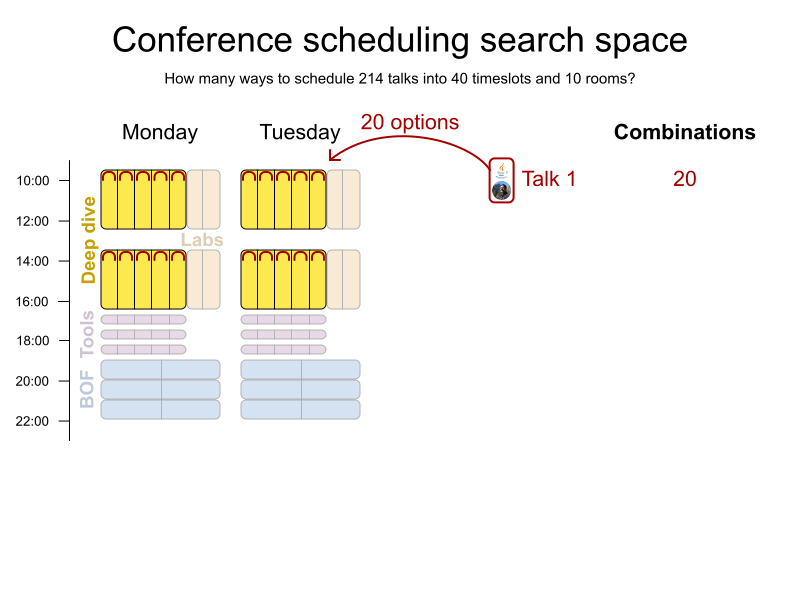
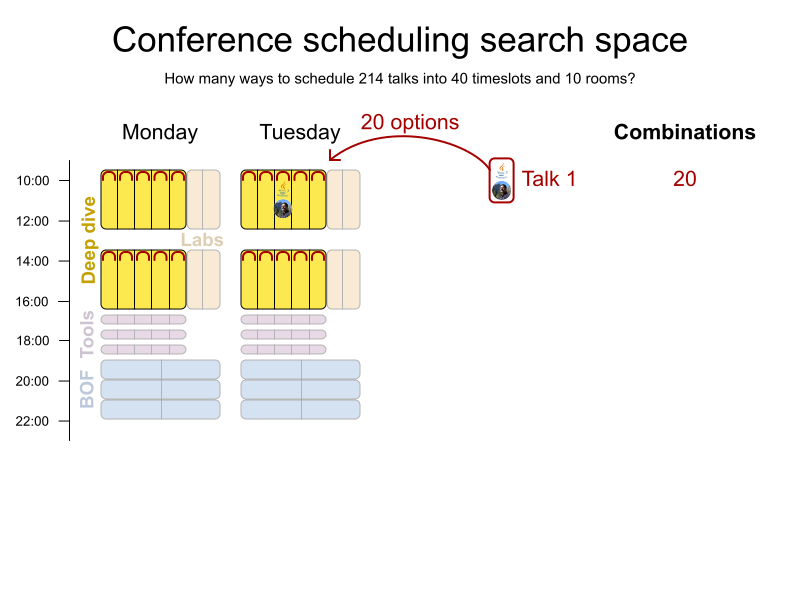
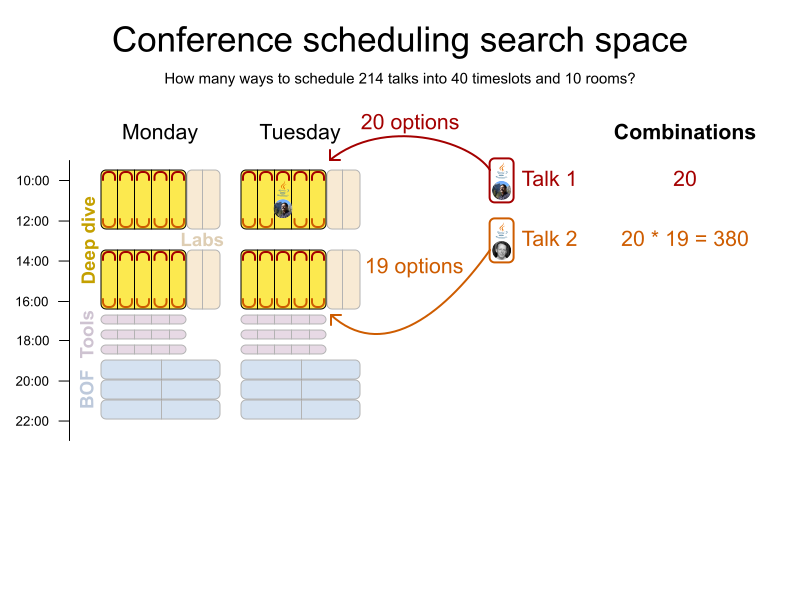
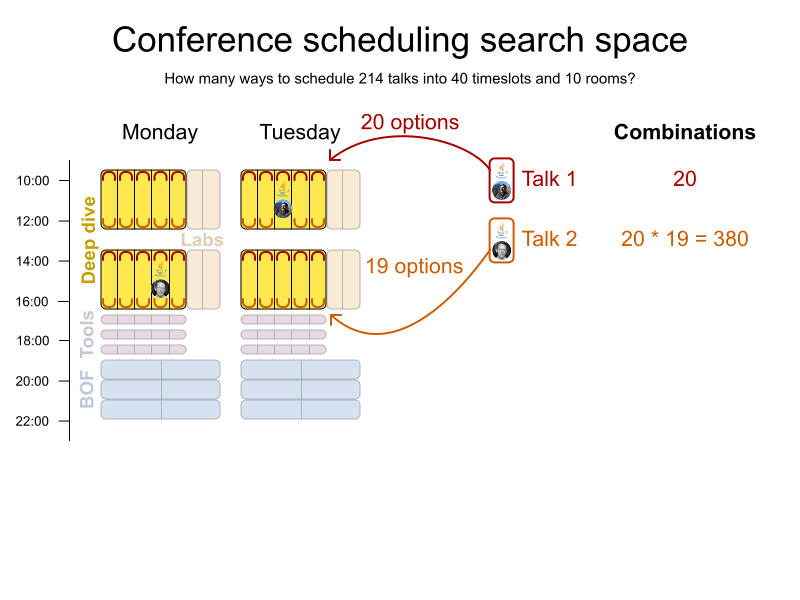
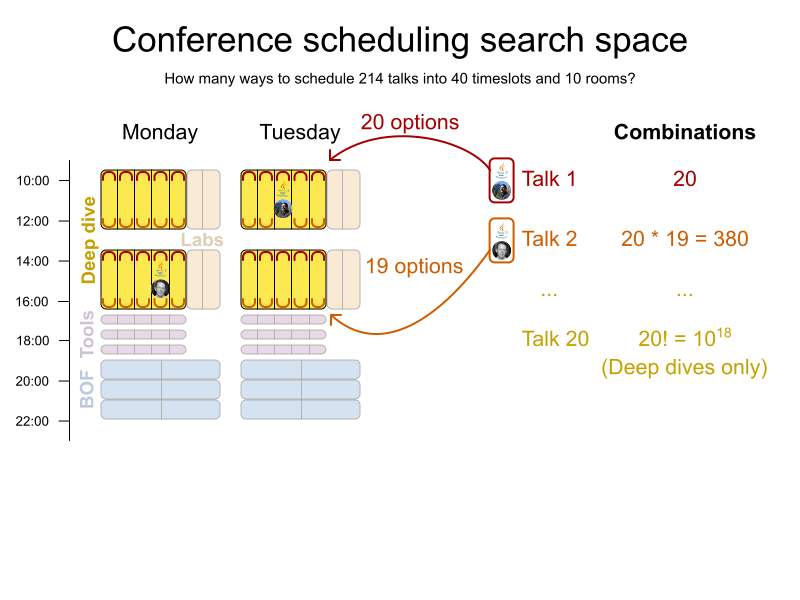
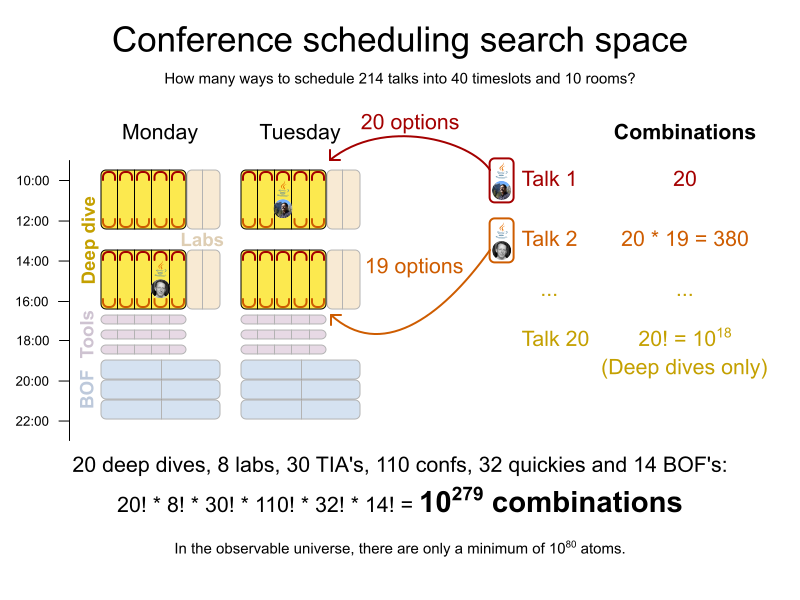
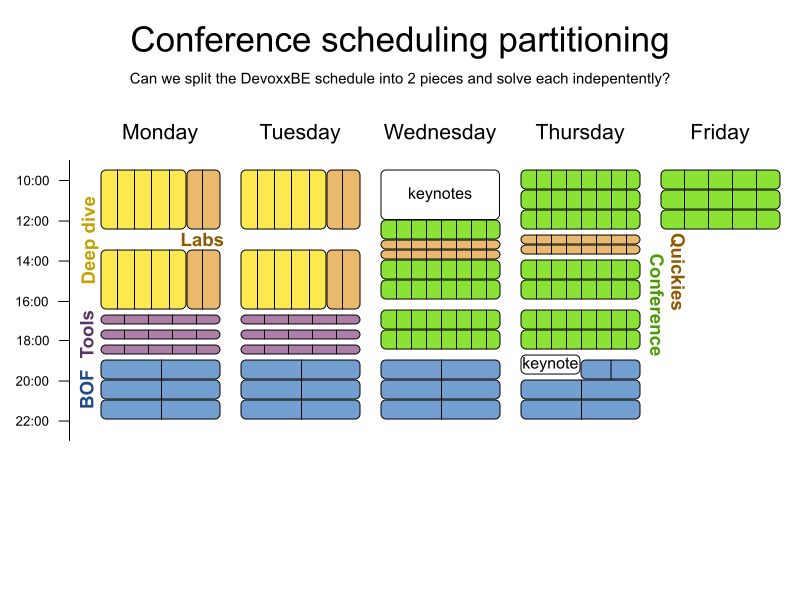
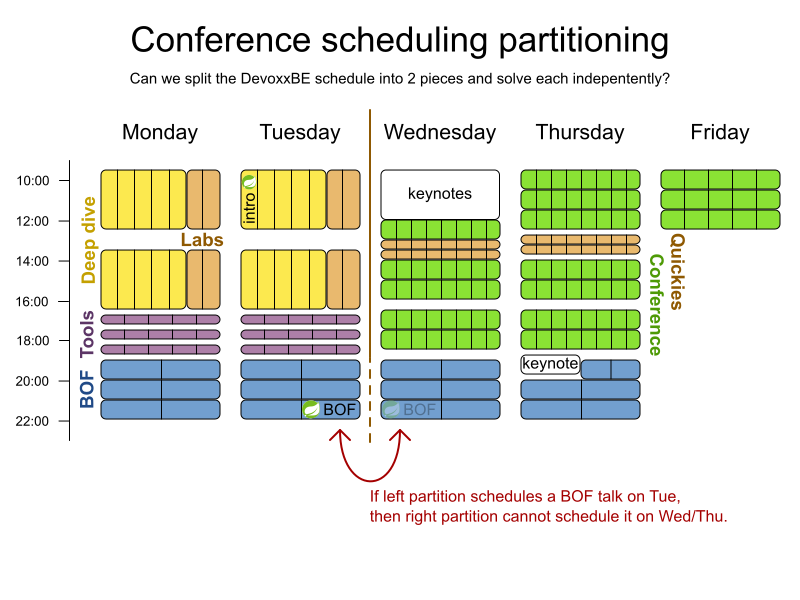
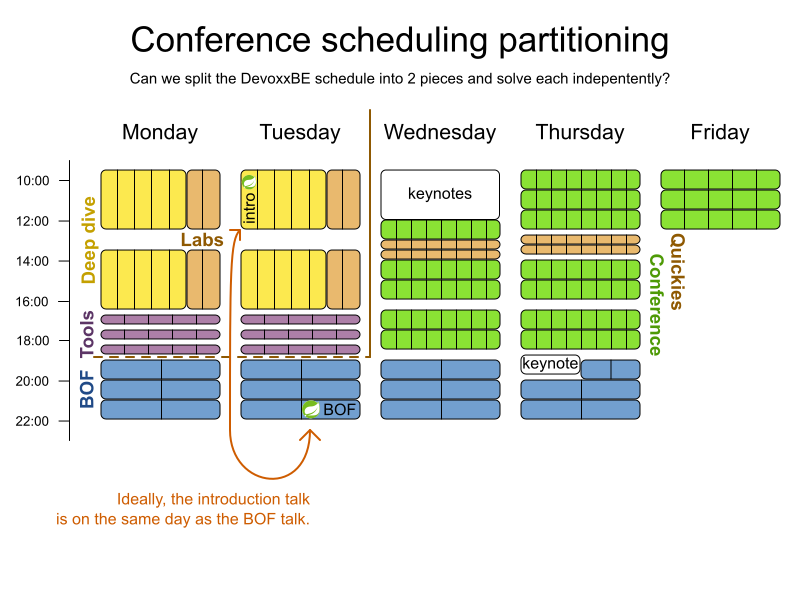
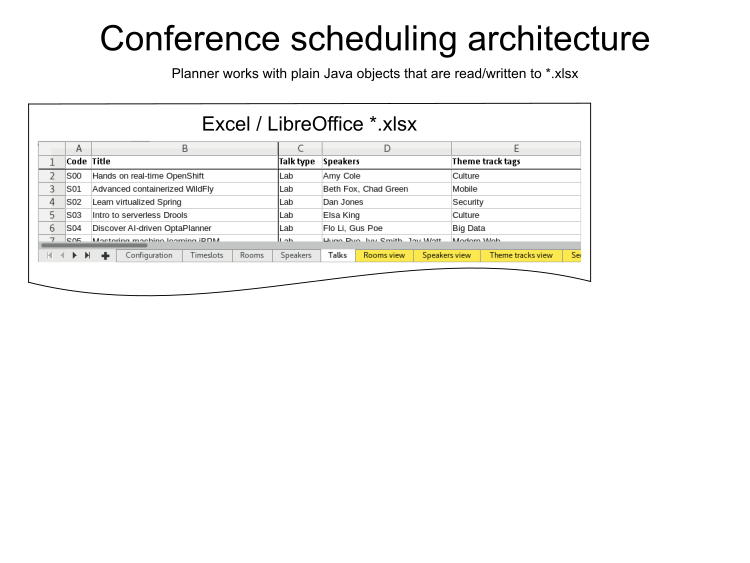
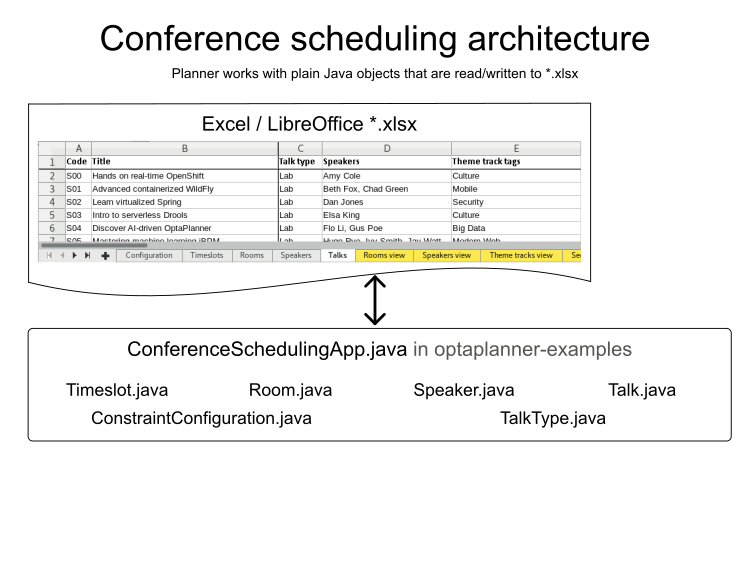
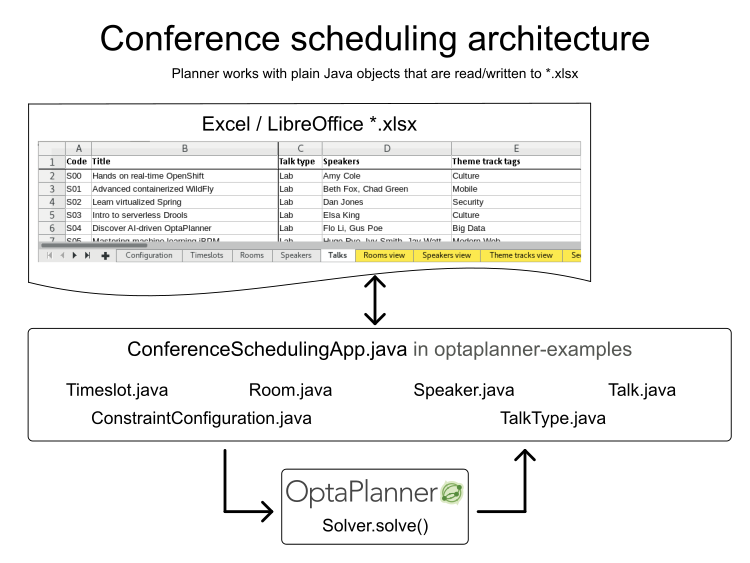
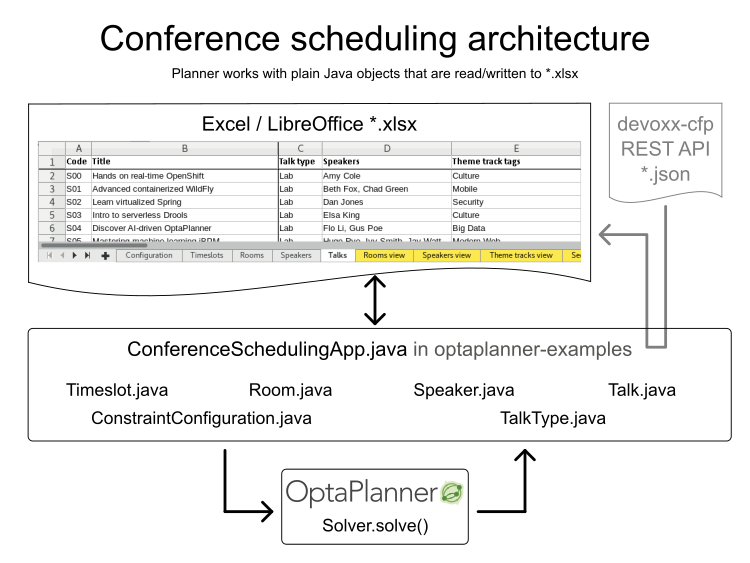
Implementation
- Define domain
- Define constraints
- Solve
Define domain
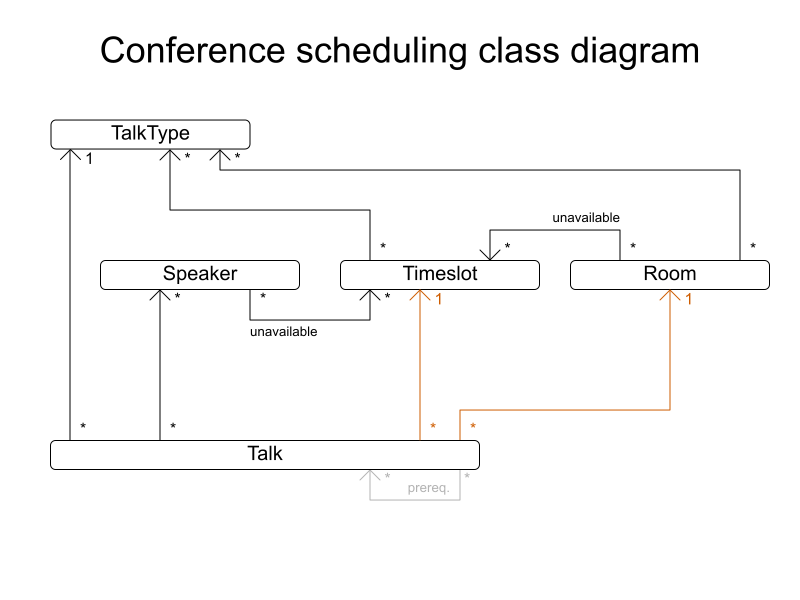
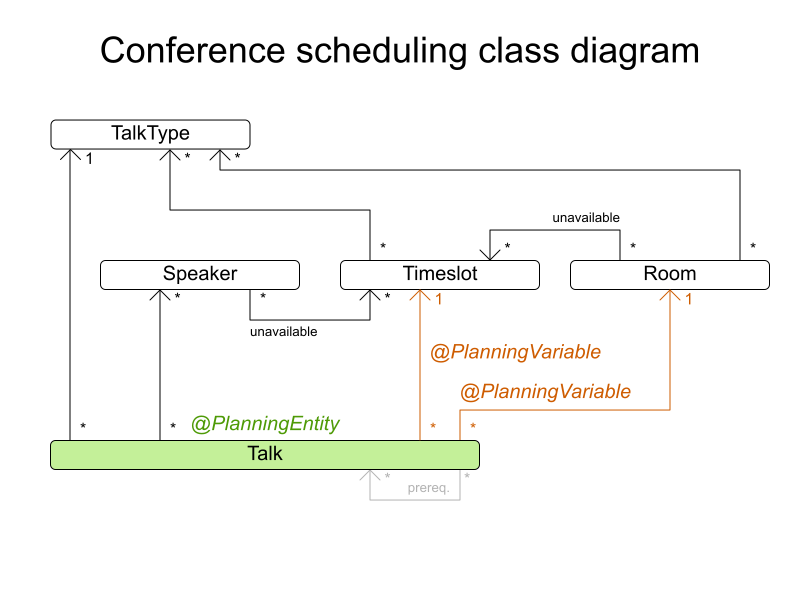
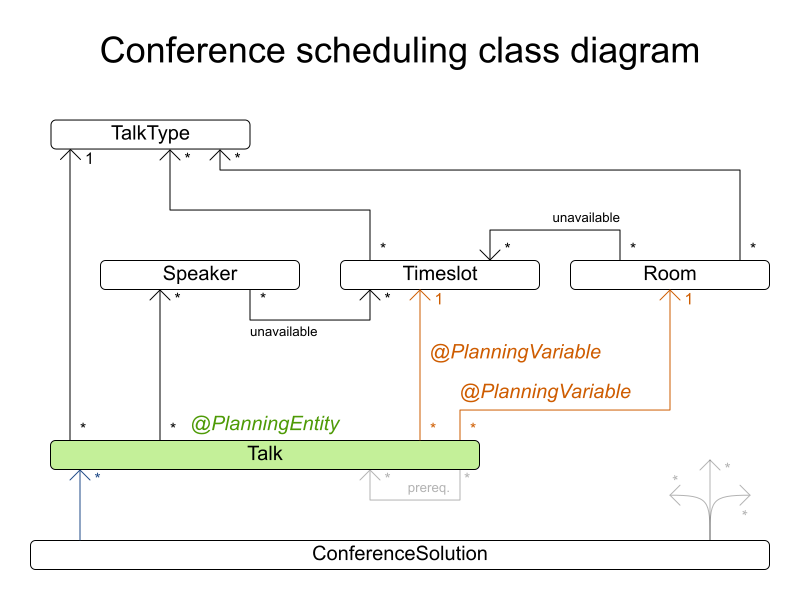
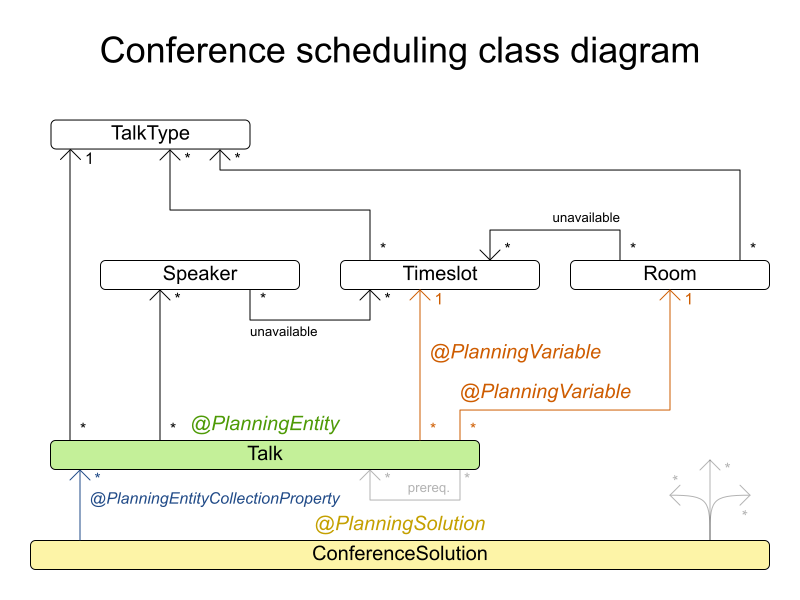
Timeslot.java
public class Timeslot {
private LocalDateTime startDateTime;
private LocalDateTime endDateTime;
...
} Plain old java class
Room.java
public class Room {
private String name;
private int capacity;
...
} Plain old java class
Speaker.java
public class Speaker {
private String name;
...
} Plain old java class
Talk.java
public class Talk {
private String code;
private String title;
private TalkType talkType;
private List<Speaker> speakerList;
...
@PlanningVariable(valueRangeProviderRefs = "timeslotRange")
private Timeslot timeslot;
@PlanningVariable(valueRangeProviderRefs = "roomRange")
private Room room;
...
} Plain old java class with OptaPlanner annotations
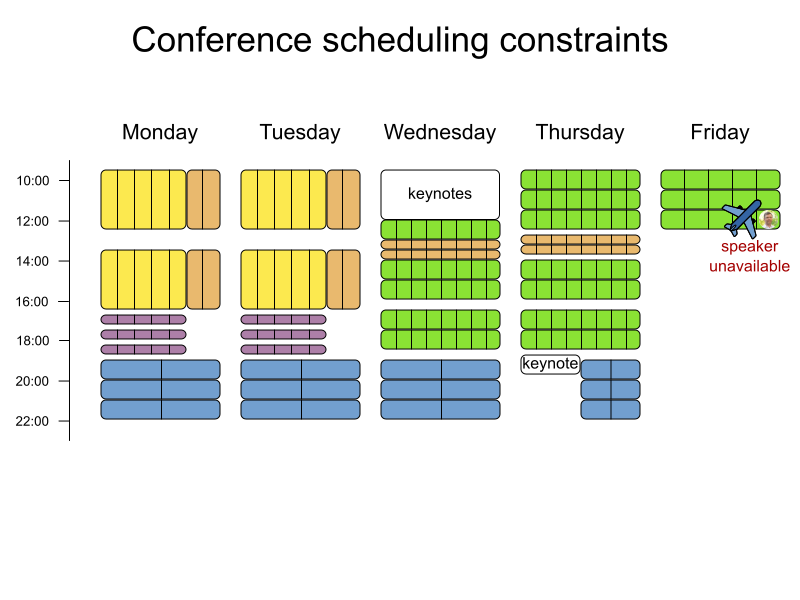
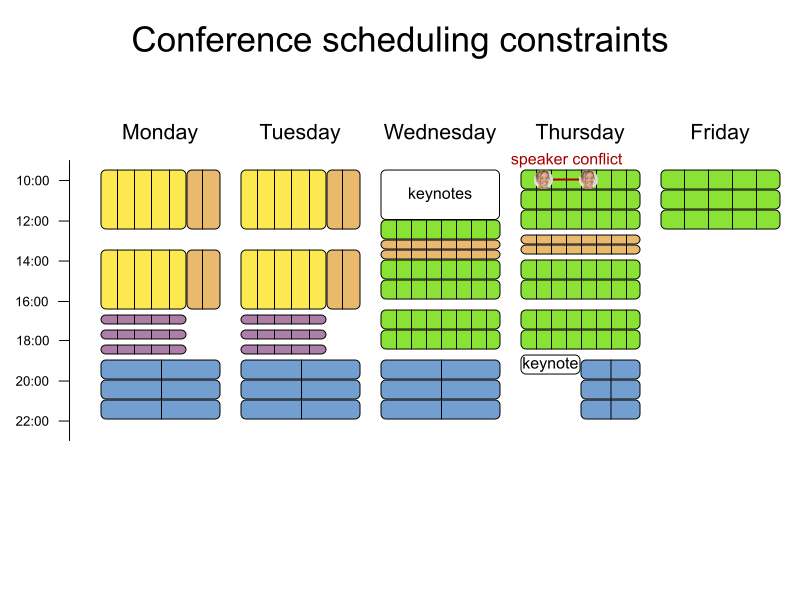
Define constraints
Score calculation
- Easy Java
- Incremental Java
- Drools DRL (also incremental)
Easy Java score calculation
- Easy to implement
- Bridge an existing system
- Slow
public class ConferenceSchedulingEasyScoreCalculator
implements EasyScoreCalculator<ConferenceSchedule> {
public HardMediumSoft calculateScore(ConferenceSchedule cs) {
int hardScore = 0;
for (Talk talk : cs.getTalkList()) {
if (talk.getTimeslot() != null
&& talk.hasUnavailableRoom()) {
hardScore--;
}
}
...
return HardMediumSoft.valueOf(
hardScore, mediumScore, softScore);
}
}Incremental Java score calculation
- Fast
- Solution changes ⇒ recalculate score delta only
- Hard to implement
- Much boilerplate code
Drools score calculation
- Incremental
- No boilerplate code
- Constraints in Drools Rule Language (DRL)
- Declarative (like SQL, regular expression)
rule "Room unavailable timeslot"
when
Talk(hasUnavailableRoom())
then
scoreHolder.penalize(kcontext);
endDemo
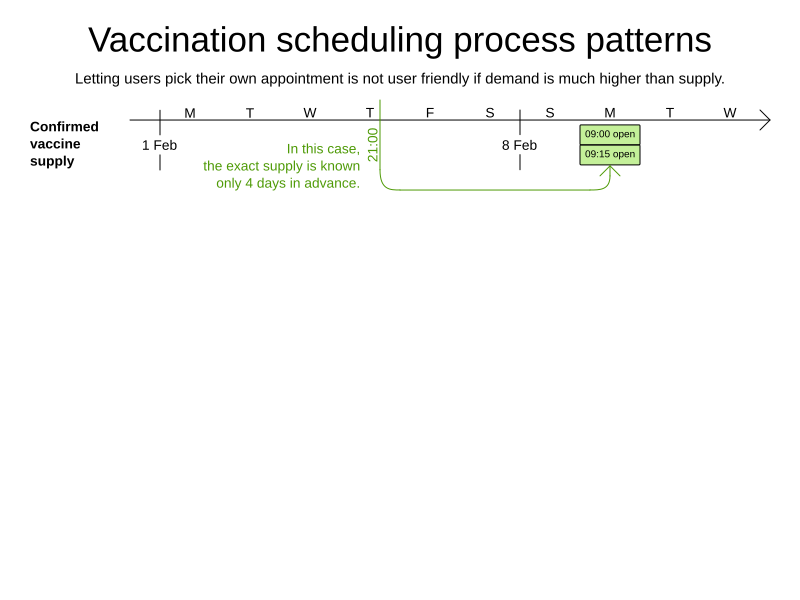
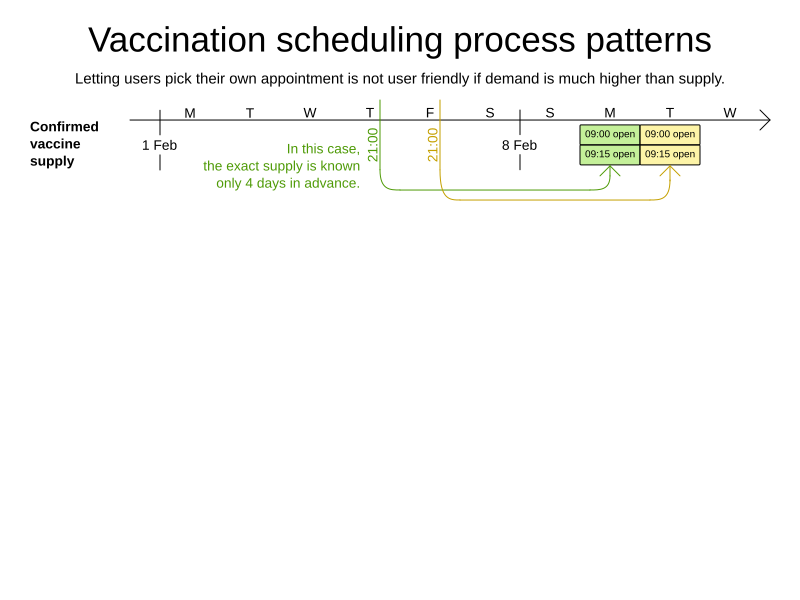
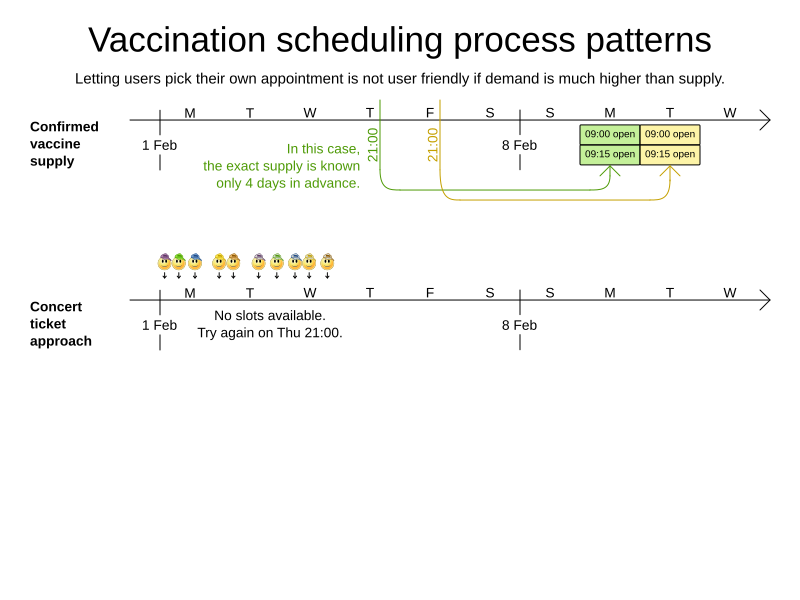
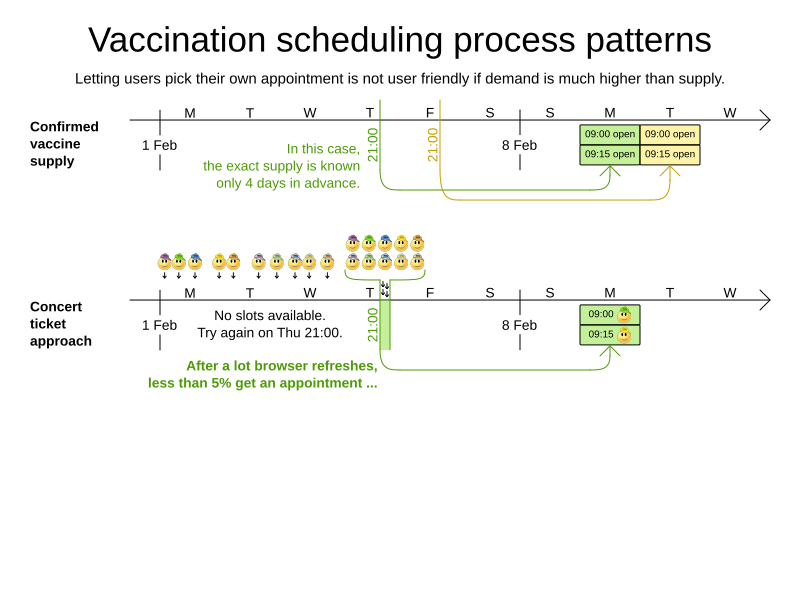
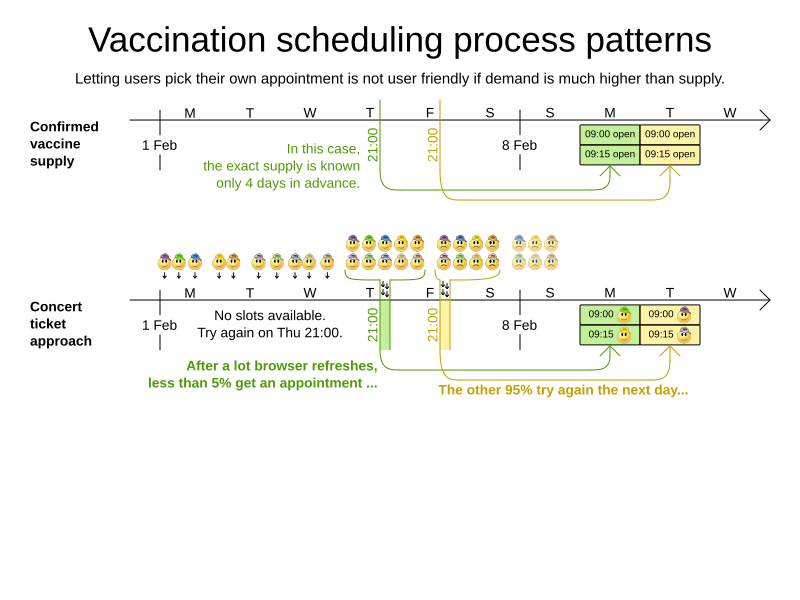
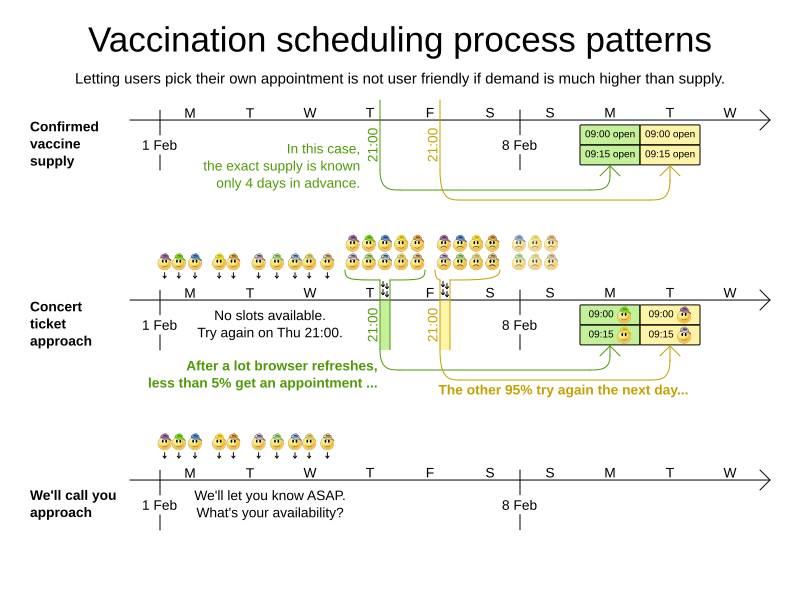
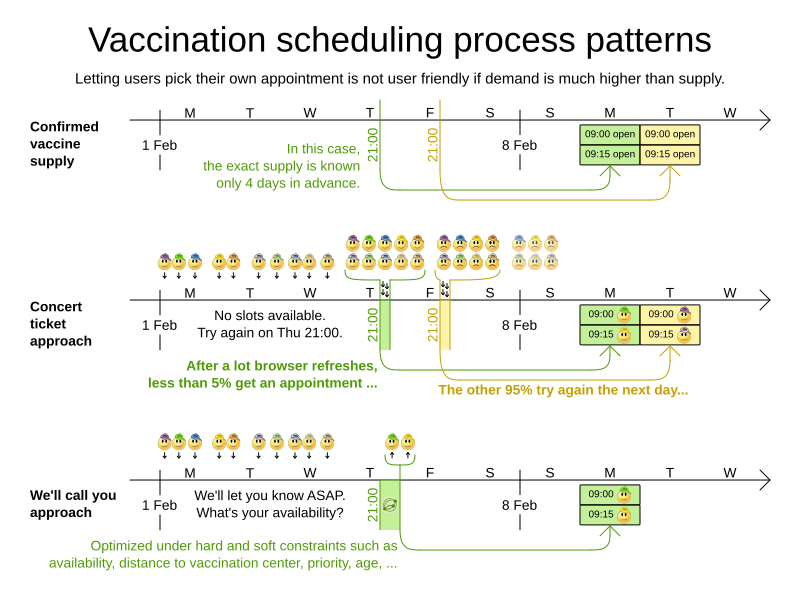
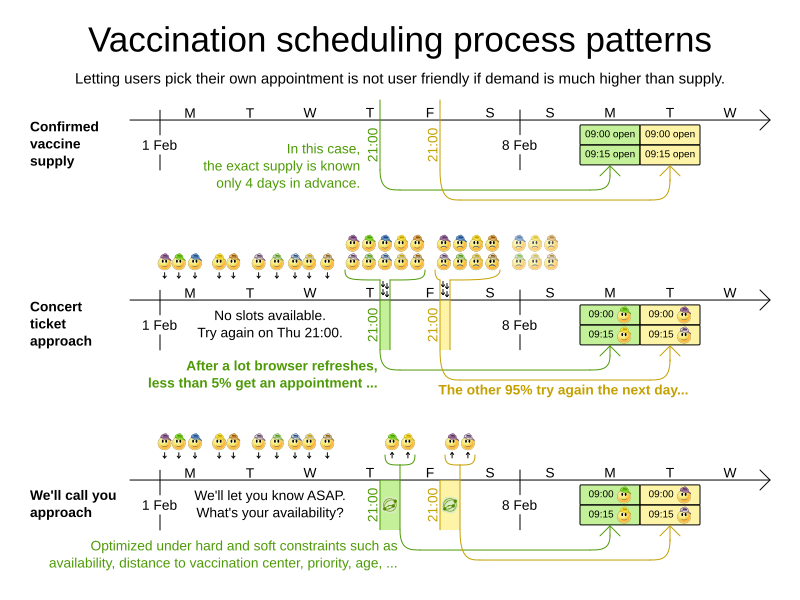
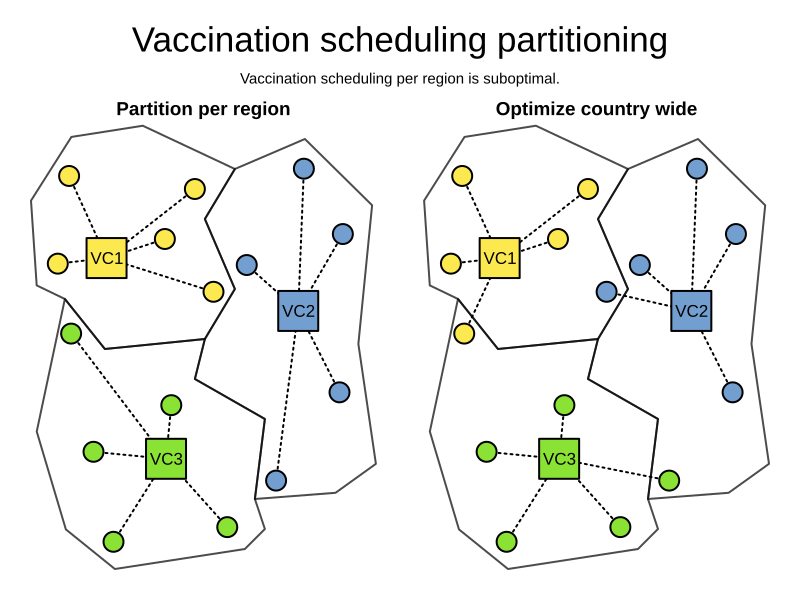
Vaccination appointment scheduling
Press down to show
Press right to skip
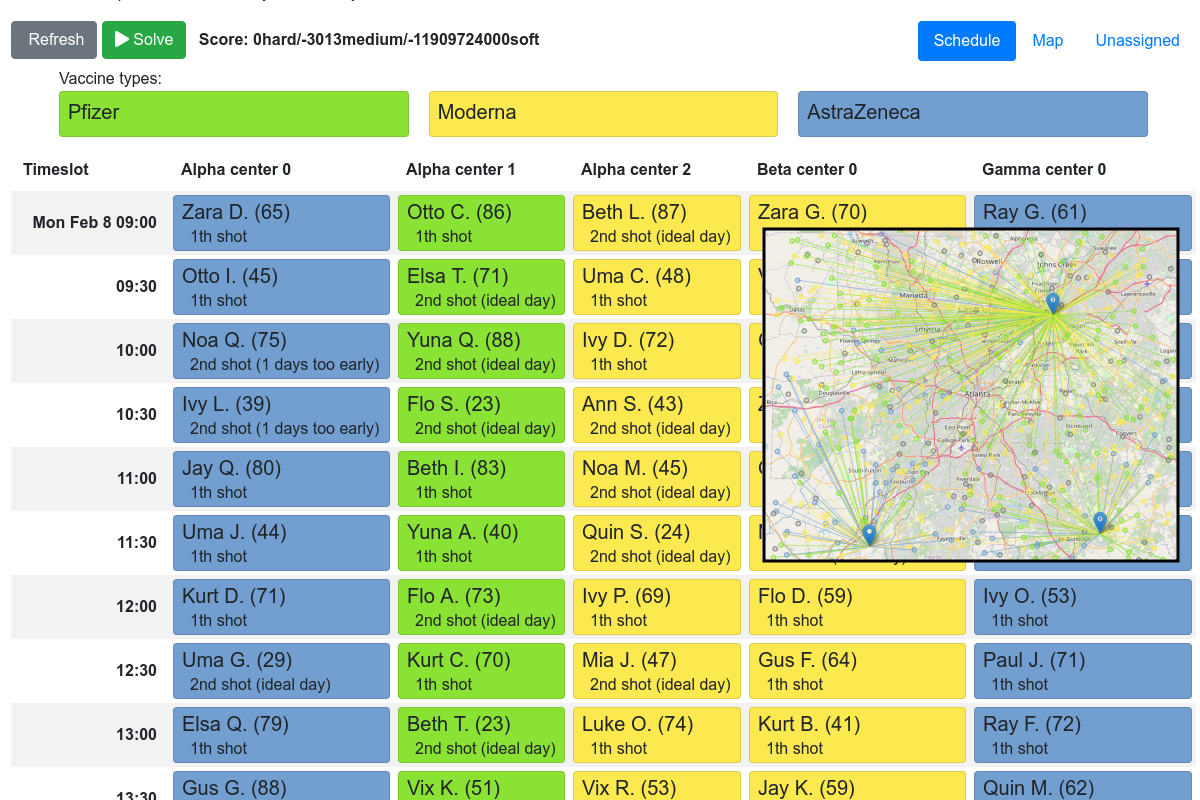
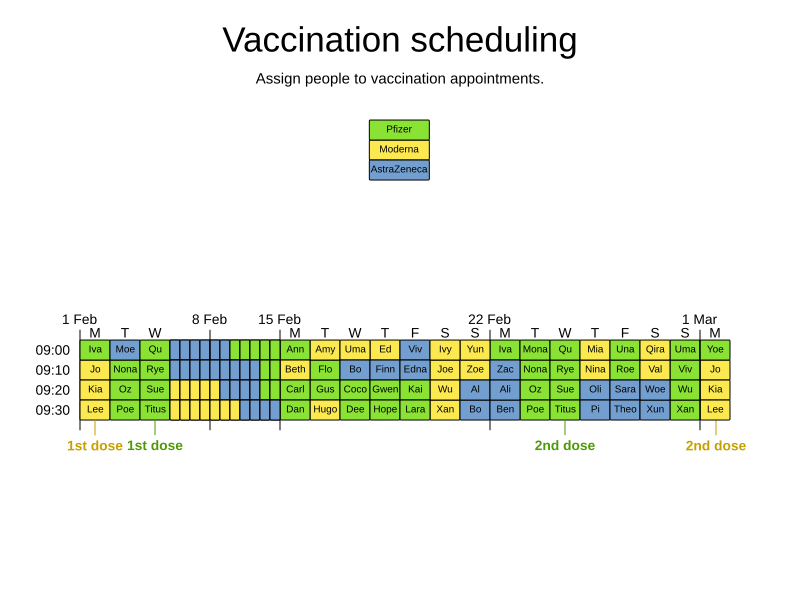
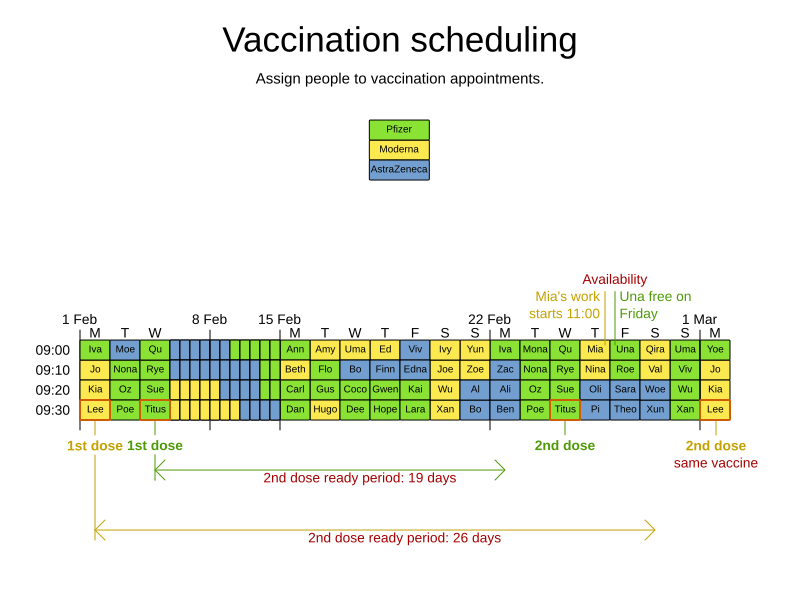
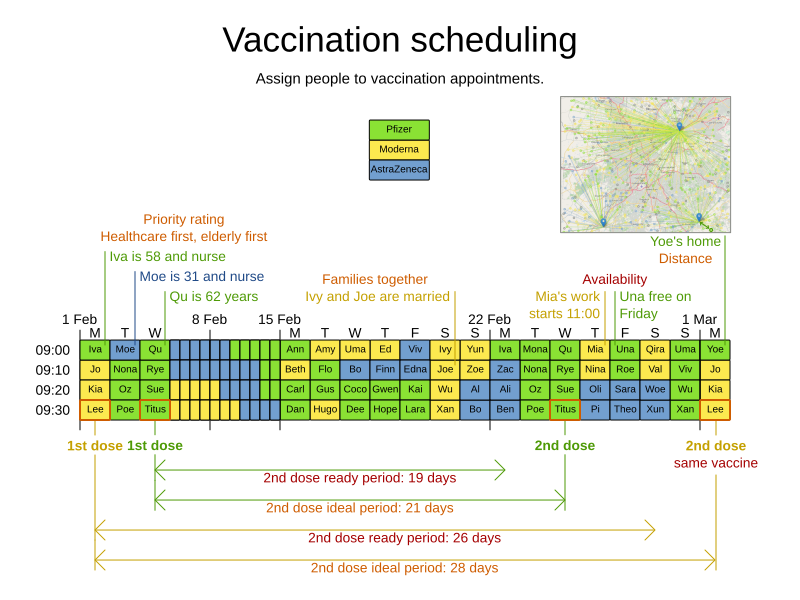
Goals and constraints
- Maximize vaccination throughput
- Don't waste vaccines
- 1 Pfizer bottle = 6 people within 4 hours
- Vaccination center capacity
- Don't waste vaccines
- 2th shot
- Same vaccine
- 21/28 days later
- Elderly and priority groups first
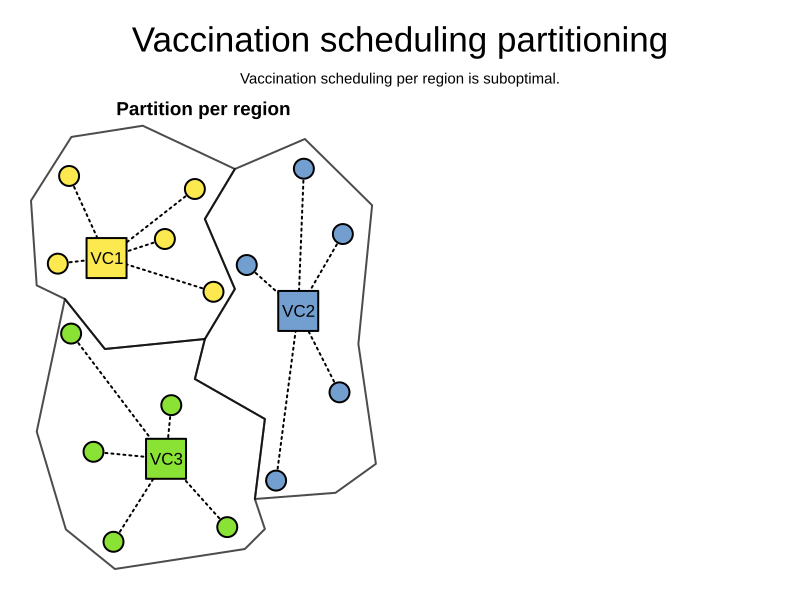
- Minimize driving distance
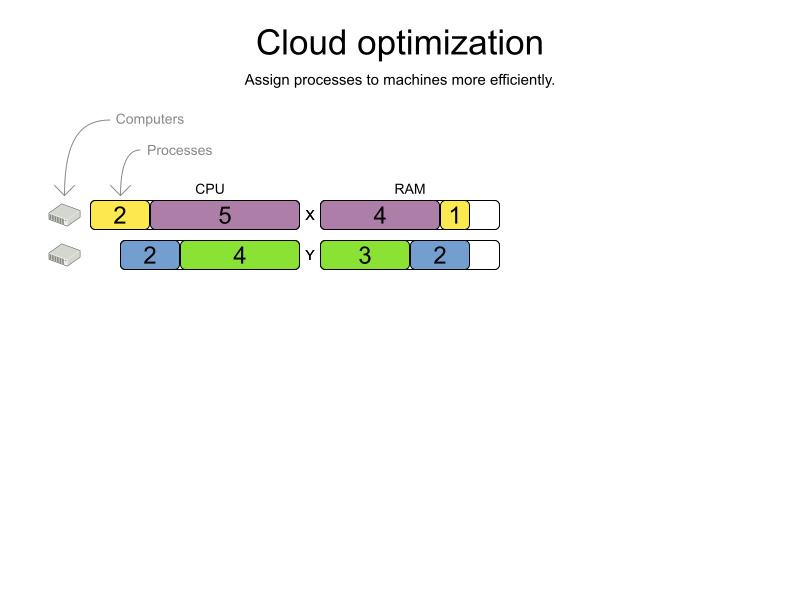
Cloud optimization
Press down to show
Press right to skip
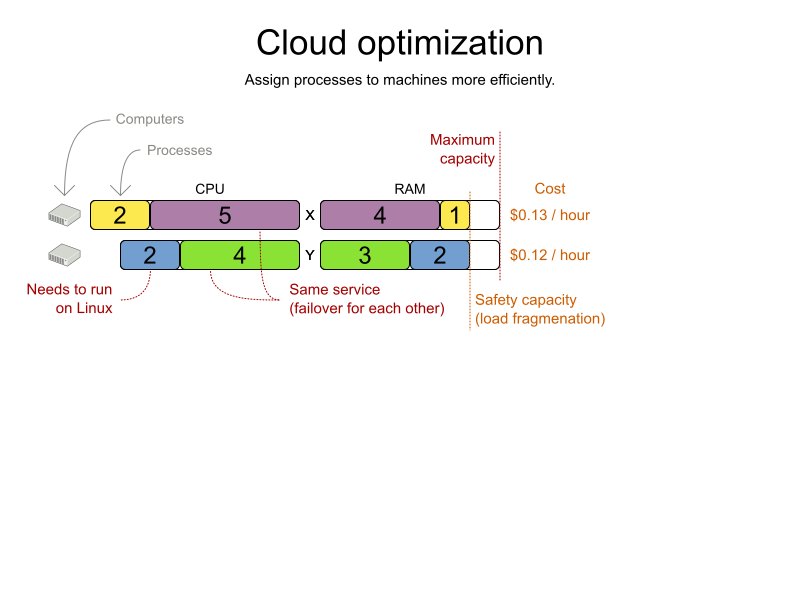
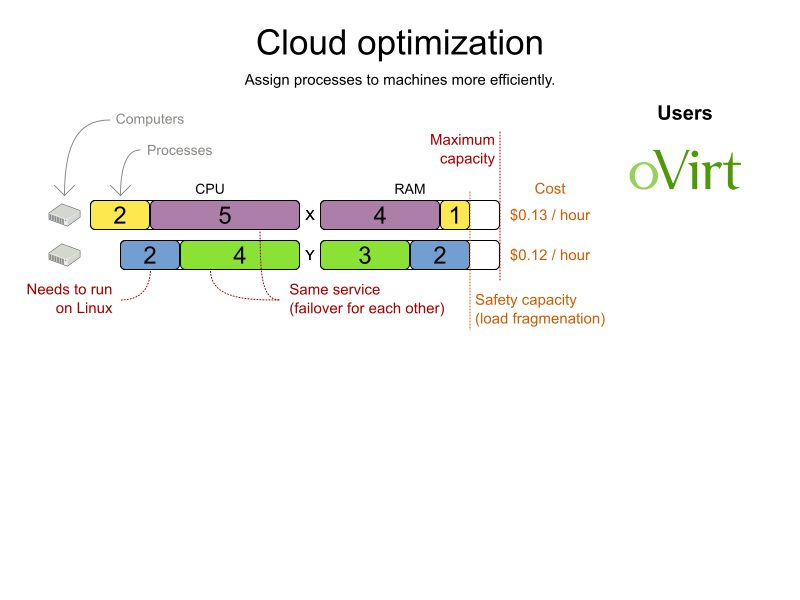
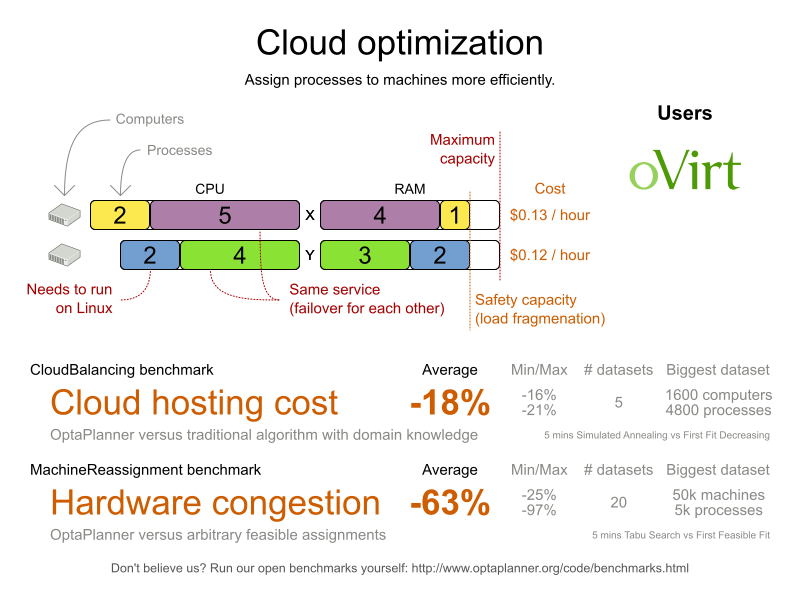
What is constraint solving?

Cloud Balancing demo
Are planning problems
difficult to solve?
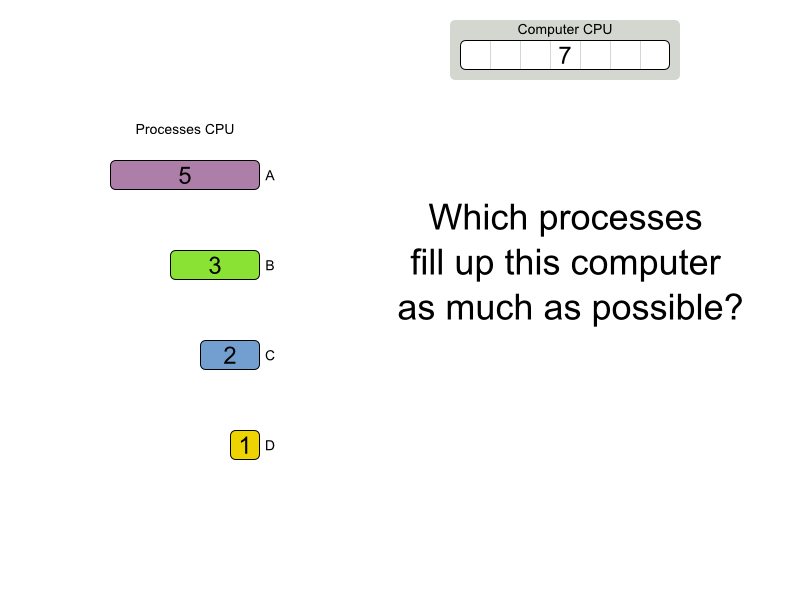
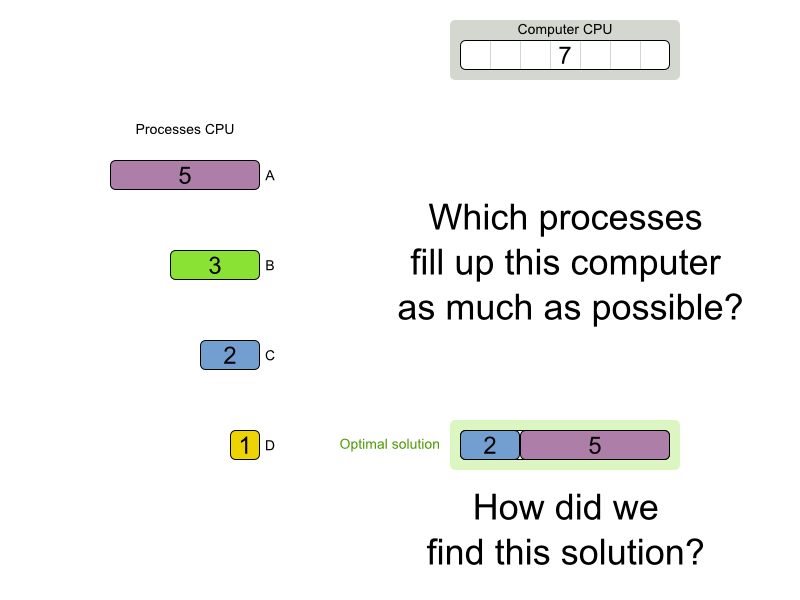

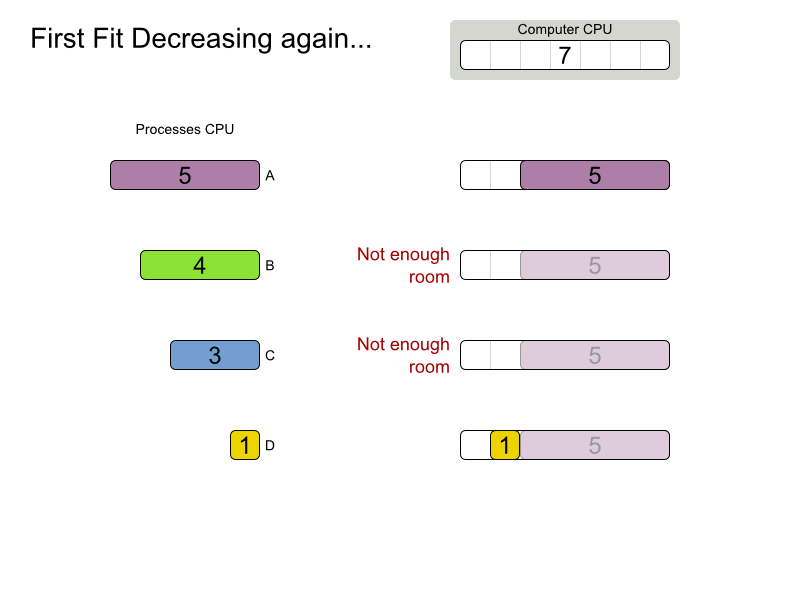
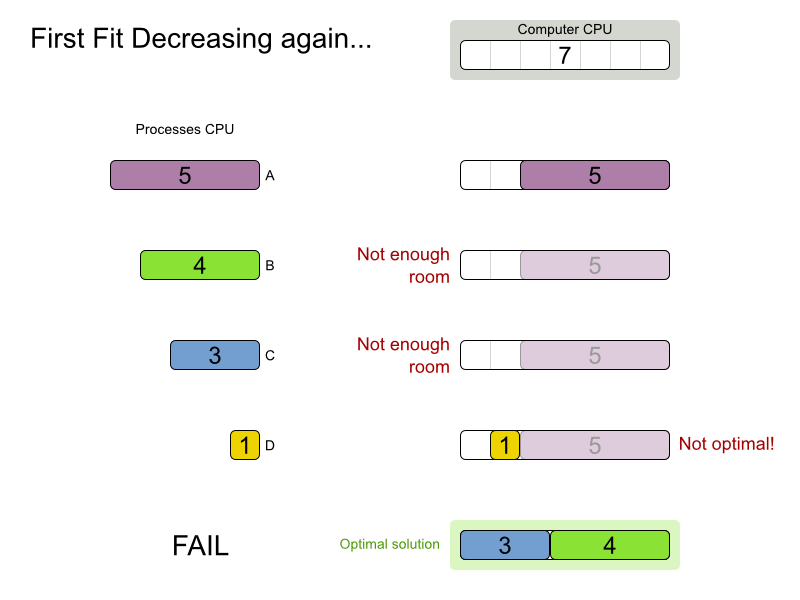
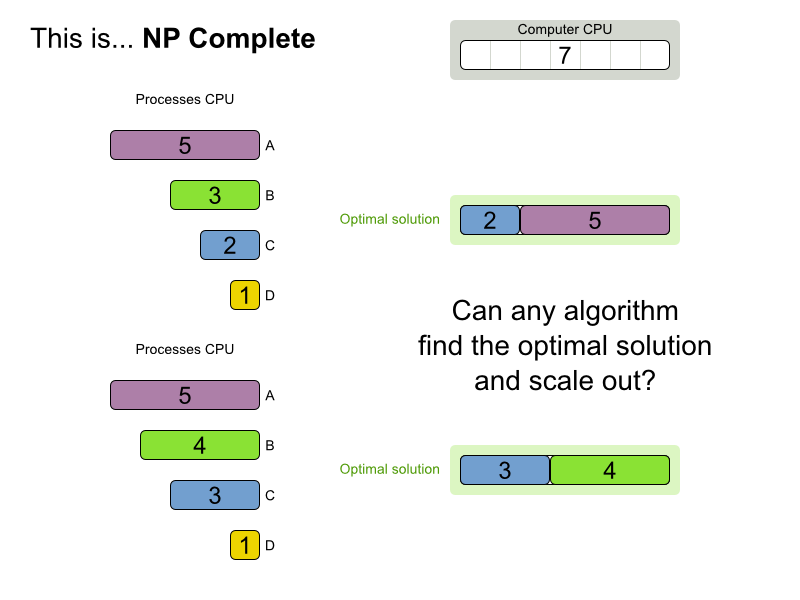
Find optimal solution and scale out
for an NP-complete problem?
⇔ Is P = NP?
- Unresolved since 1971
- 1 000 000 $ reward since 2000
- One of the 7 Millennium Problems
- Most believe P ≠ NP
- ⇔ Impossible to find optimal solution and scale out
- 3000+ known NP-complete problems (wikipedia)
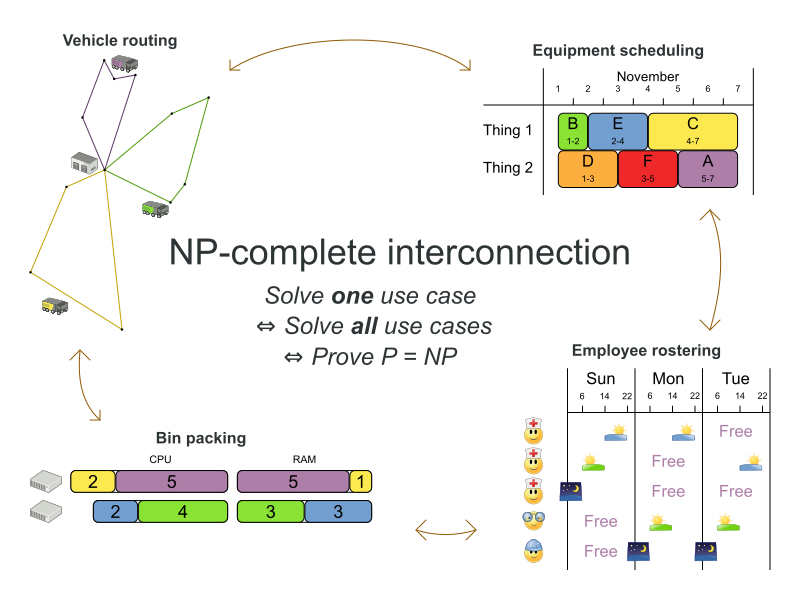
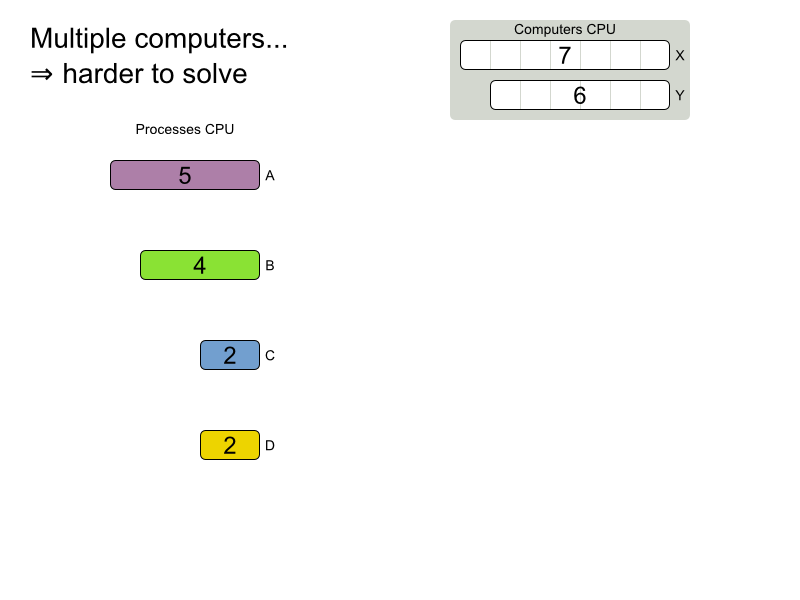
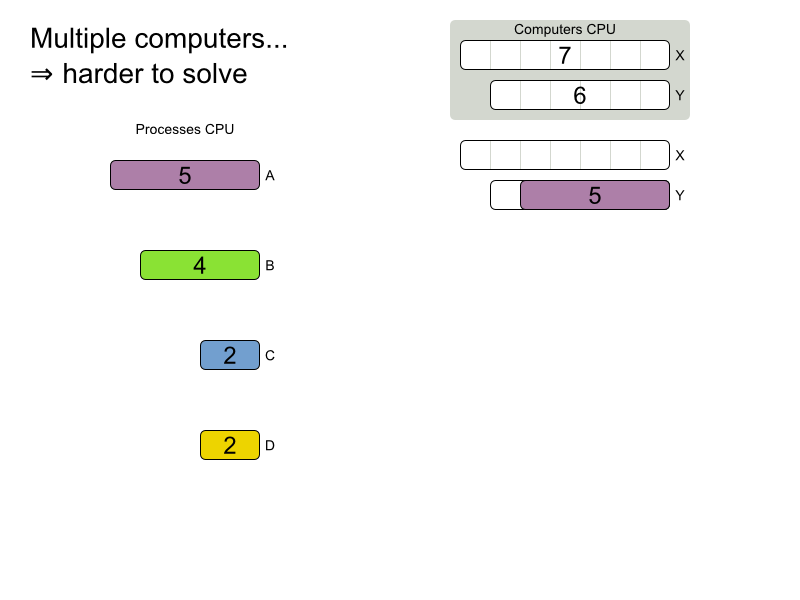
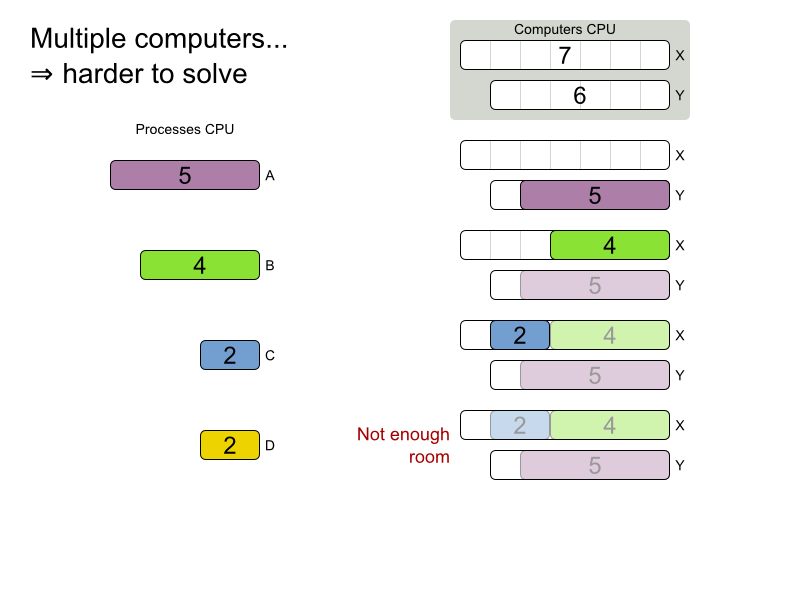
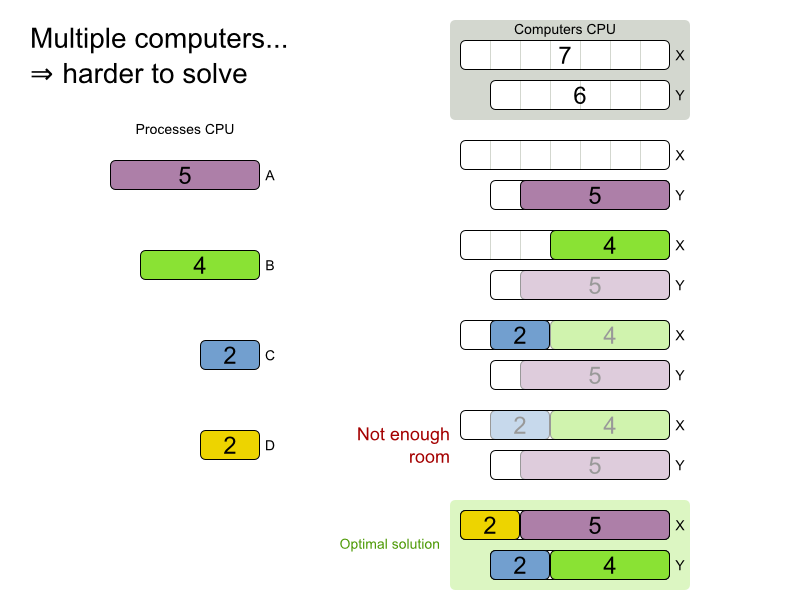
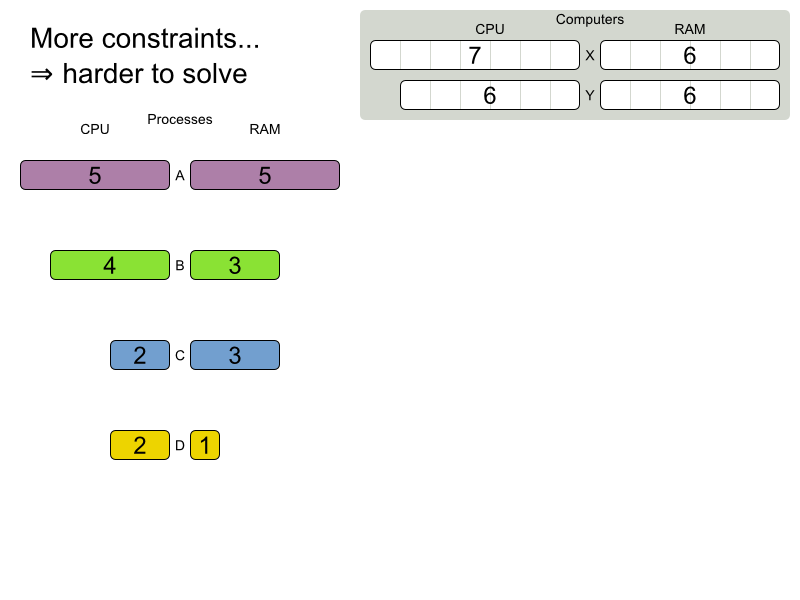
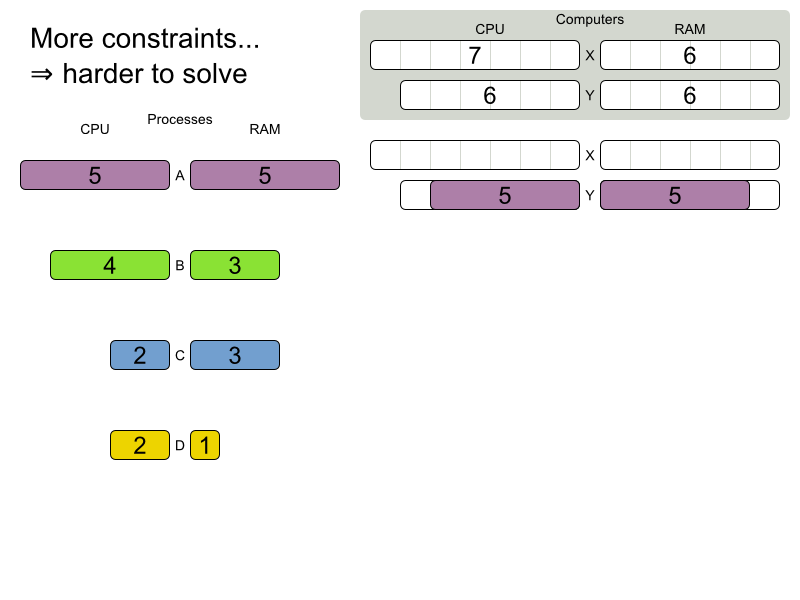
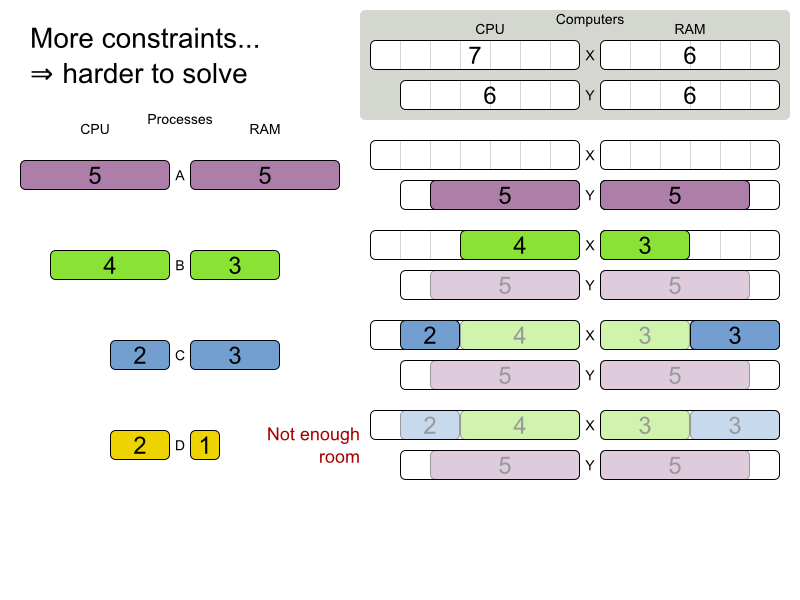
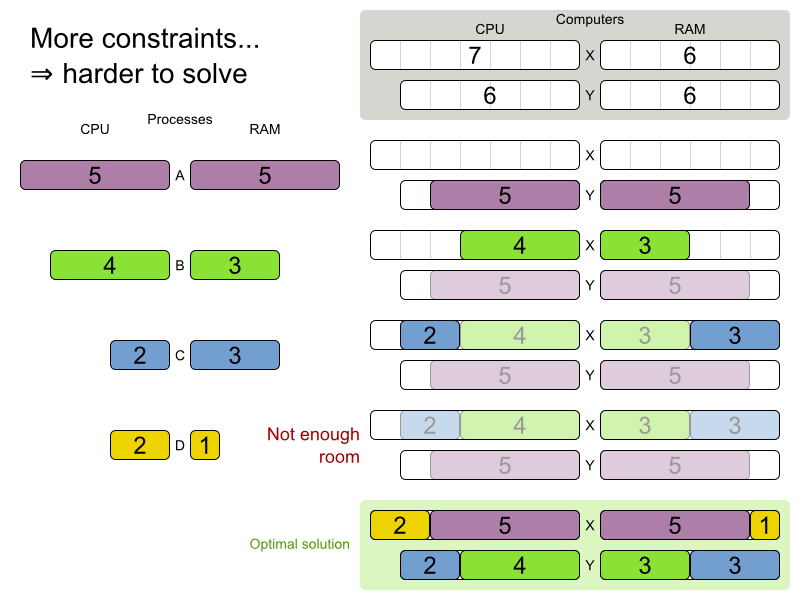
Planning problems are
difficult to solve!
And human aren't good at it

But they don't realize it
(nor does their manager)
Cloud Balancing example
Domain model
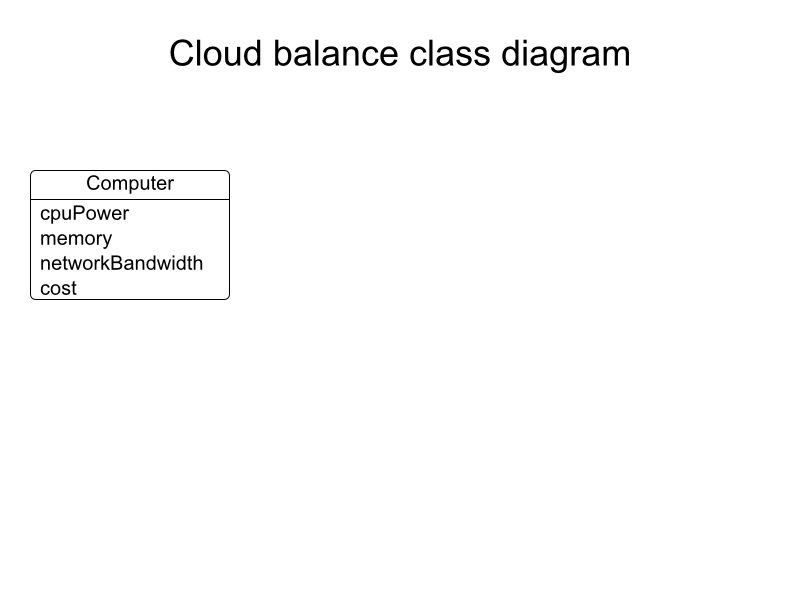
Computer
public class Computer {
private int cpuPower;
private int memory;
private int networkBandwidth;
private int cost;
// getters
}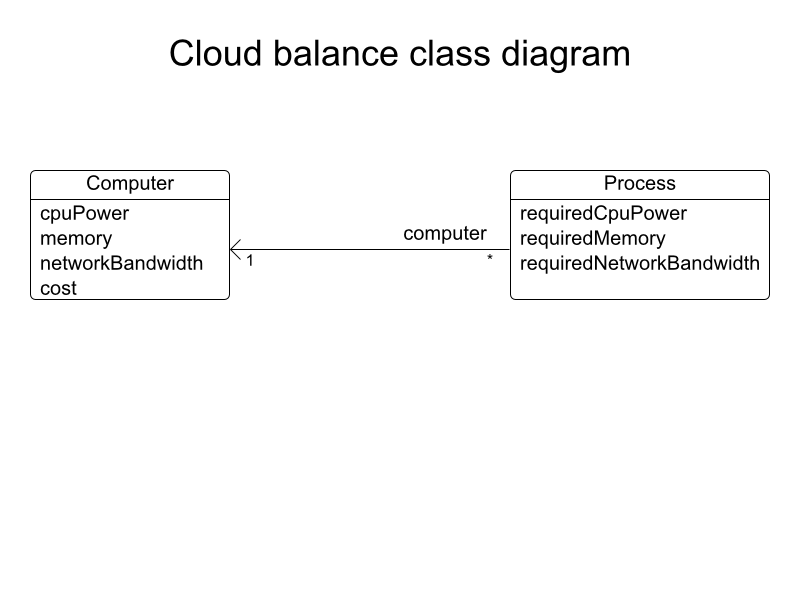
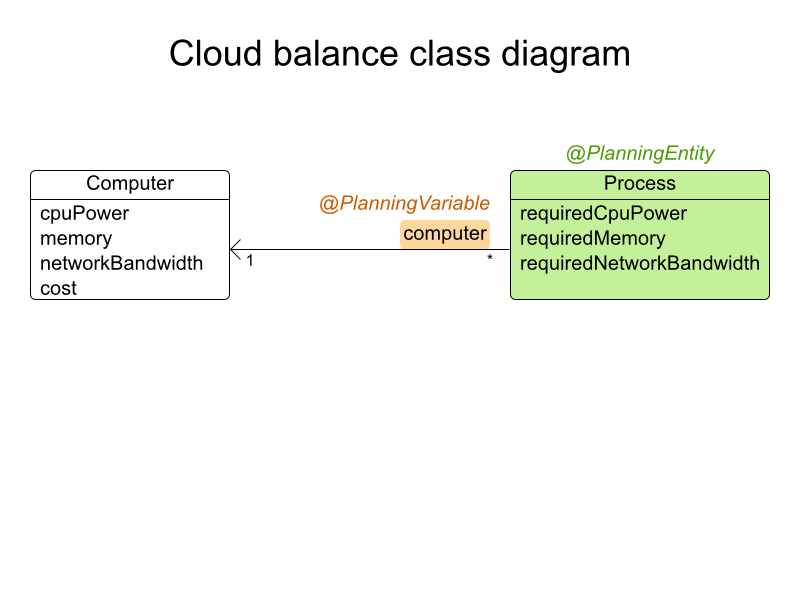
Process is a planning entity
@PlanningEntity
public class Process {
private int requiredCpuPower;
private int requiredMemory;
private int requiredNetworkBandwidth;
// getters
...
}Process has a planning variable
@PlanningEntity
public class Process {
...
private Computer computer;
@PlanningVariable(valueRangeProviderRefs = {"computerRange"})
public Computer getComputer() {
return computer;
}
public void setComputer(Computer computer) {
this.computer = computer;
}
}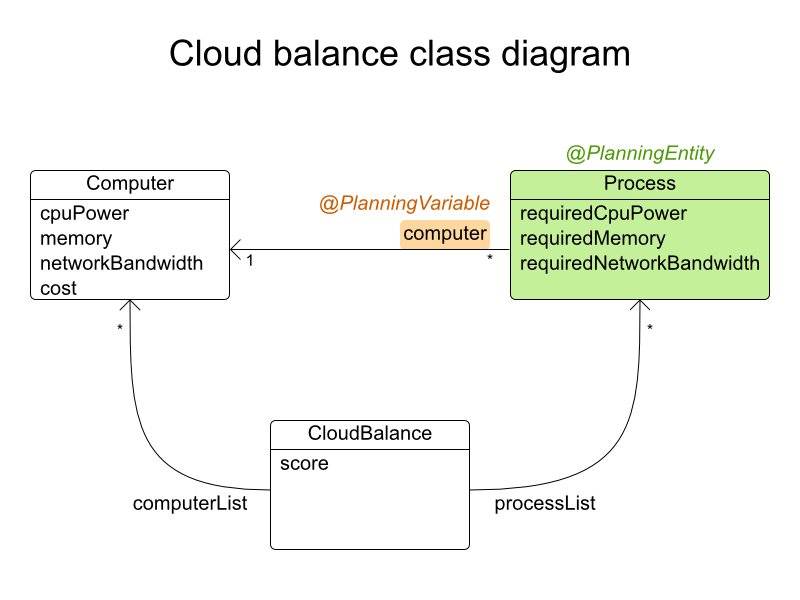
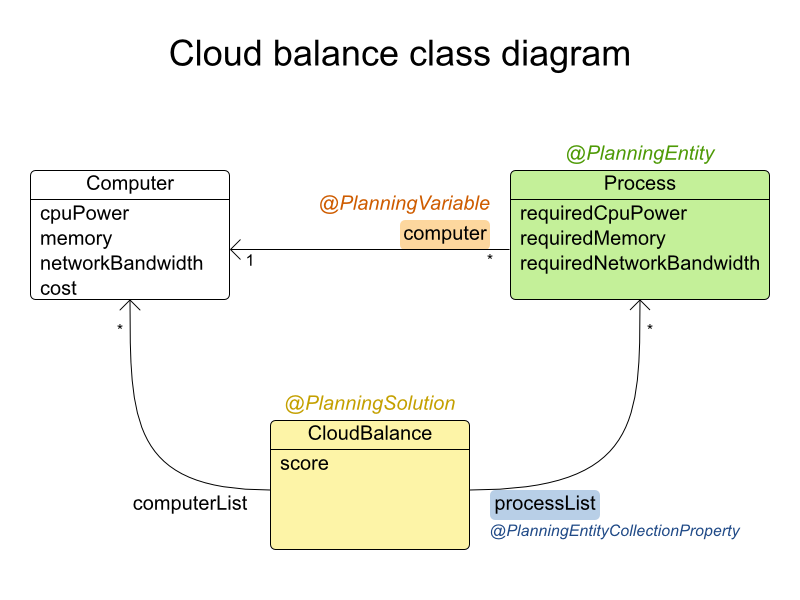
Solution CloudBalance
@PlanningSolution
public class CloudBalance {
private List<Computer> computerList;
private List<Process> processList;
@ValueRangeProvider(id = "computerRange")
@ProblemFactCollectionProperty
public List<Computer> getComputerList() {
return computerList;
}
@PlanningEntityCollectionProperty
public List<Process> getProcessList() {
return processList;
}
...
}Solution CloudBalance: score
@PlanningSolution
public class CloudBalance {
...
private HardSoftScore score;
@PlanningScore
public HardSoftScore getScore() {
return score;
}
public void setScore(HardSoftScore score) {
this.score = score;
}
}
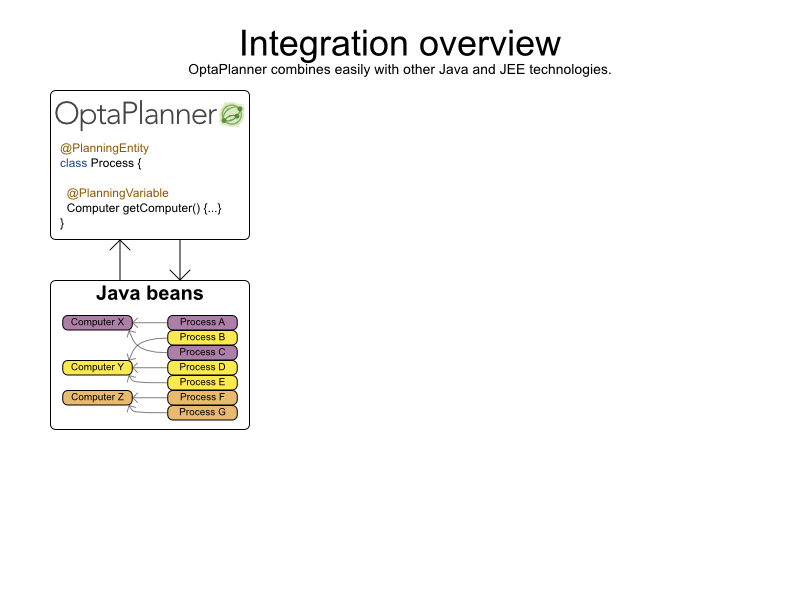
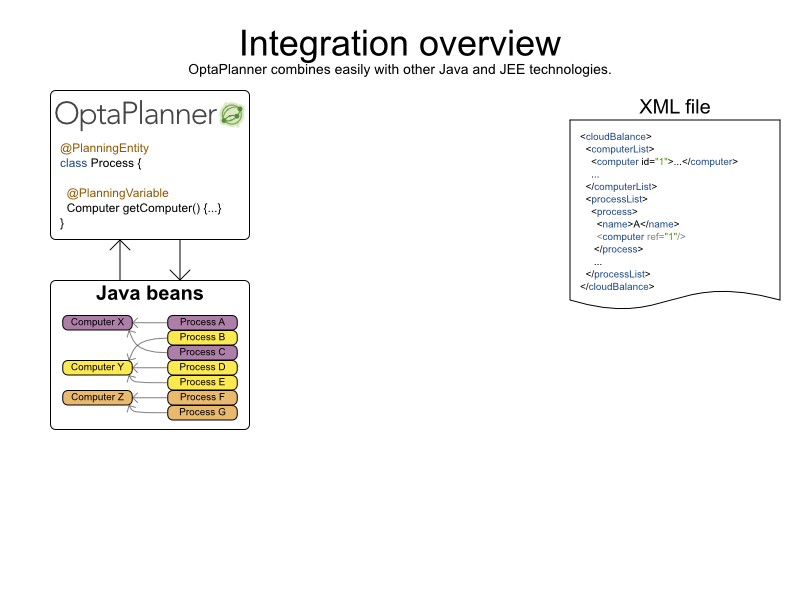
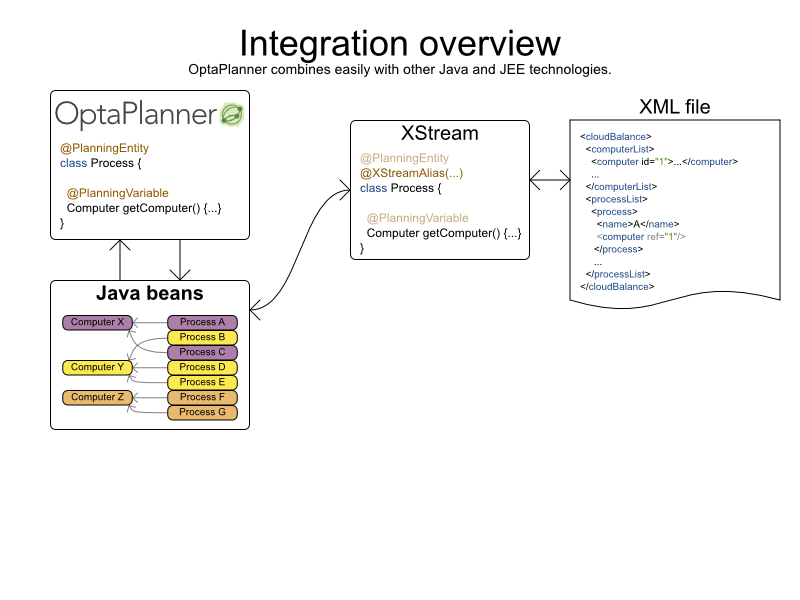
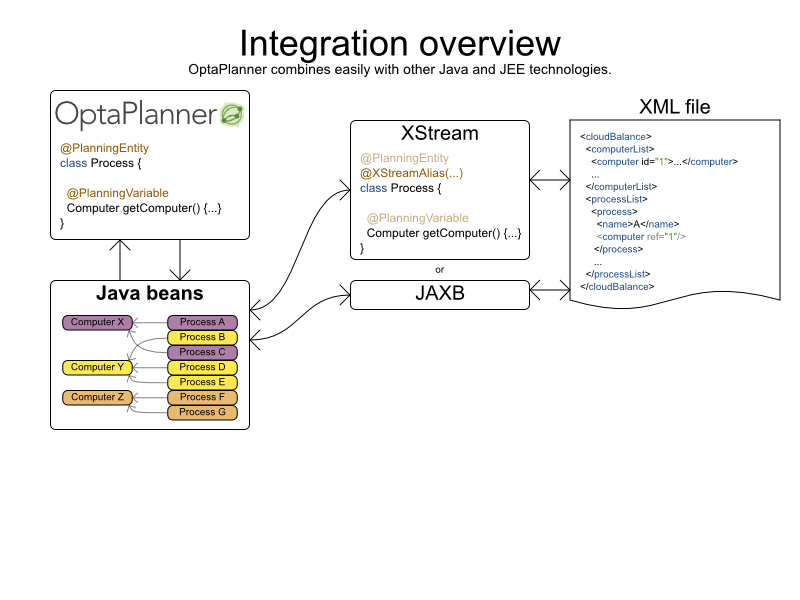
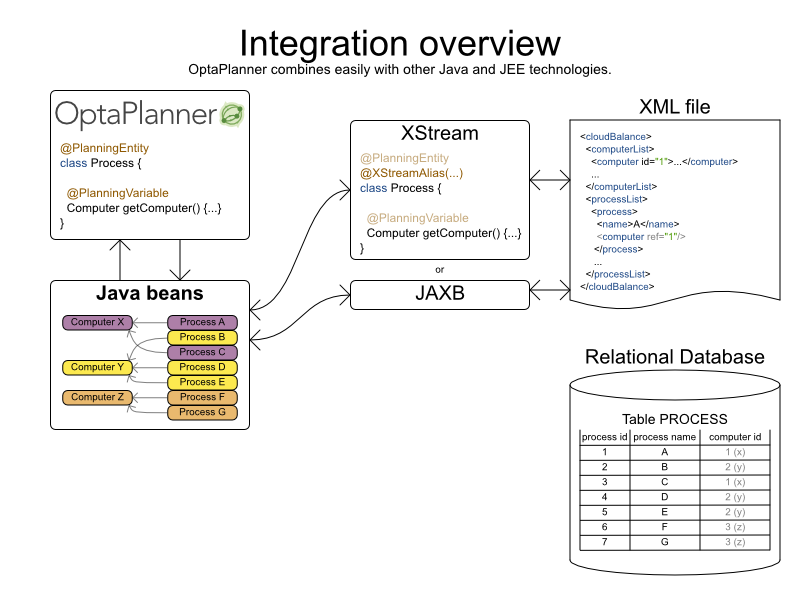
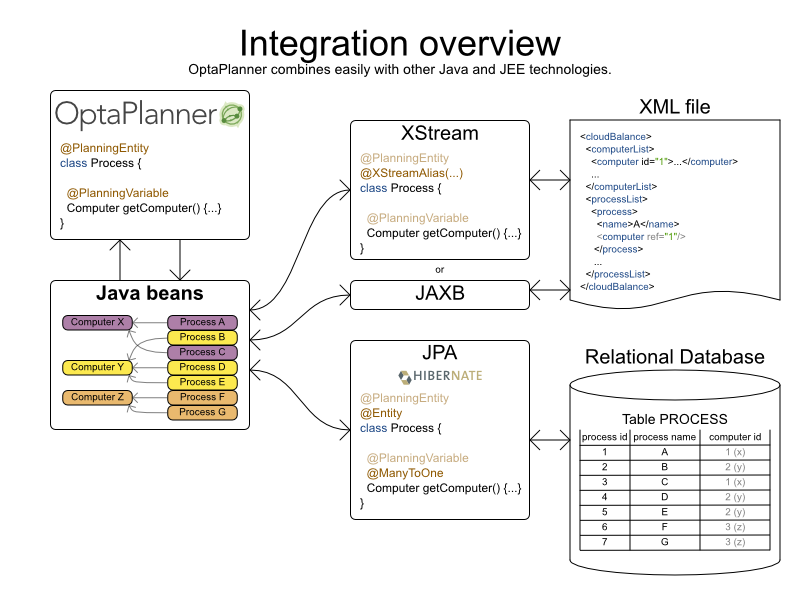
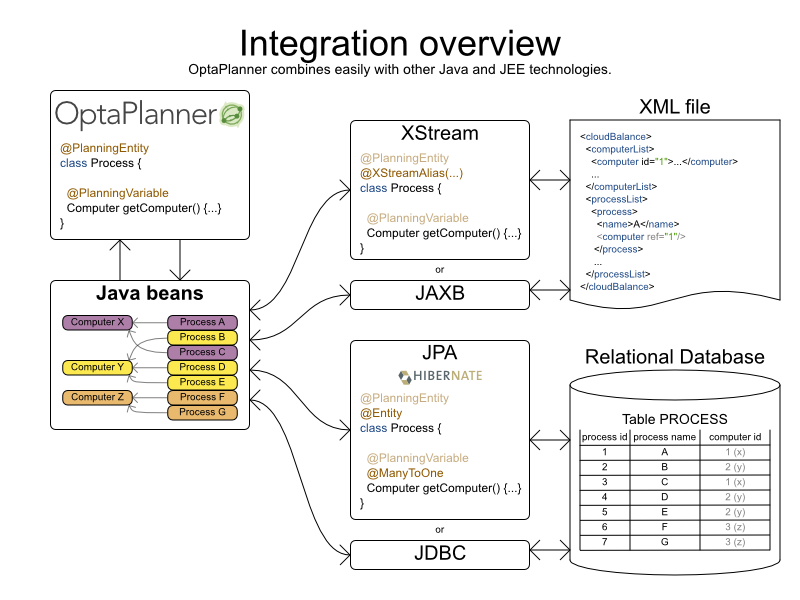
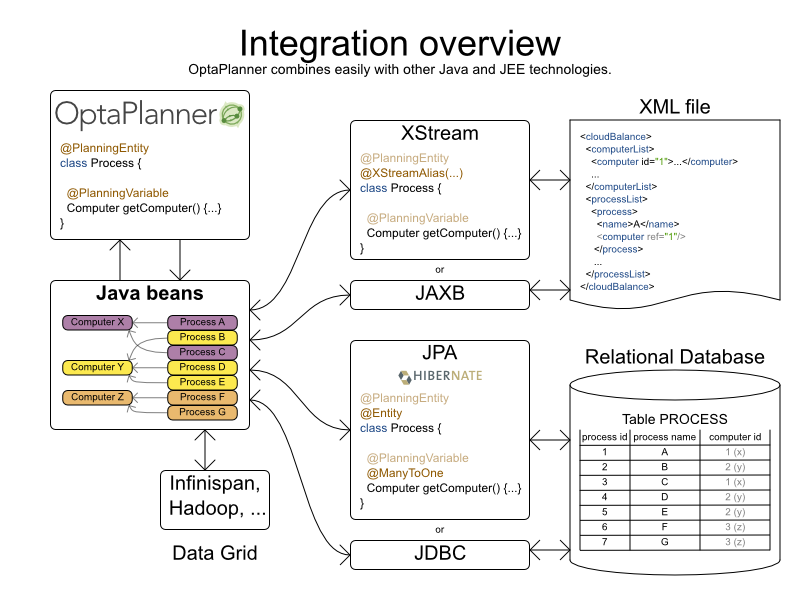
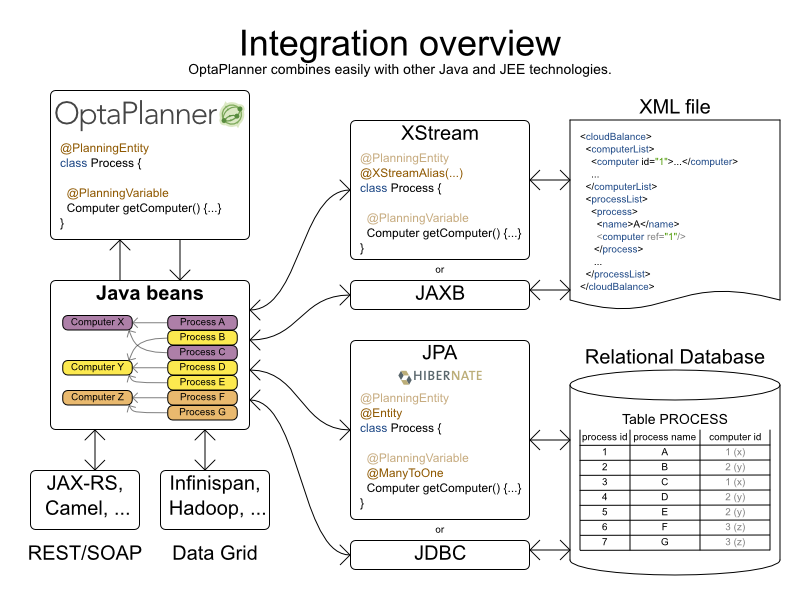
Cloud Balancing example
Score constraints
Given 2 solutions
which one is better?

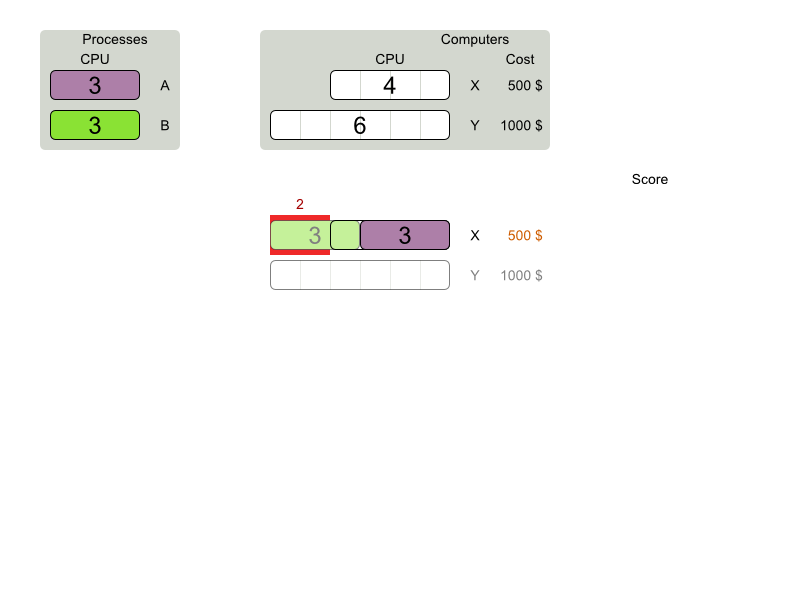
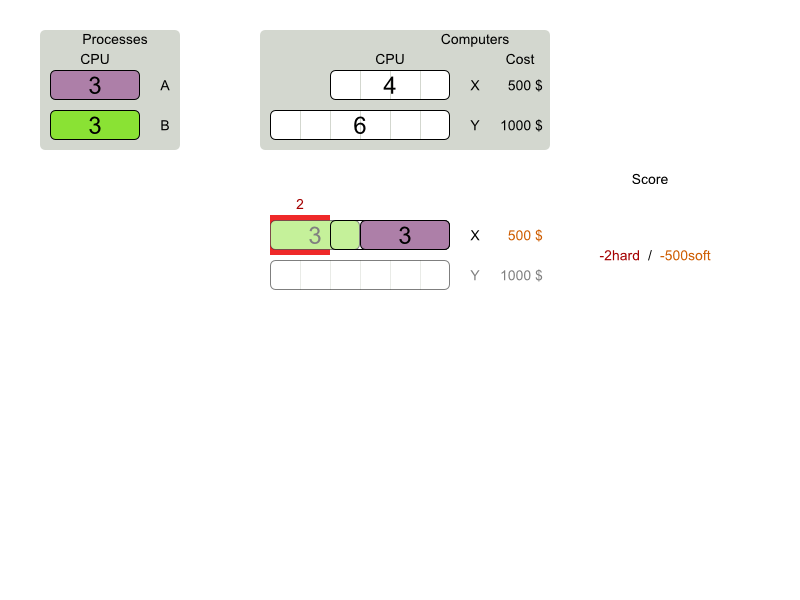
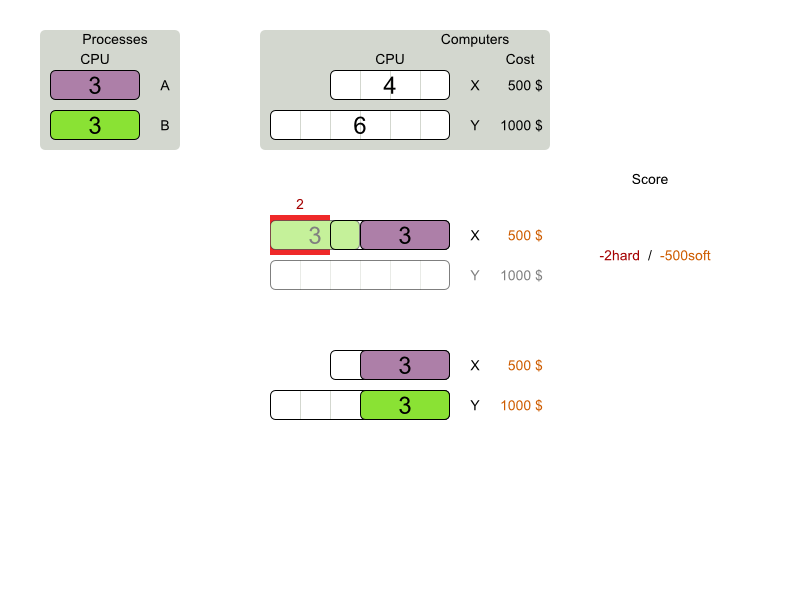
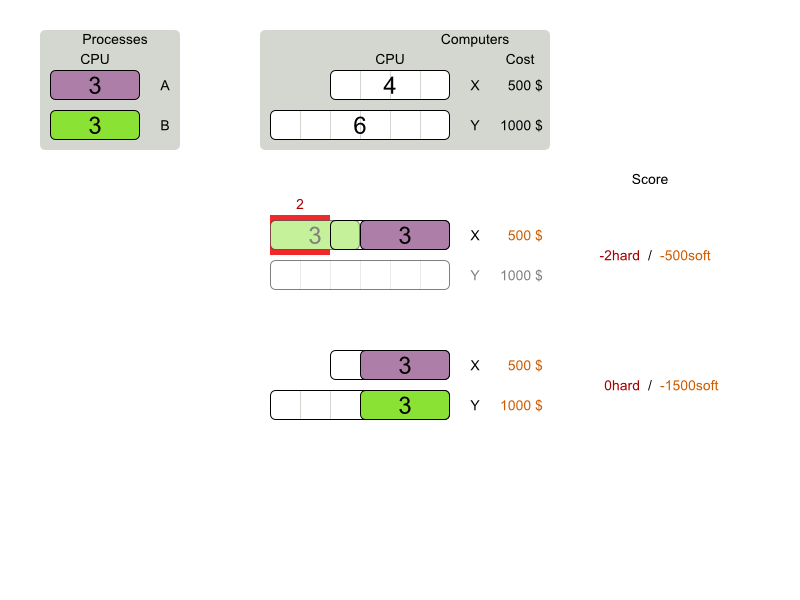
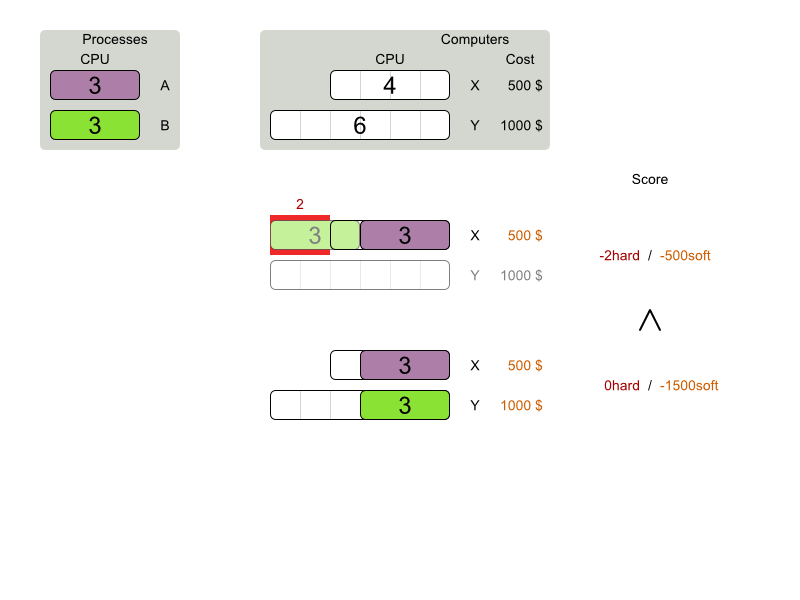
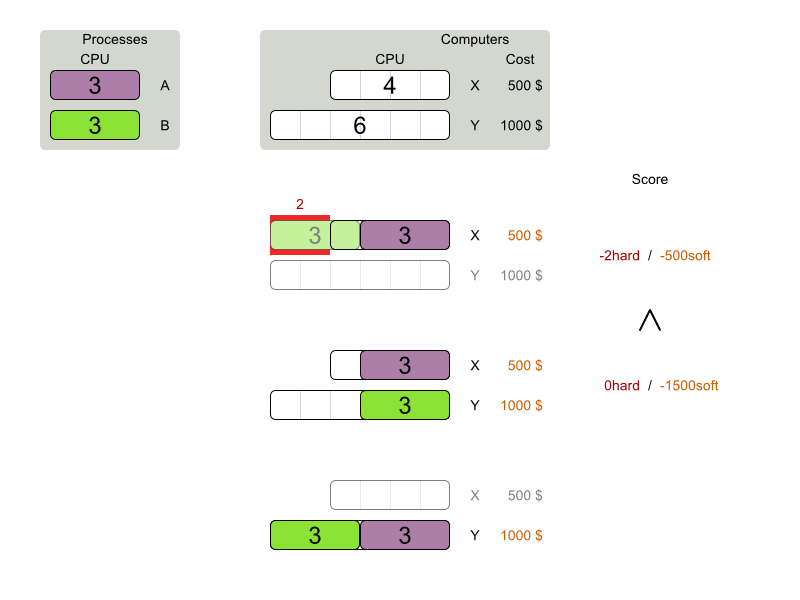
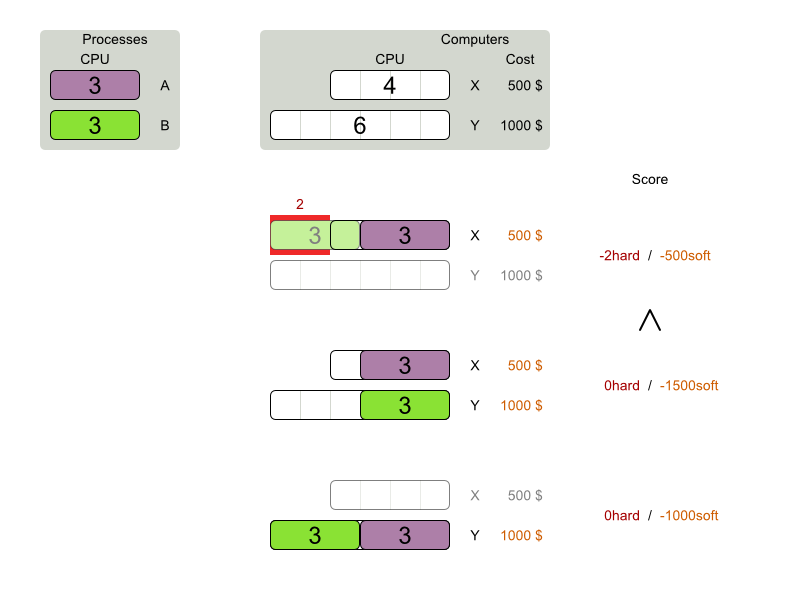
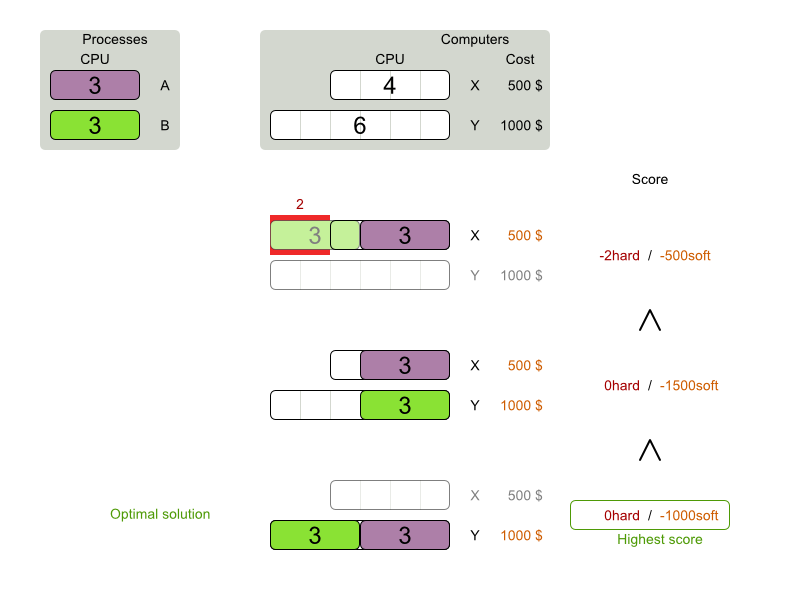
Score calculation
- Easy Java
- Incremental Java
- Drools
Easy Java score calculation
- Easy to implement
- Bridge an existing system
- Slow
public class CloudBalancingEasyScoreCalculator
implements EasyScoreCalculator<CloudBalance> {
public HardSoftScore calculateScore(CloudBalance cb) {
...
return HardSoftScore.valueOf(hardScore, softScore);
}
}Incremental Java score calculation
- Fast
- Solution changes ⇒ recalculate score delta only
- Hard to implement
- Much boilerplate code
Drools score calculation
- Incremental
- No boilerplate code
- Constraints in Drools Rule Language (DRL)
- Declarative (like SQL, regular expression)
- Integration opportunities
- Drools Workbench
- Decision tables
DRL soft constraint: computer cost
rule "computerCost"
when
// there is a computer
$s : Computer($c : cost)
// there is a processes on that computer
exists Process(computer == $s)
then
// lower soft score by the maintenance cost
scoreHolder.addSoftConstraintMatch(kcontext, - $c);
endDRL hard constraint: CPU power
rule "requiredCpuPowerTotal"
when
// there is a computer
$s : Computer($cpu : cpuPower)
// with too little cpu for its processes
accumulate(
Process(computer == $s, $requiredCpu : requiredCpuPower);
$total : sum($requiredCpu);
$total > $cpu
)
then
// lower hard score by the excessive CPU usage
scoreHolder.addHardConstraintMatch(kcontext,
$cpu - $total);
endScore calculation must be flexible
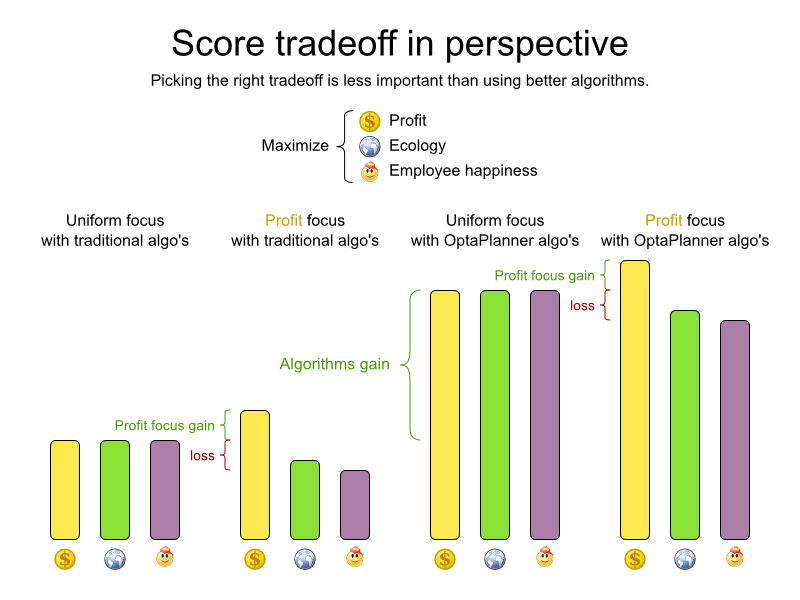
- Optimal solution for almost your business problem is useless
-
Model supports:
- Reusing existing classes
- Rich, OO class hierarchies (including polymorphism)
-
Constraints supports:
- Any constraint (no linear or quadratic restrictions!)
- Reusing existing code
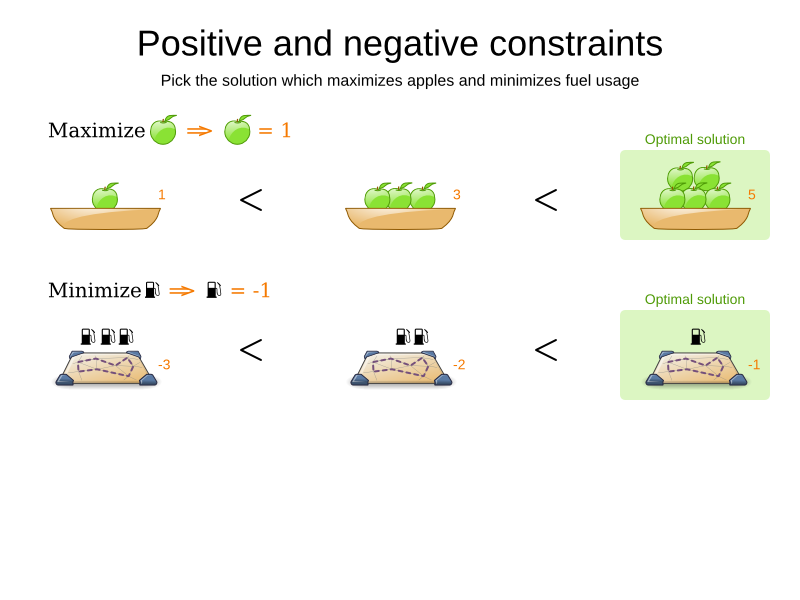
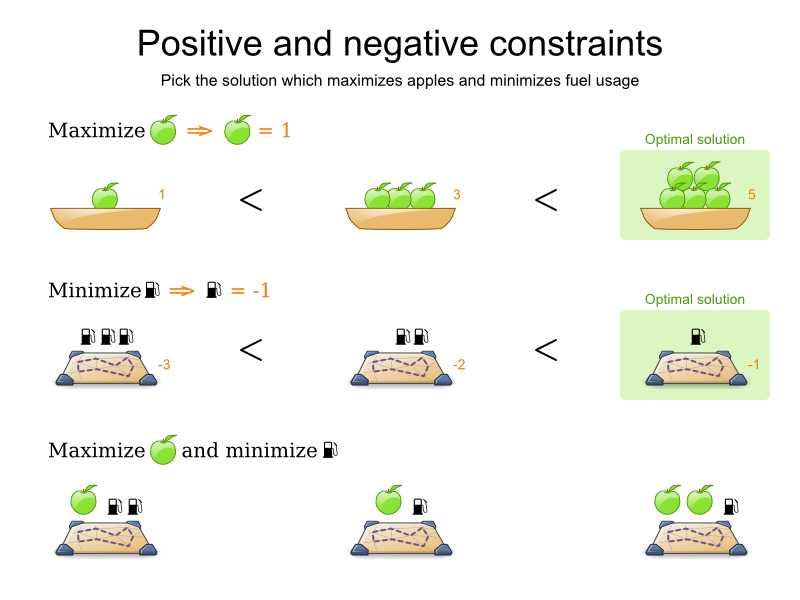
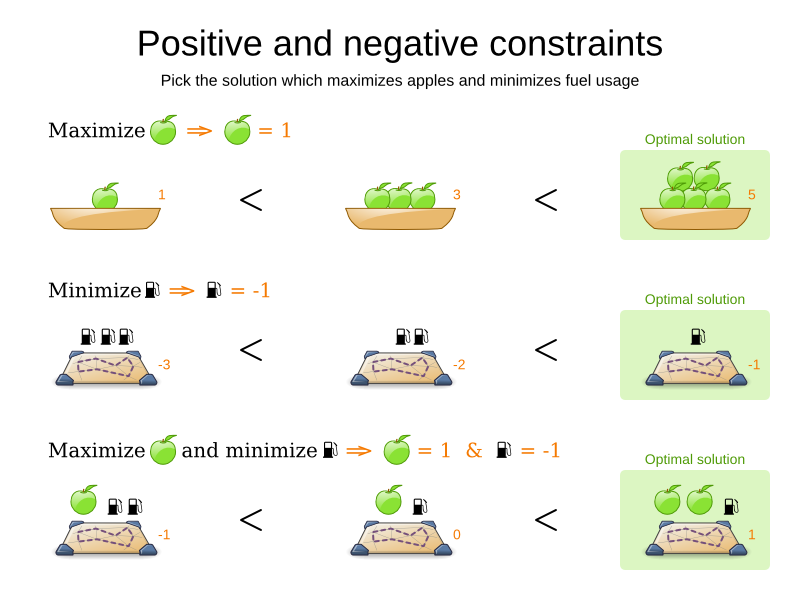
-
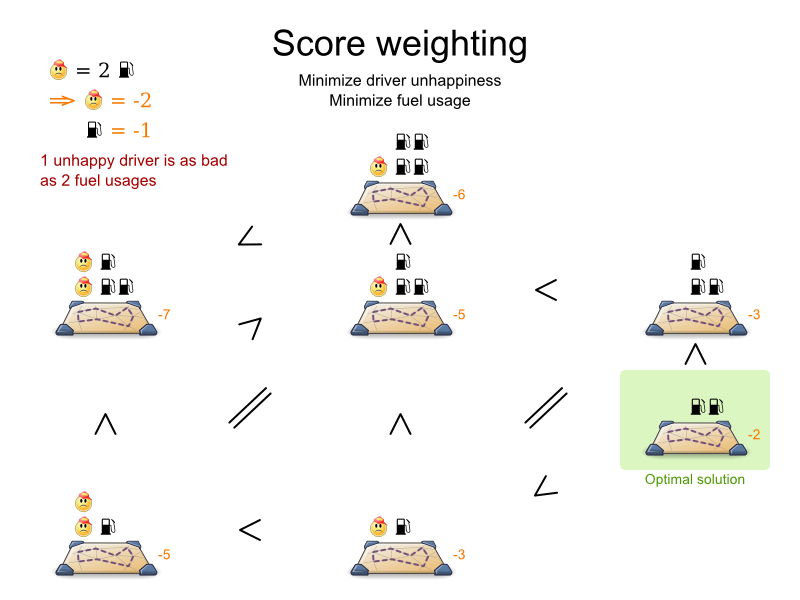
Scoring supports:
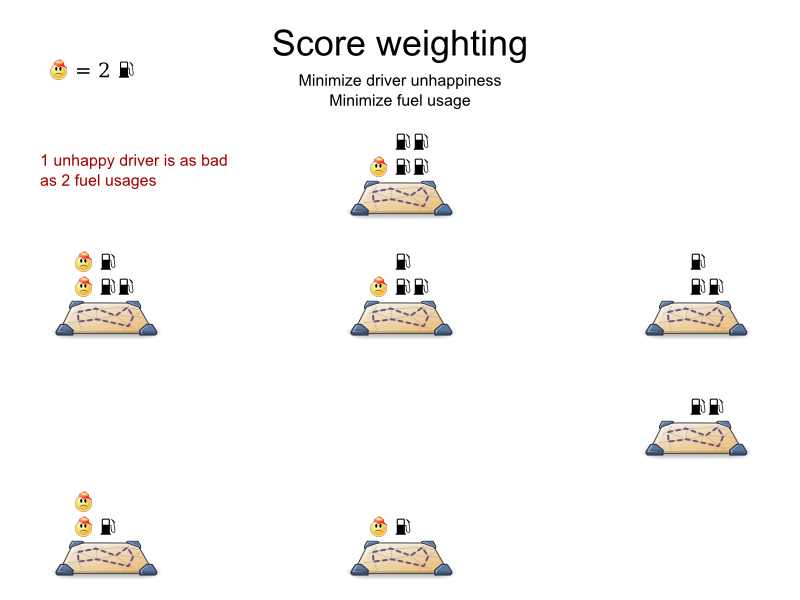
- Positive/negative mix
- Score weights
- Unlimited score levels
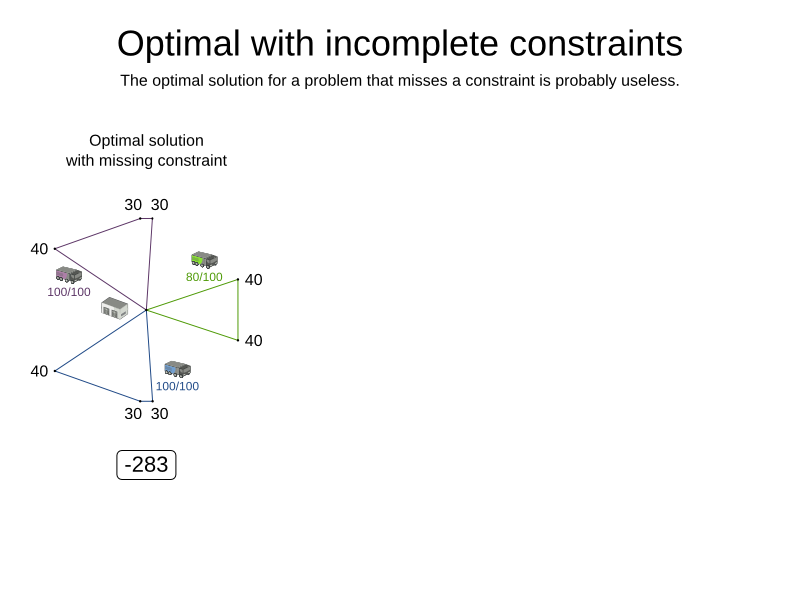
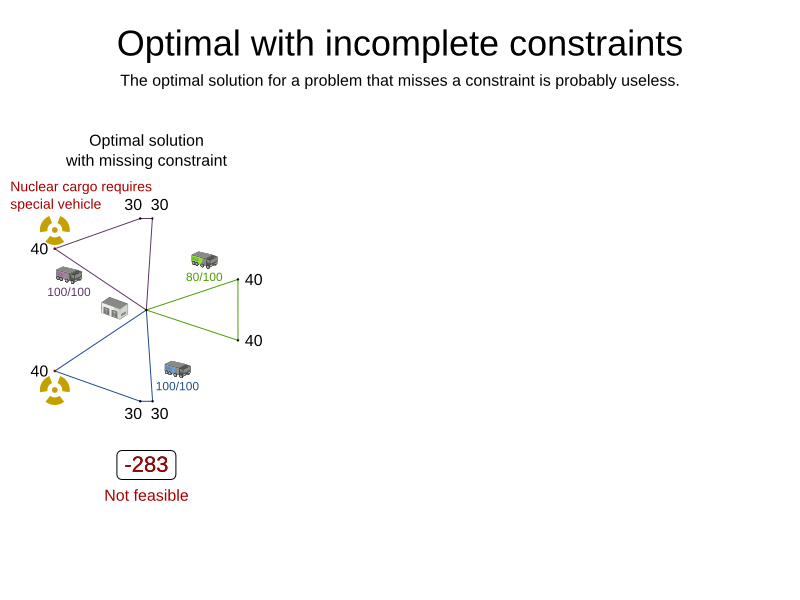
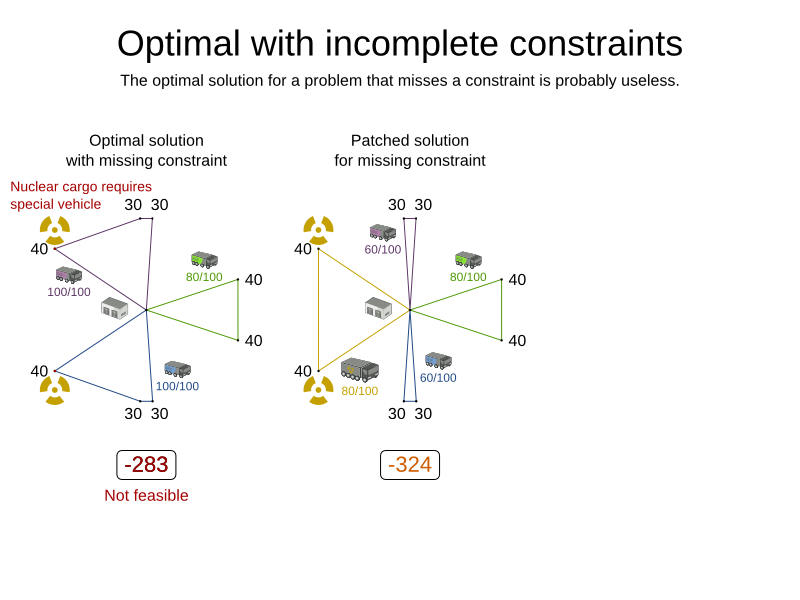
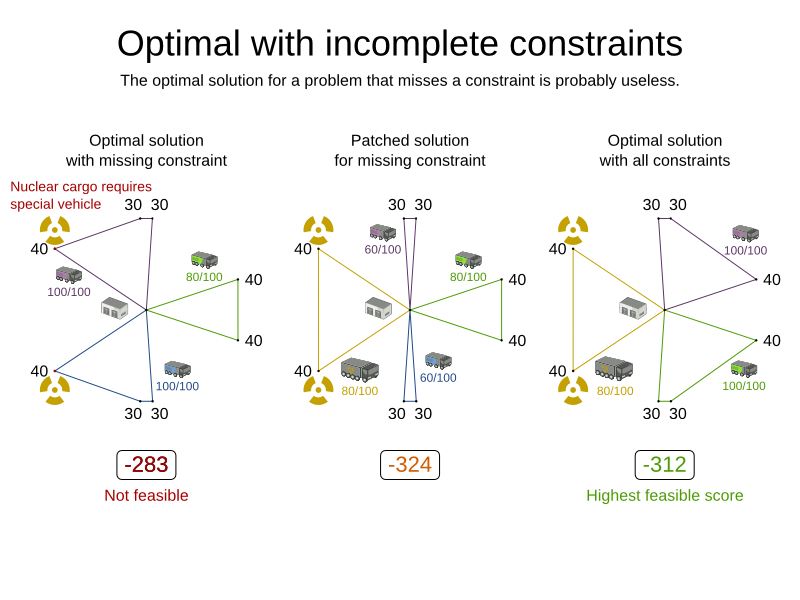
Cloud Balancing example
Solving it
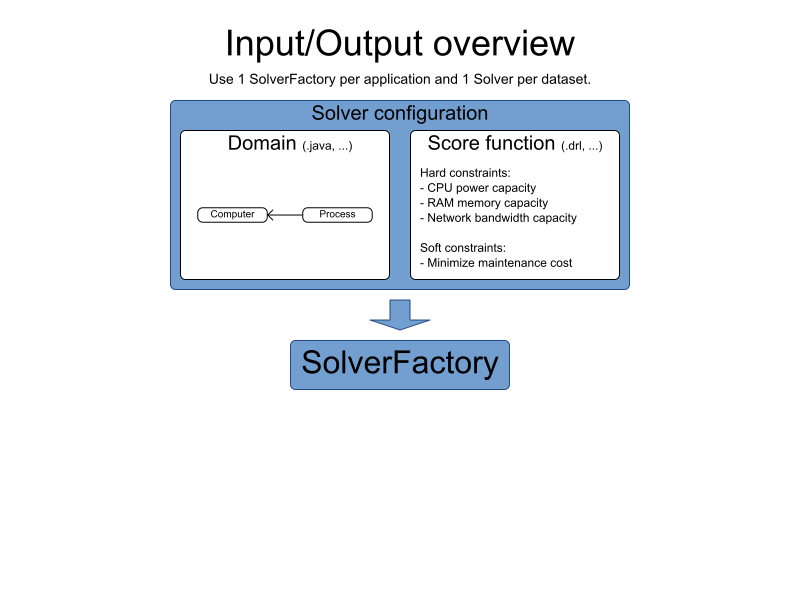
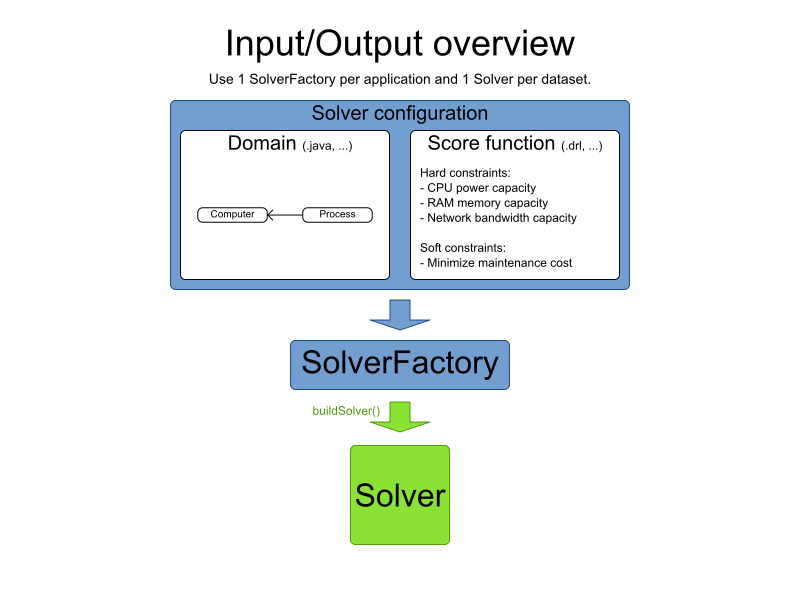
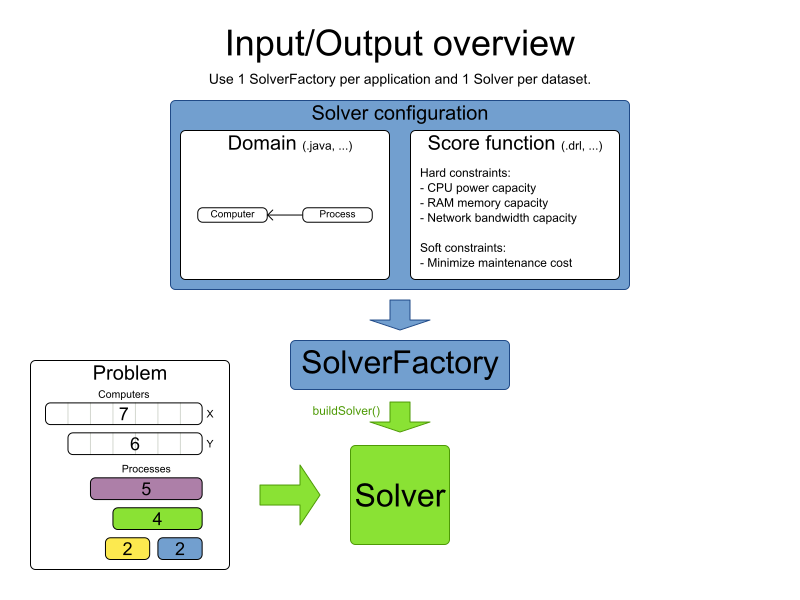
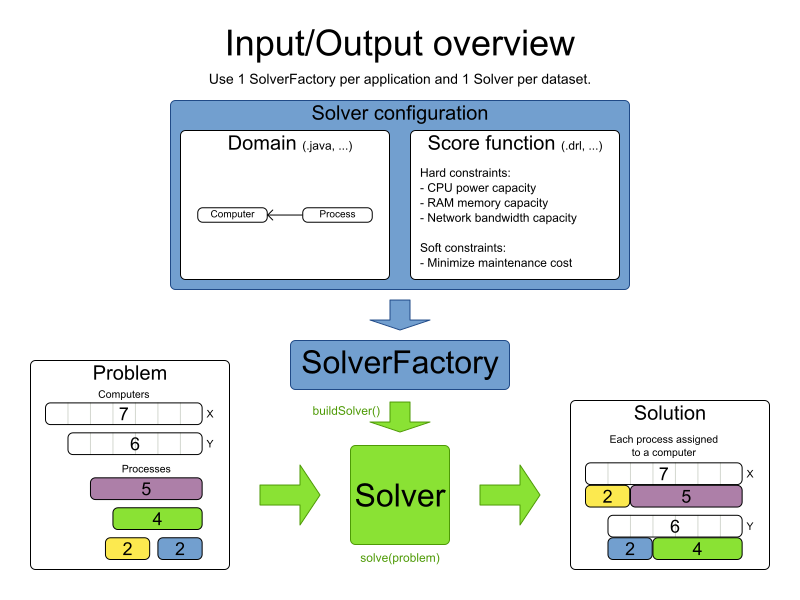
Solver configuration by XML
<solver>
<scanAnnotatedClasses/>
<scoreDirectorFactory>
<scoreDrl>...Constraints.drl</scoreDrl>
</scoreDirectorFactory>
</solver>Solving
SolverFactory<CloudBalance> factory
= SolverFactory.createFromXmlResource("...SolverConfig.xml");
Solver<CloudBalance> solver = factory.buildSolver();
CloudBalance problem = ... // Load problem
CloudBalance solution = solver.solve(problem);Repeated planning


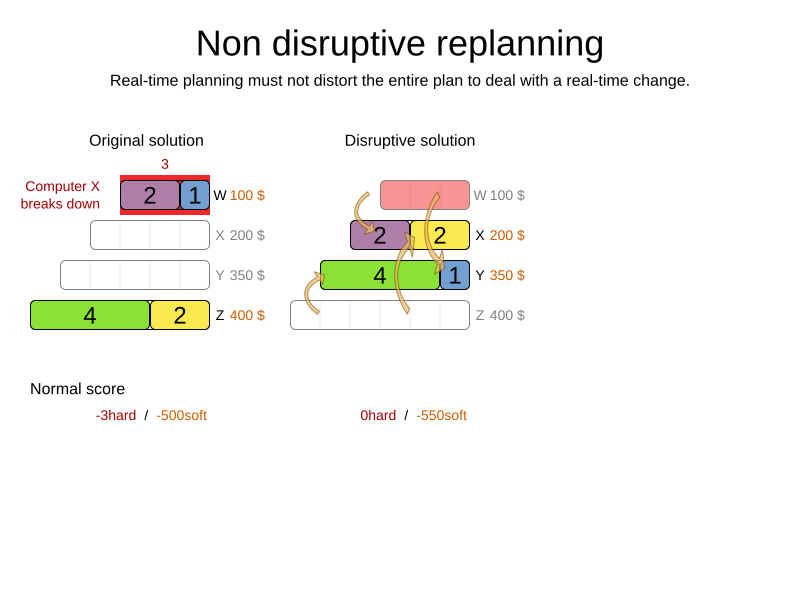
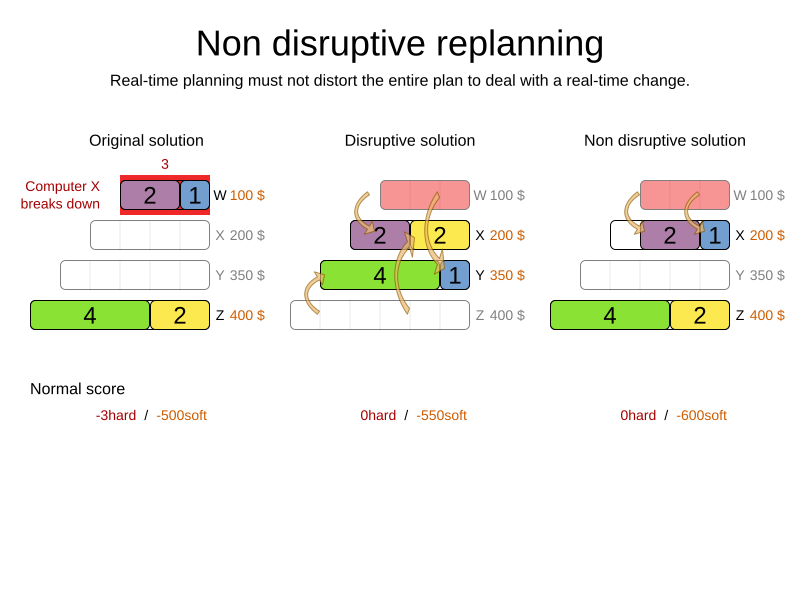
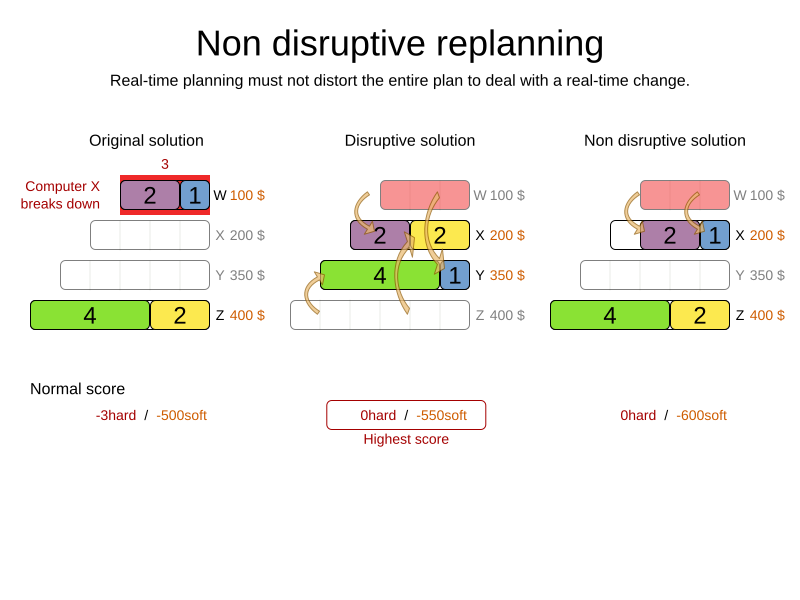
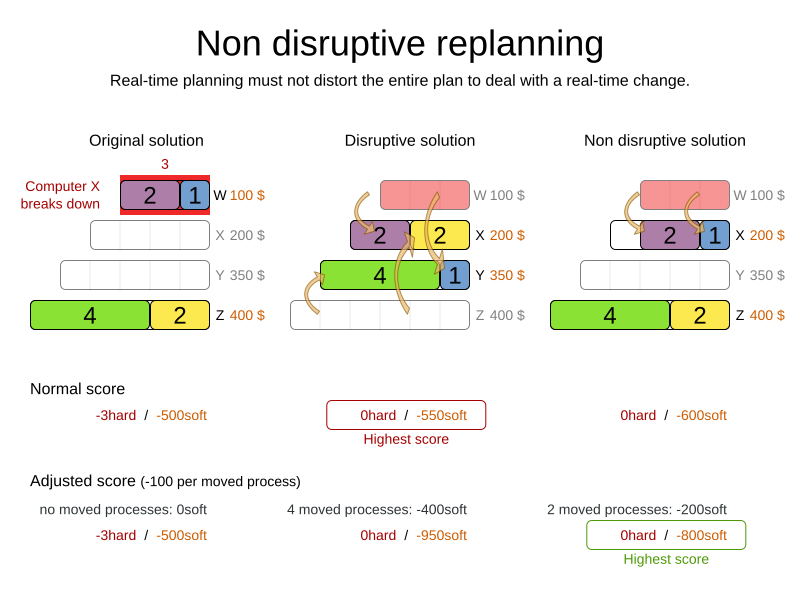
Power tweaking and benchmarking
optimization algorithms
Press down to show
Press right to skip
Cloud Balancing example
Optimization algorithms
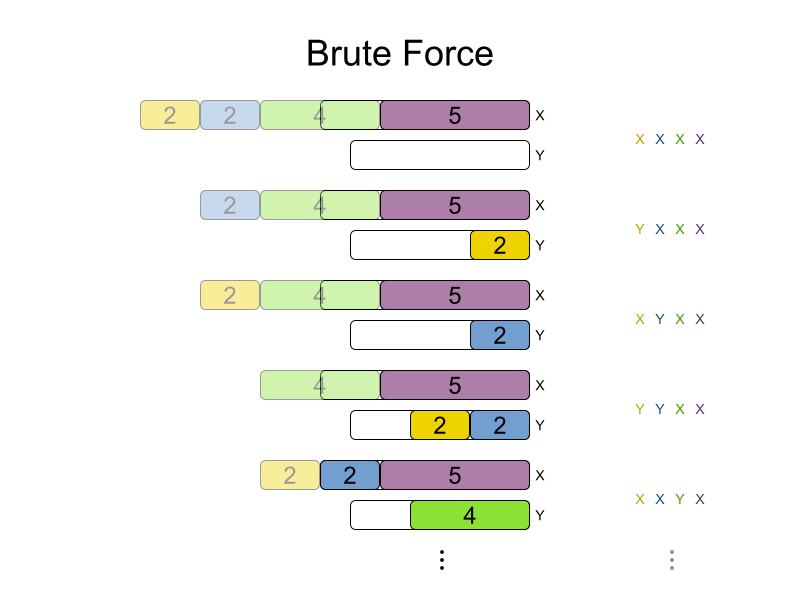
Brute Force config
<solver>
...
<exhaustiveSearch>
<exhaustiveSearchType>BRUTE_FORCE</exhaustiveSearchType>
</exhaustiveSearch>
</solver>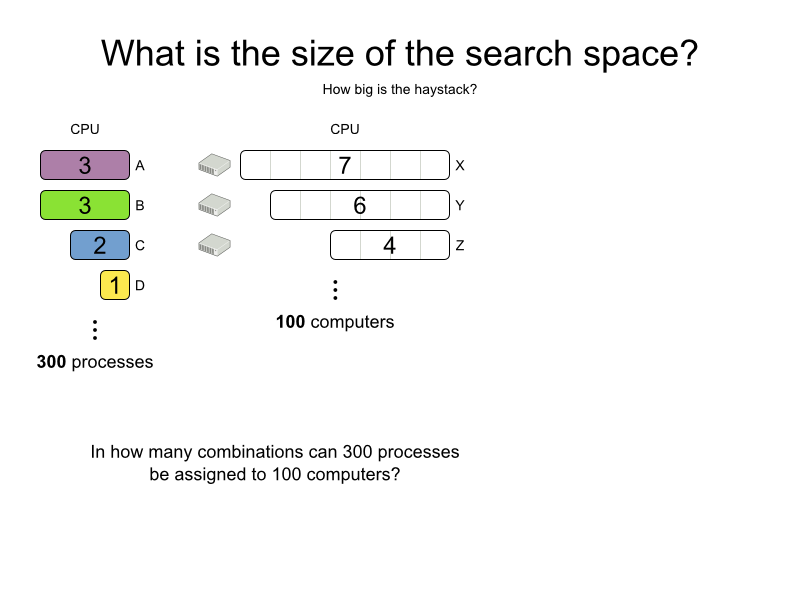
Brute Force scalability
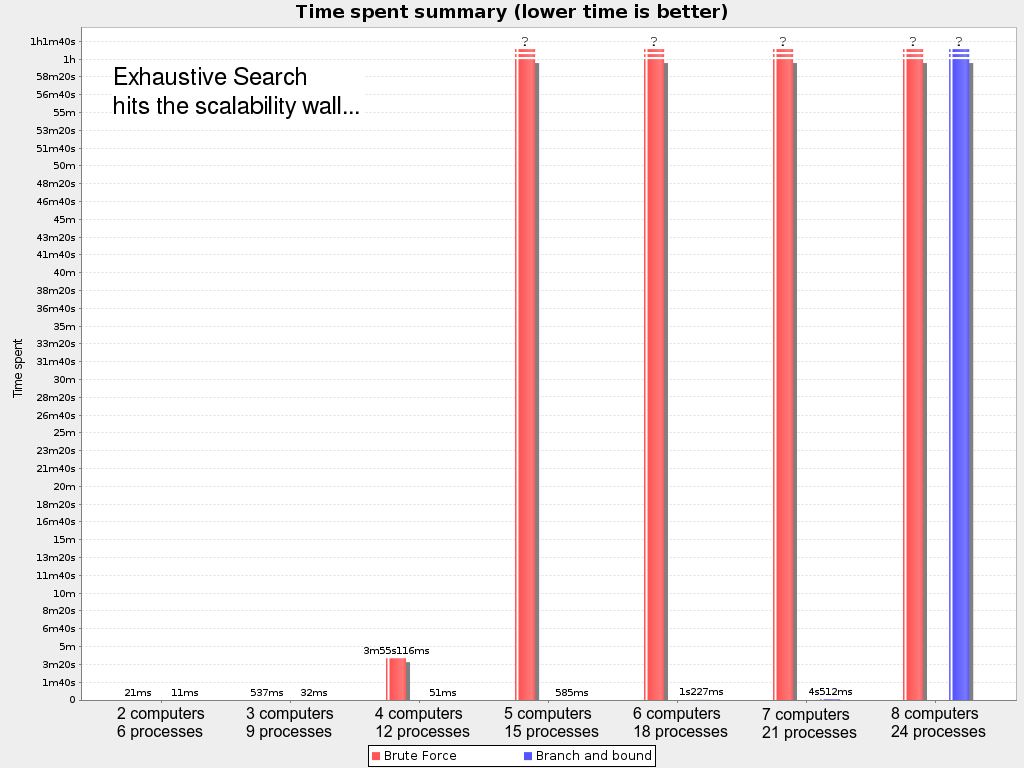
Plan 1200 processes
with Brute Force?
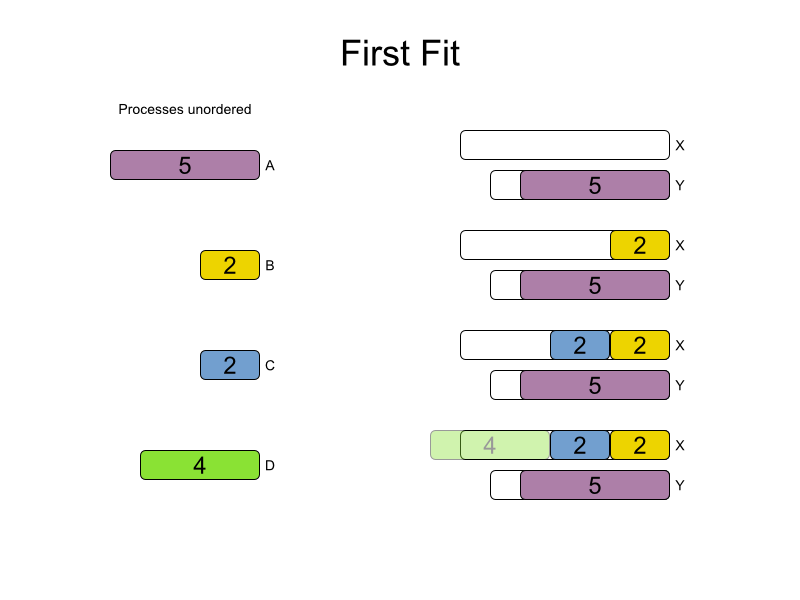
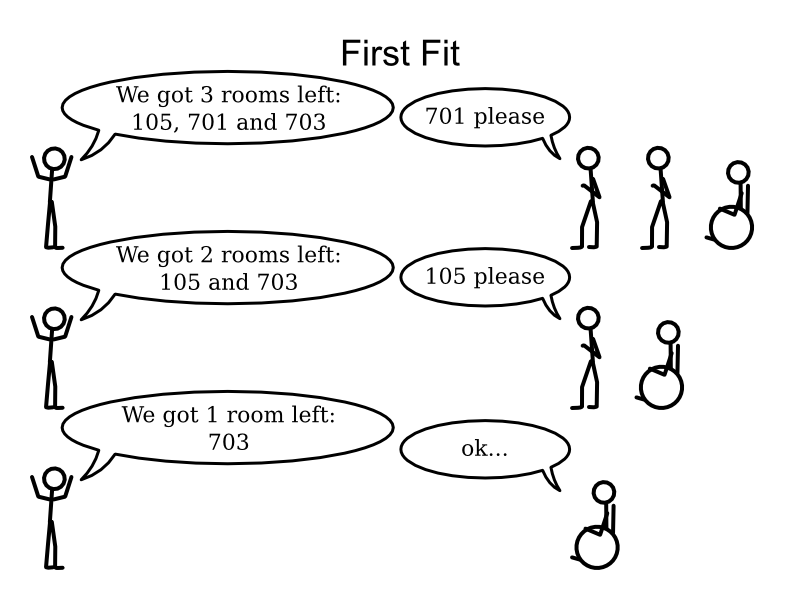
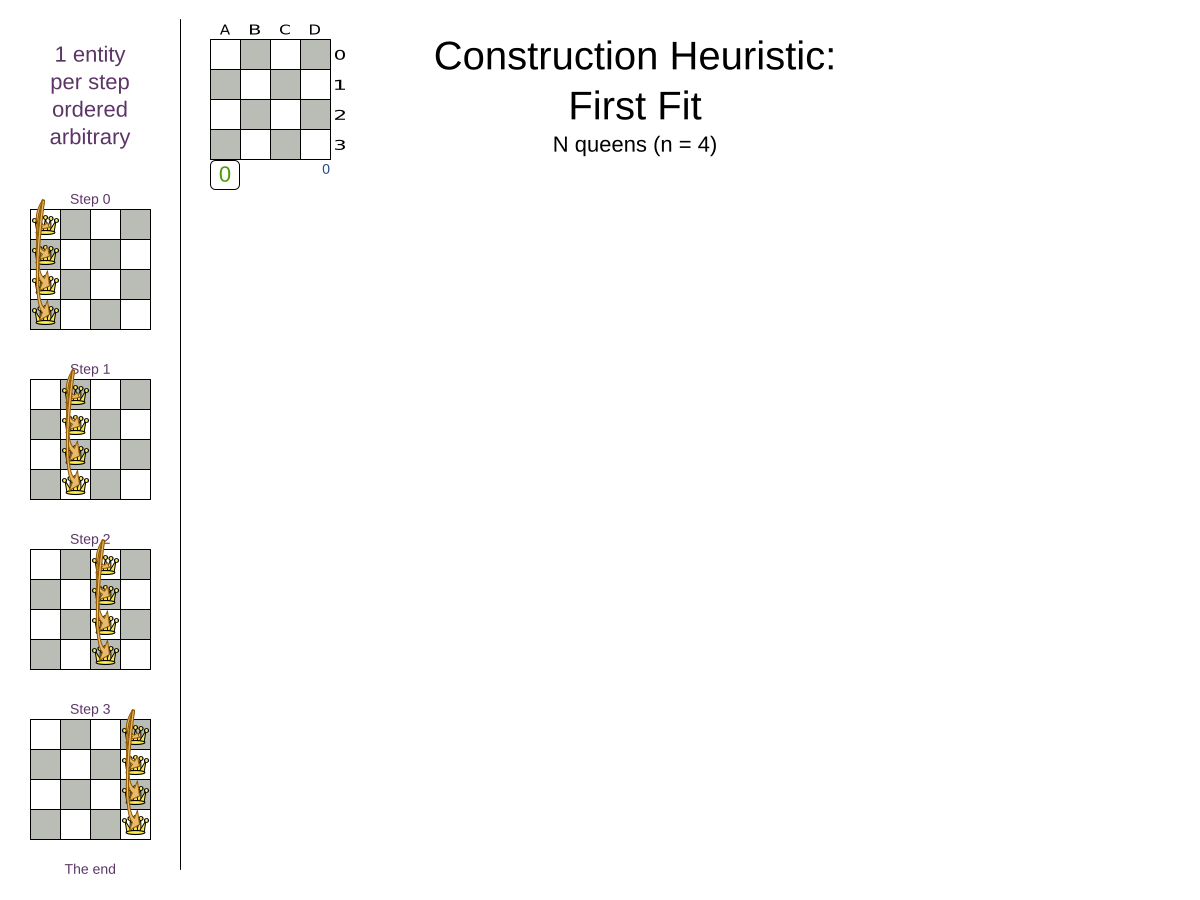
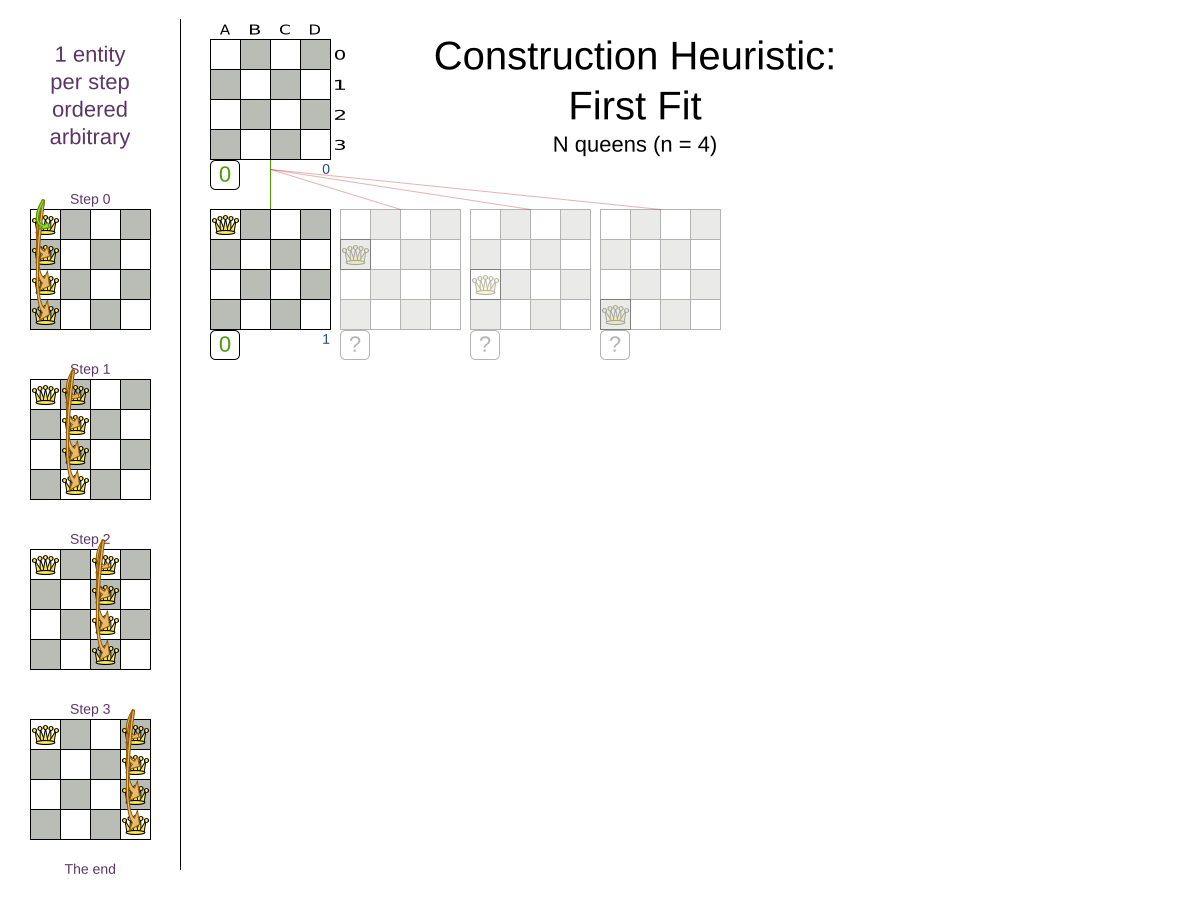
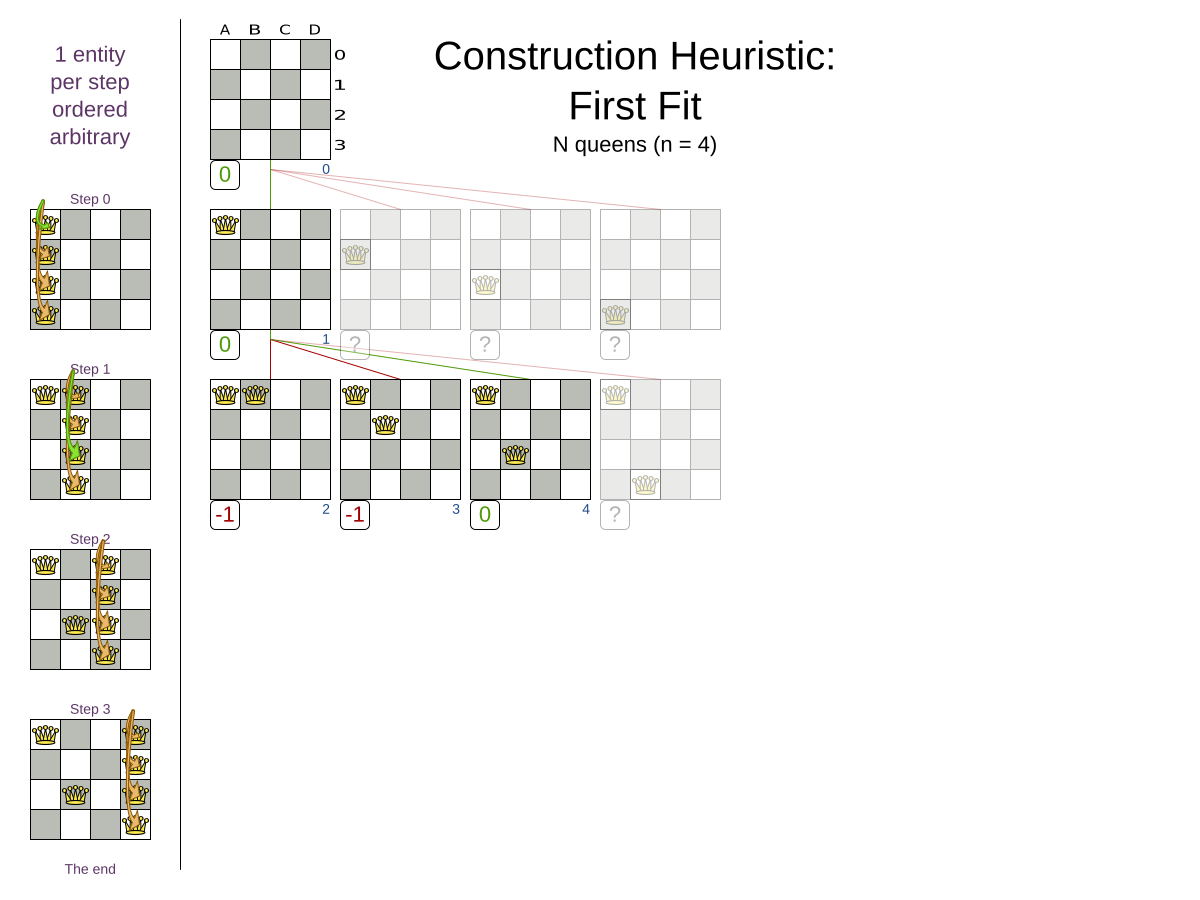
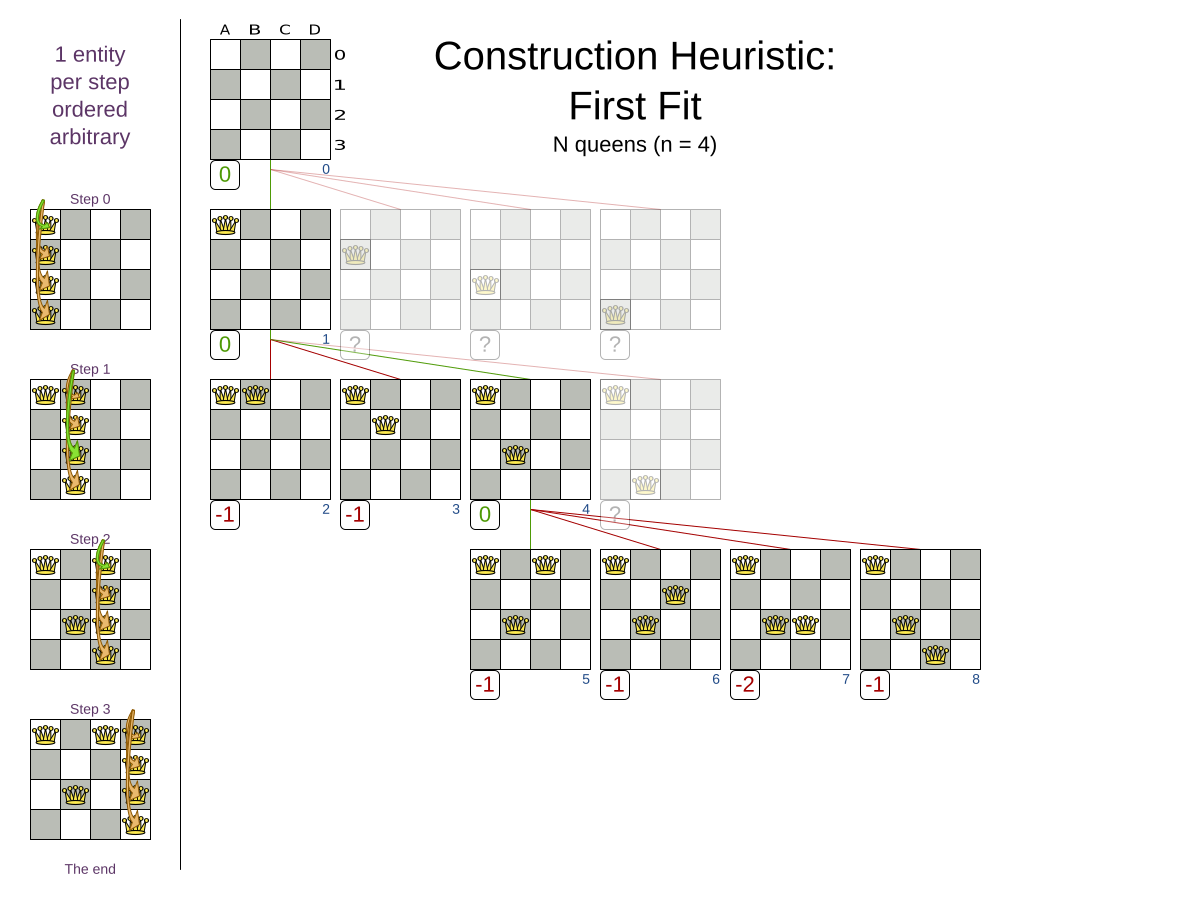
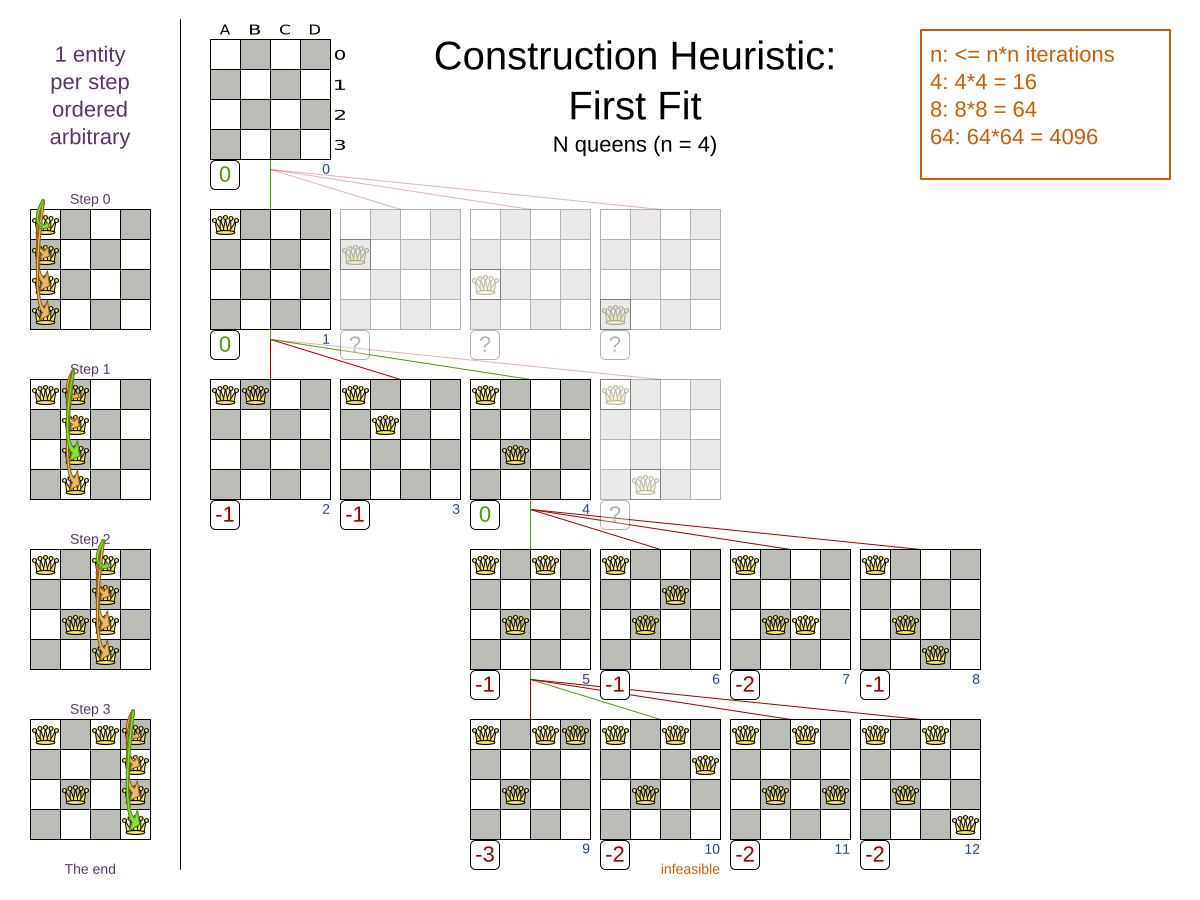
First Fit config
<solver>
...
<constructionHeuristic>
<constructionHeuristicType>FIRST_FIT</constructionHeuristicType>
</constructionHeuristic>
</solver>First Fit scalability
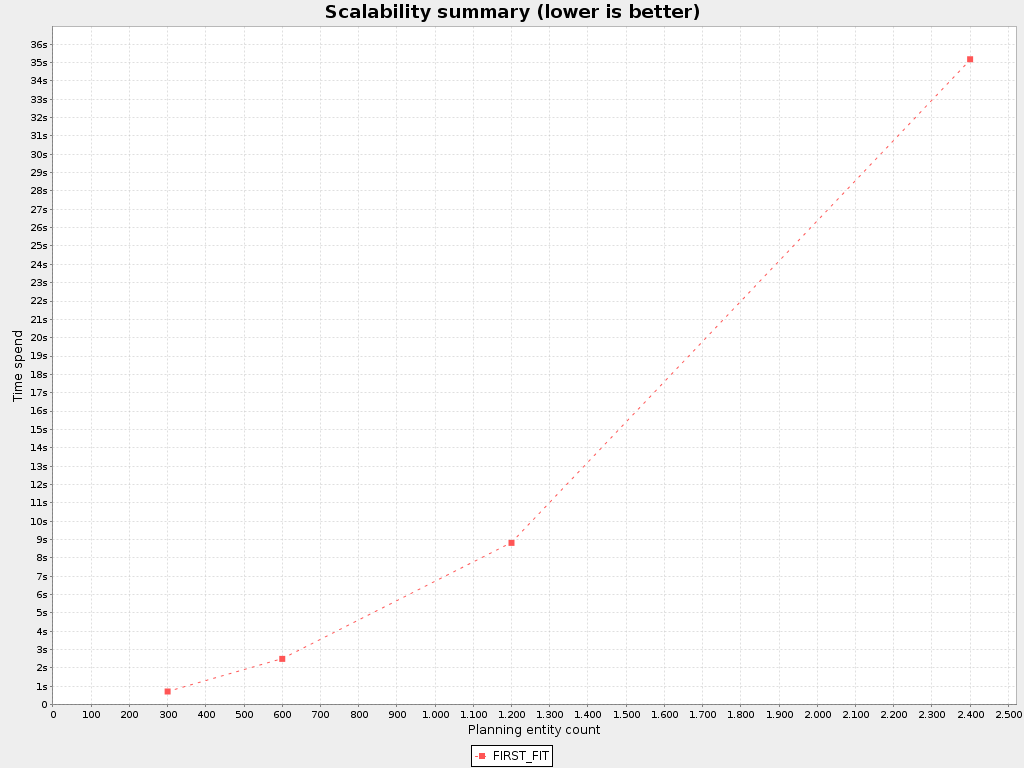
First Fit results
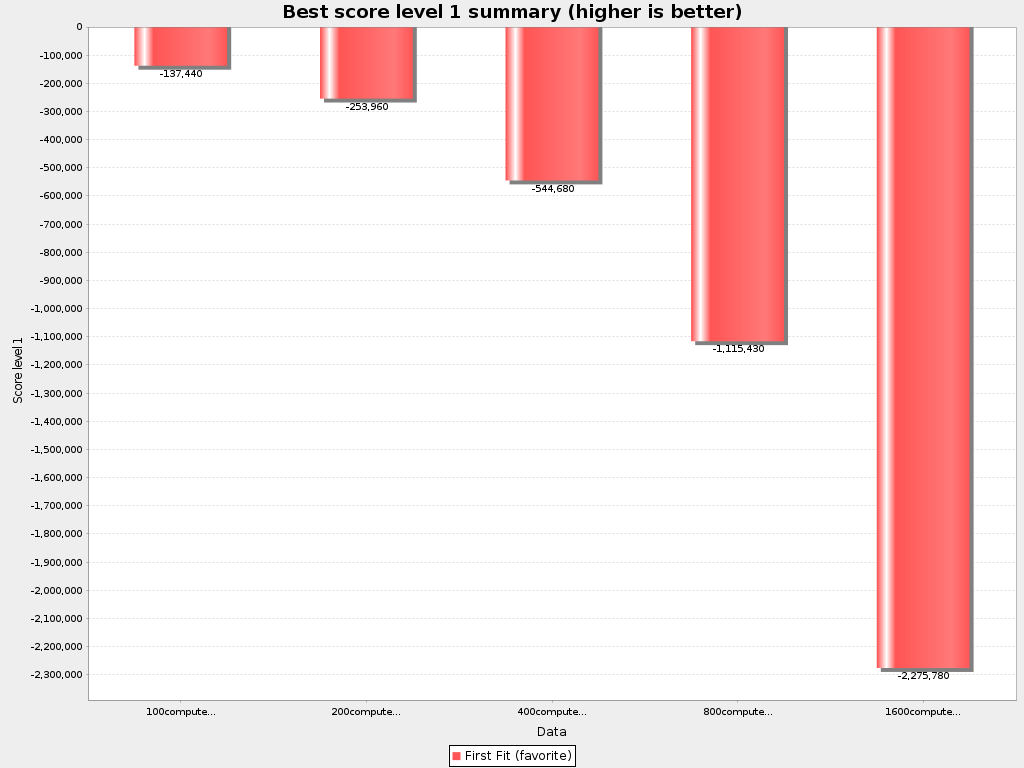
All hard constraints satisfied: maintenance cost shown
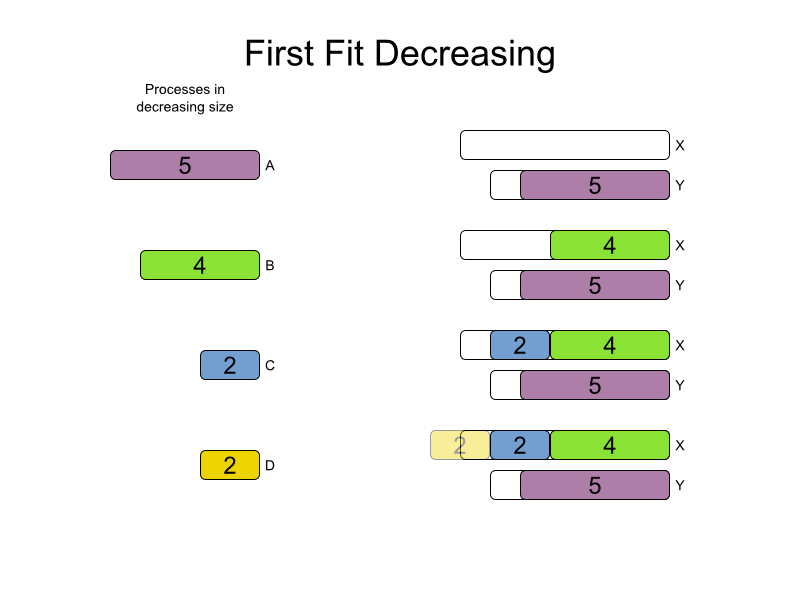
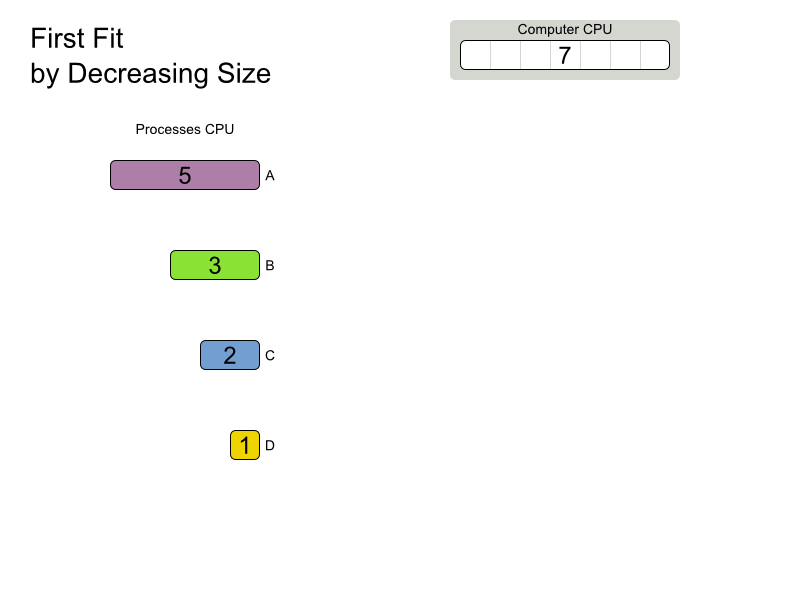
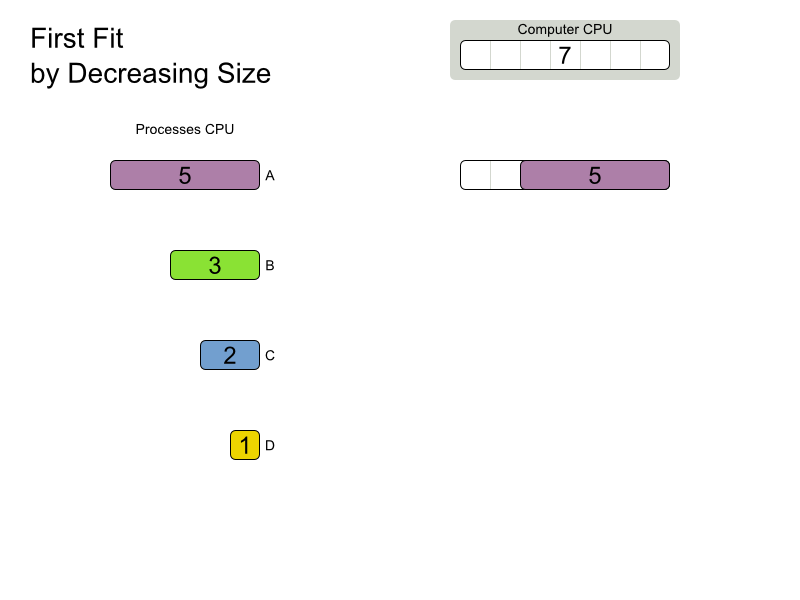
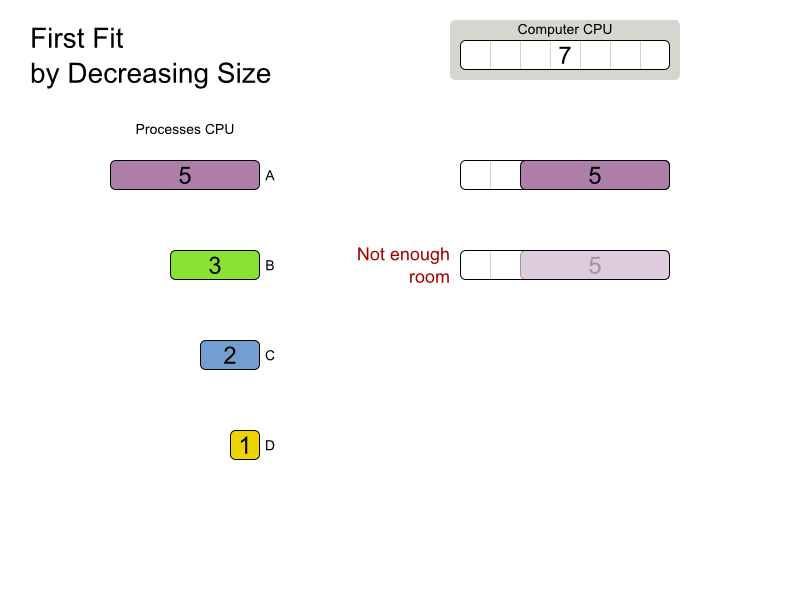
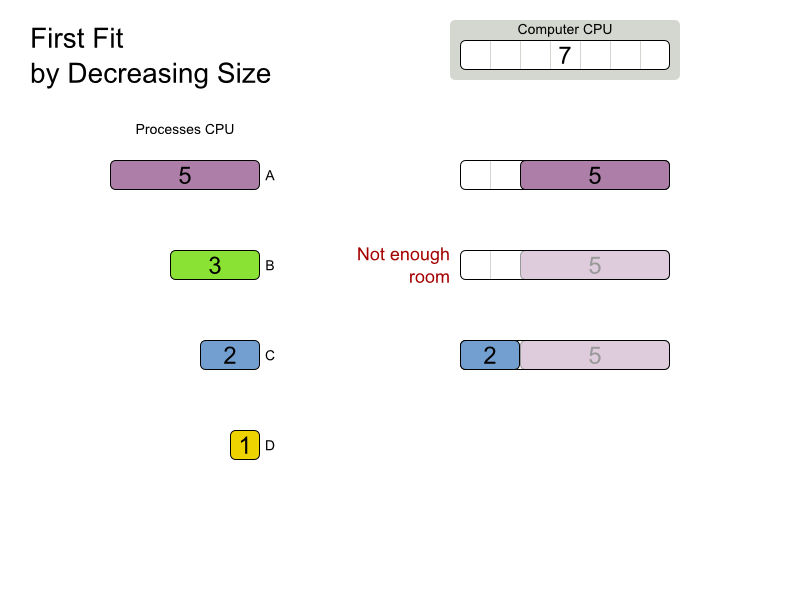
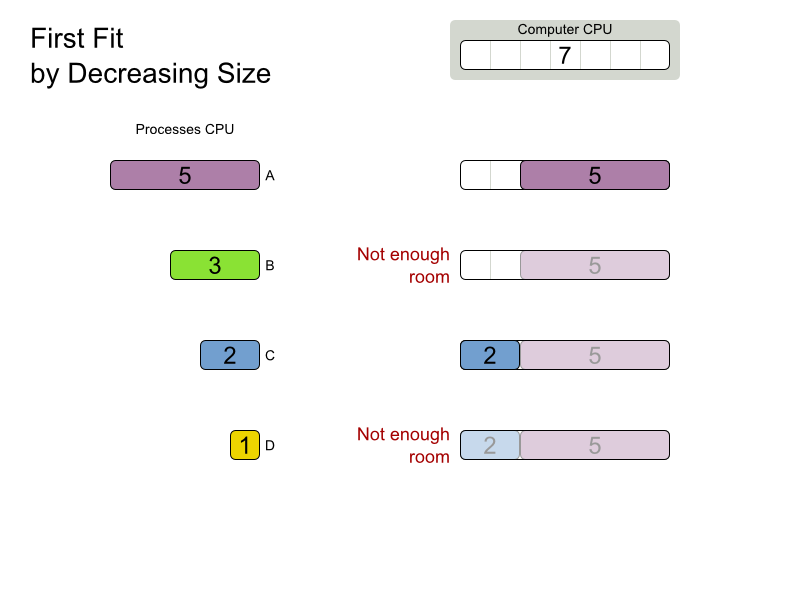
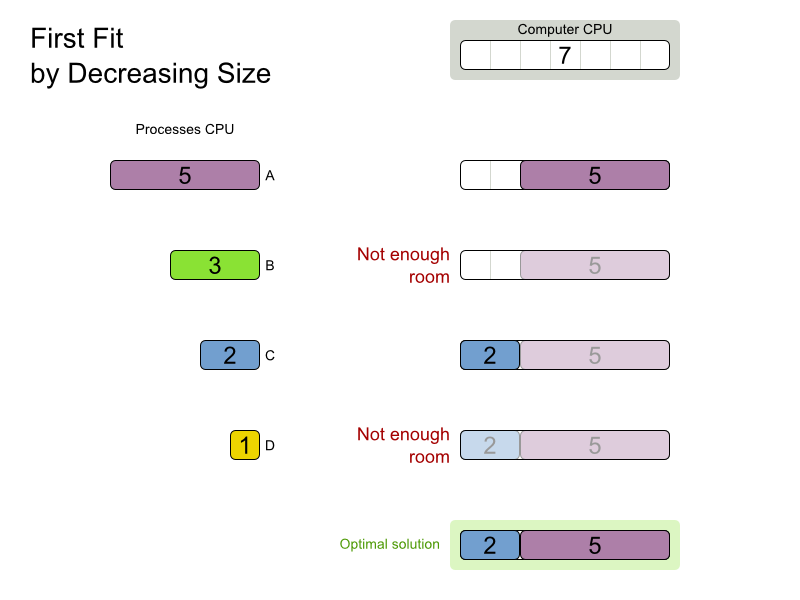
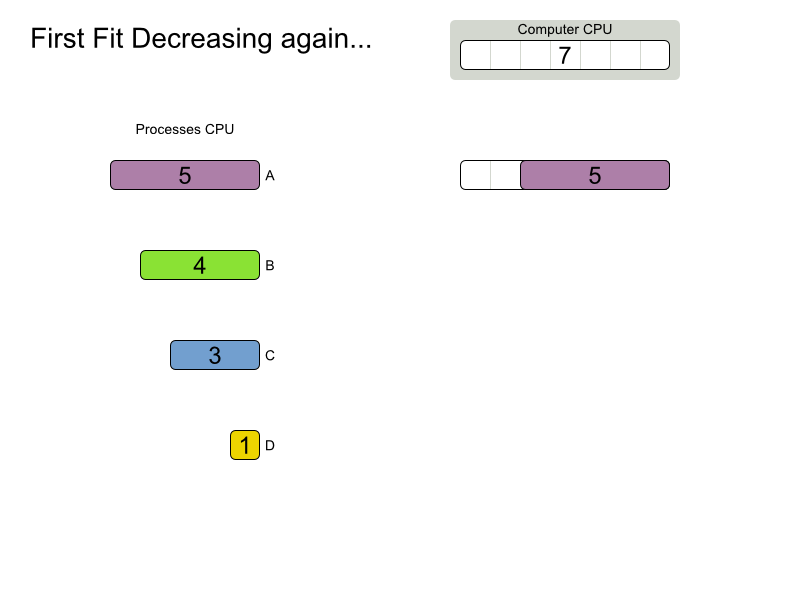
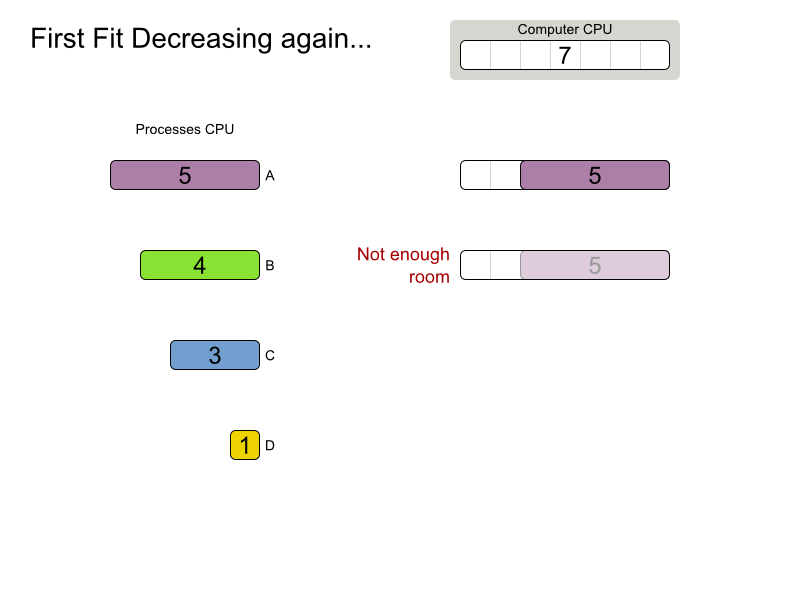
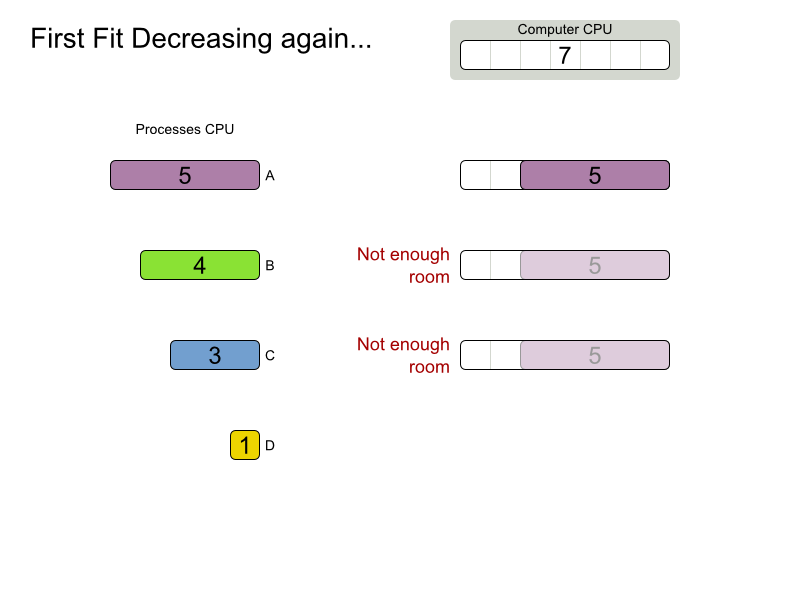
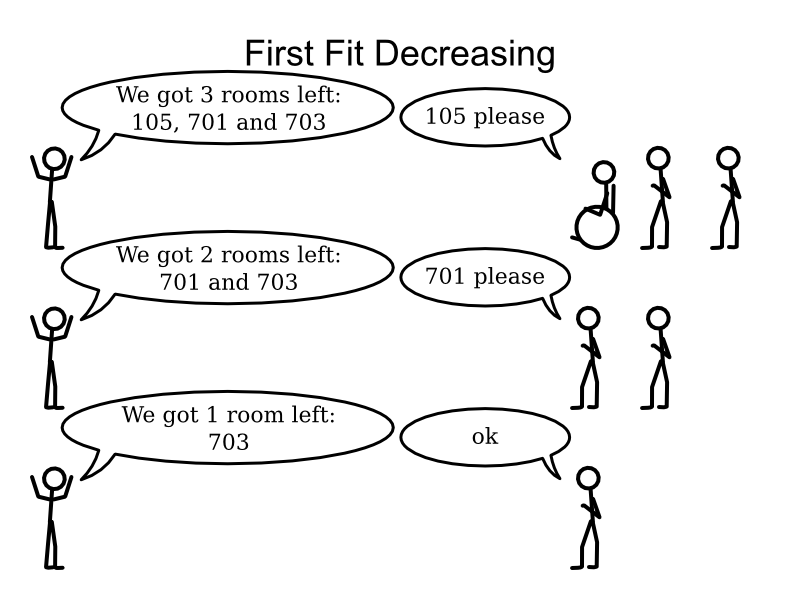
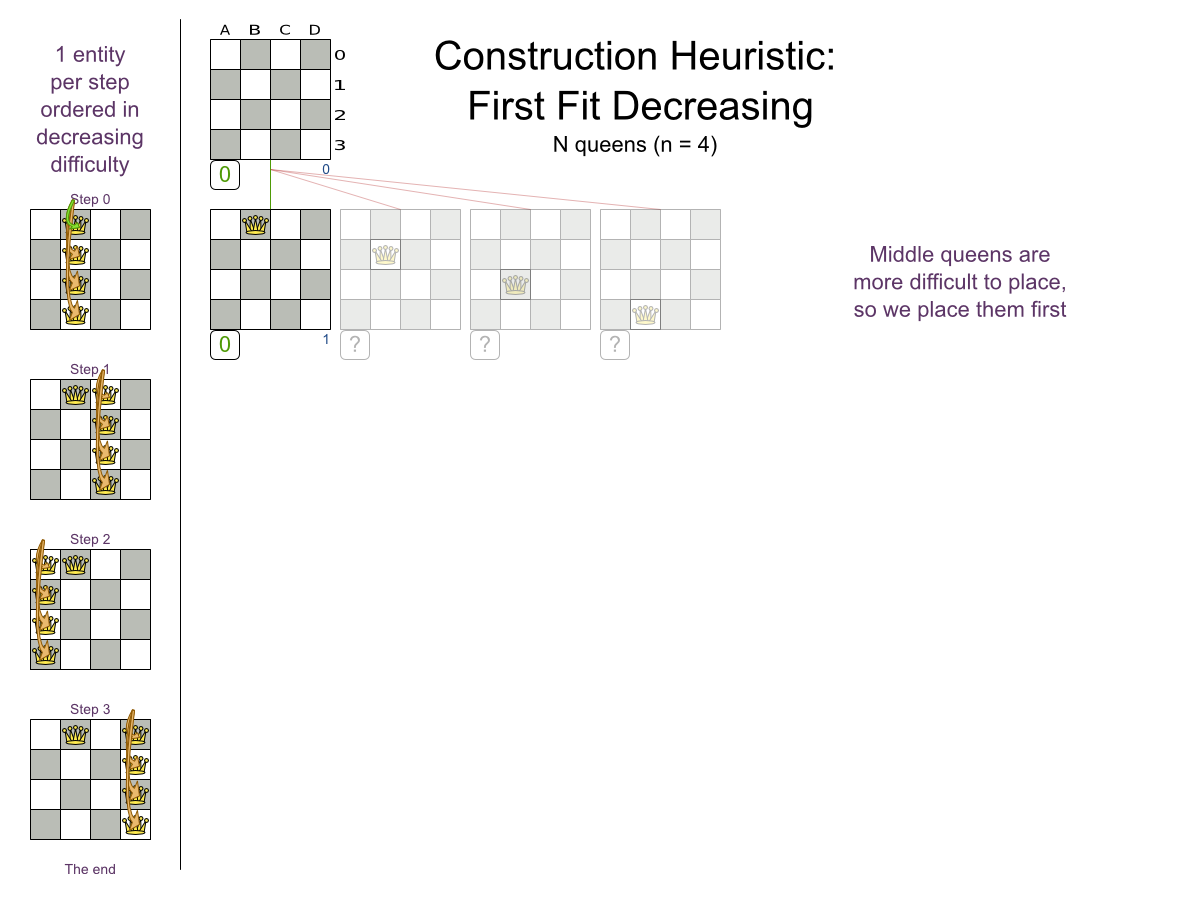
First Fit Decreasing config
<solver>
...
<constructionHeuristic>
<constructionHeuristicType>FIRST_FIT_DECREASING</constructionHeuristicType>
</constructionHeuristic>
</solver>DifficultyComparator
public class ProcessDifficultyComparator
implements Comparator<Process> {
public int compare(Process a, Process b) {
// Compare on requiredCpuPower * requiredMemory
// * requiredNetworkBandwidth
}
}
@PlanningEntity(difficultyComparatorClass
= ProcessDifficultyComparator.class)
public class Process {
...
}First Fit Decreasing scalability
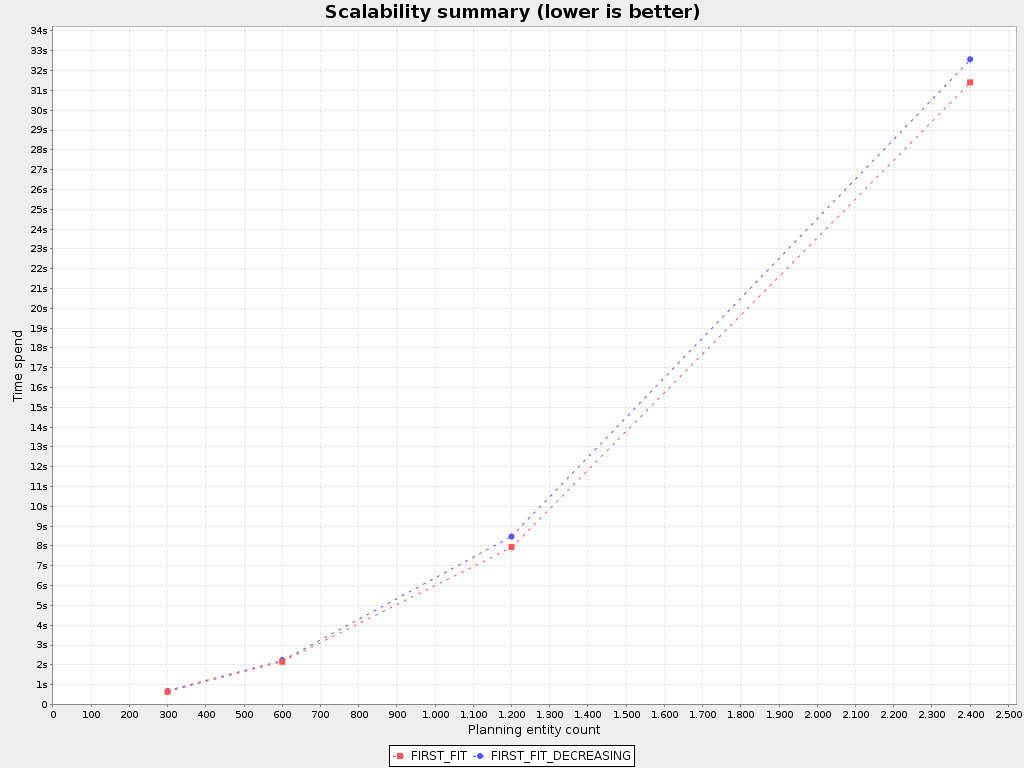
First Fit Decreasing results
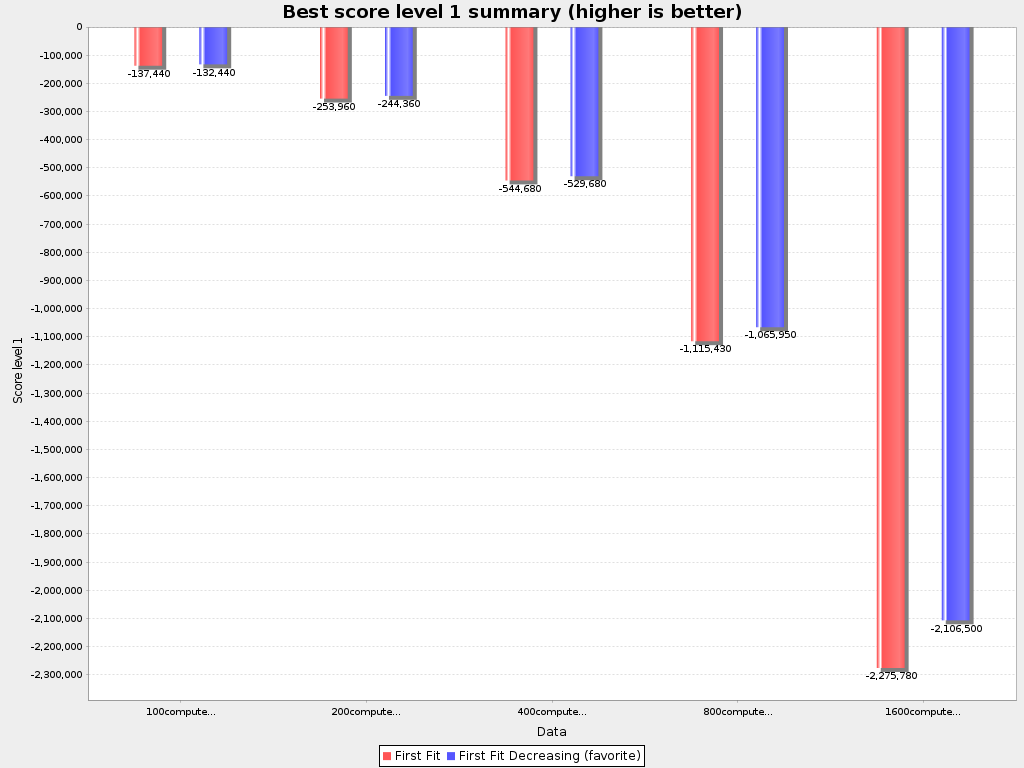
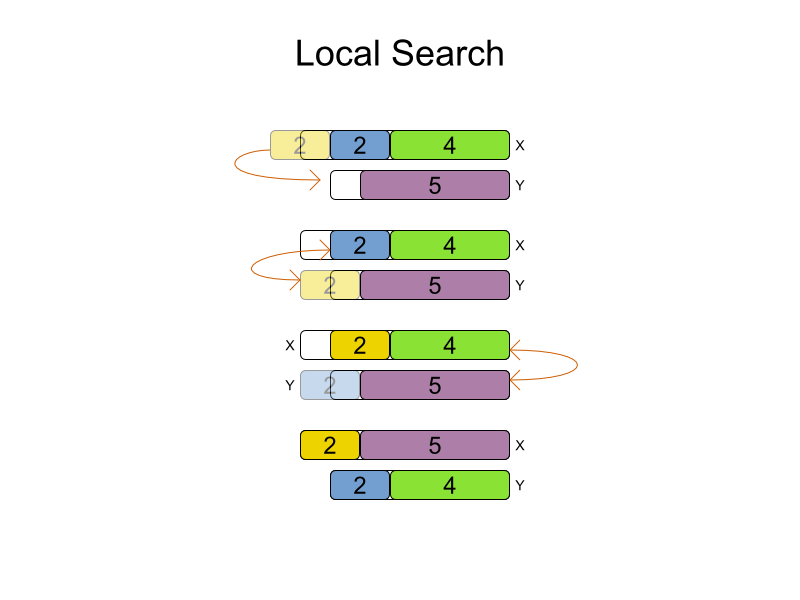
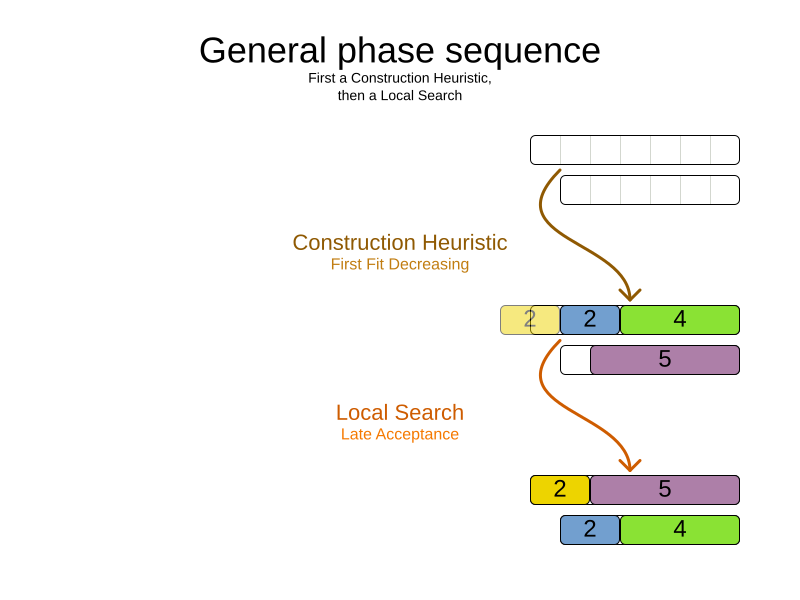
Construction Heuristics + Local Search
<solver>
...
<constructionHeuristic>
<constructionHeuristicType>FIRST_FIT_DECREASING</constructionHeuristicType>
</constructionHeuristic>
<localSearch>
...
<localSearch>
</solver>
Hill Climbing config
<localSearch>
<forager>
<!-- Untweaked standard value -->
<acceptedCountLimit>1000</acceptedCountLimit>
</forager>
</localSearch>
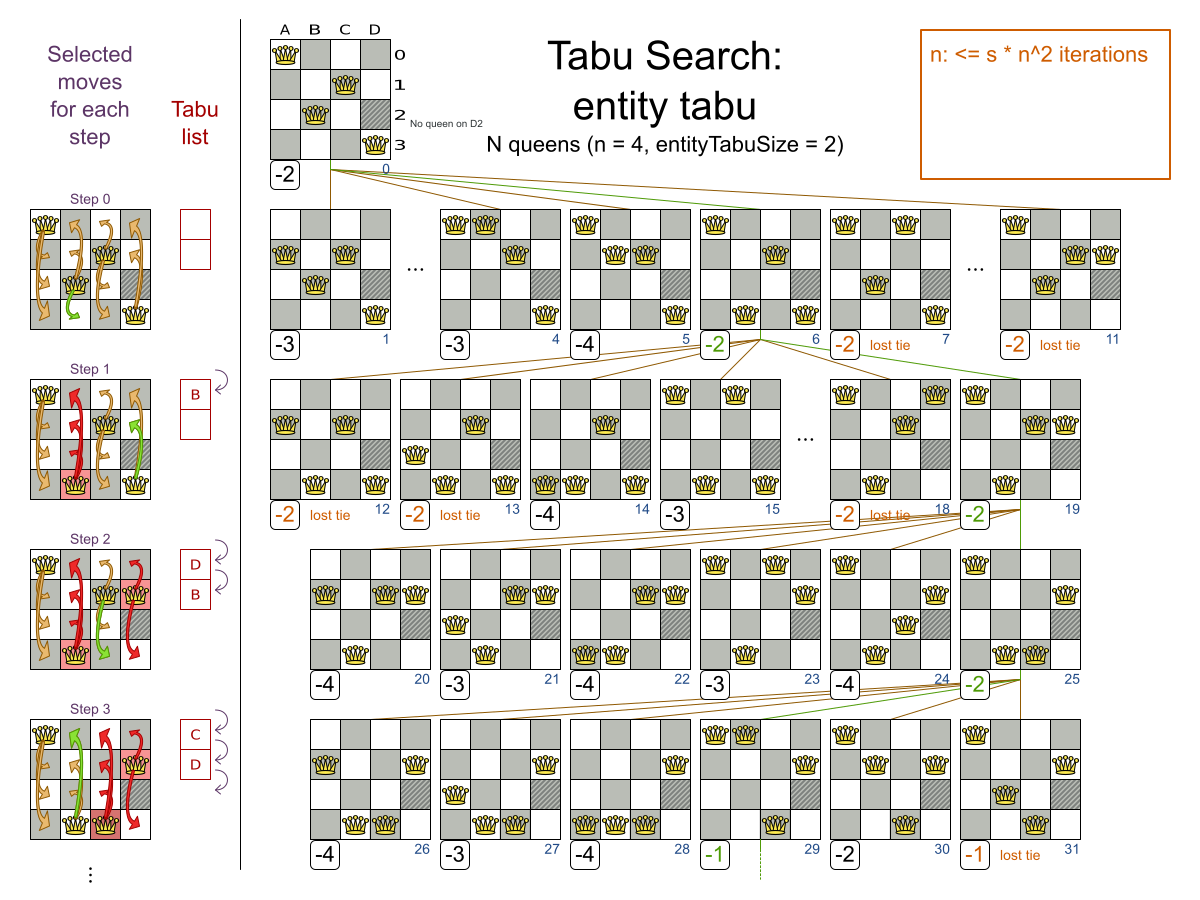
Tabu Search config
<localSearch>
<acceptor>
<!-- Typical standard value -->
<entityTabuSize>7</entityTabuSize>
</acceptor>
<forager>
<!-- Typical value -->
<acceptedCountLimit>1000</acceptedCountLimit>
</forager>
</localSearch>
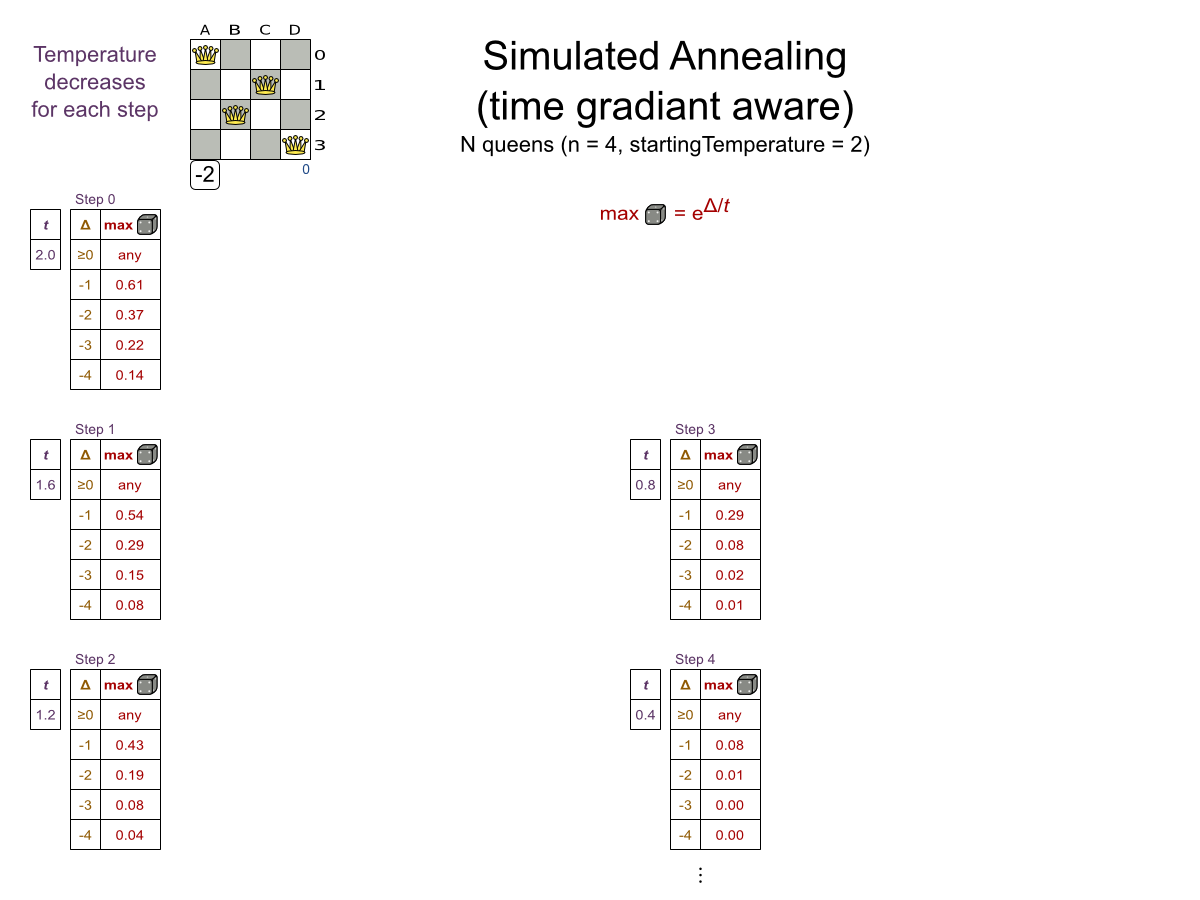
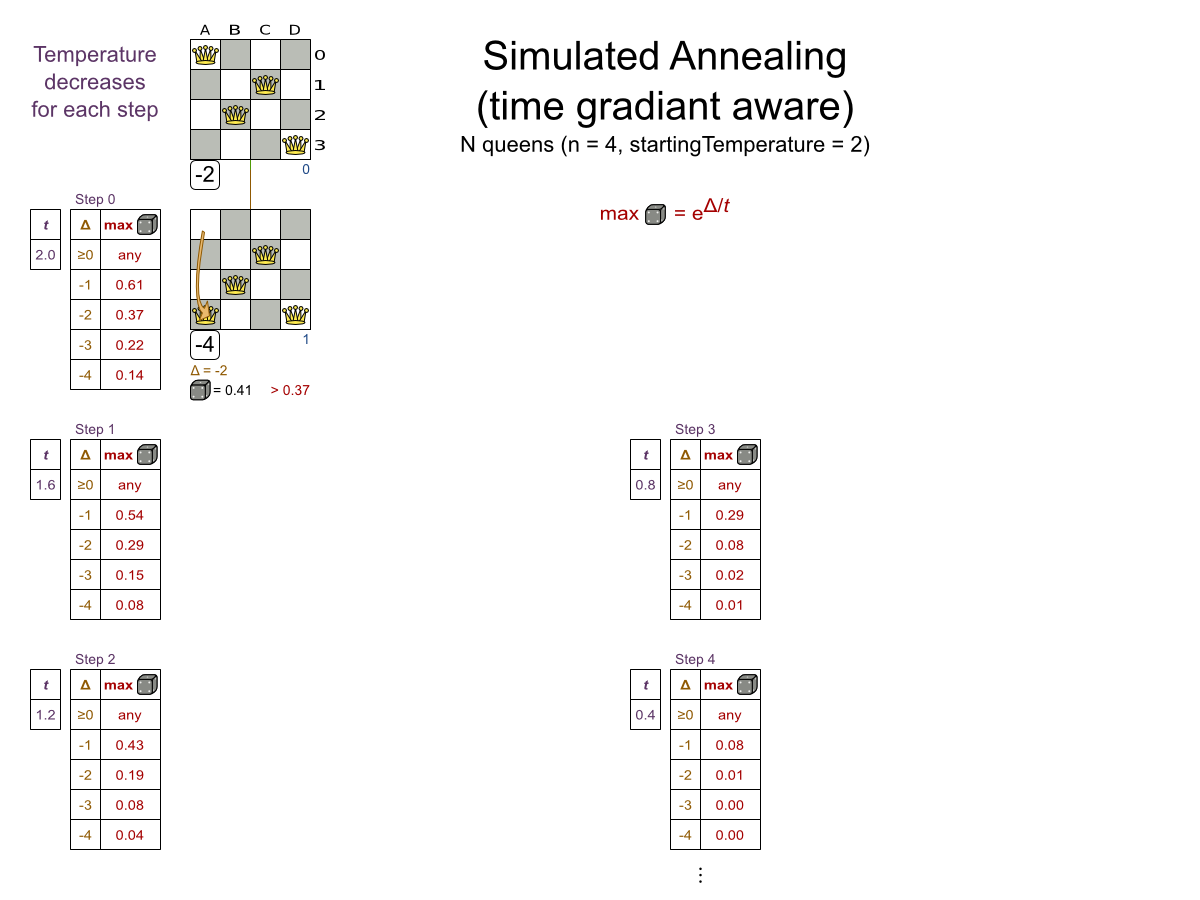
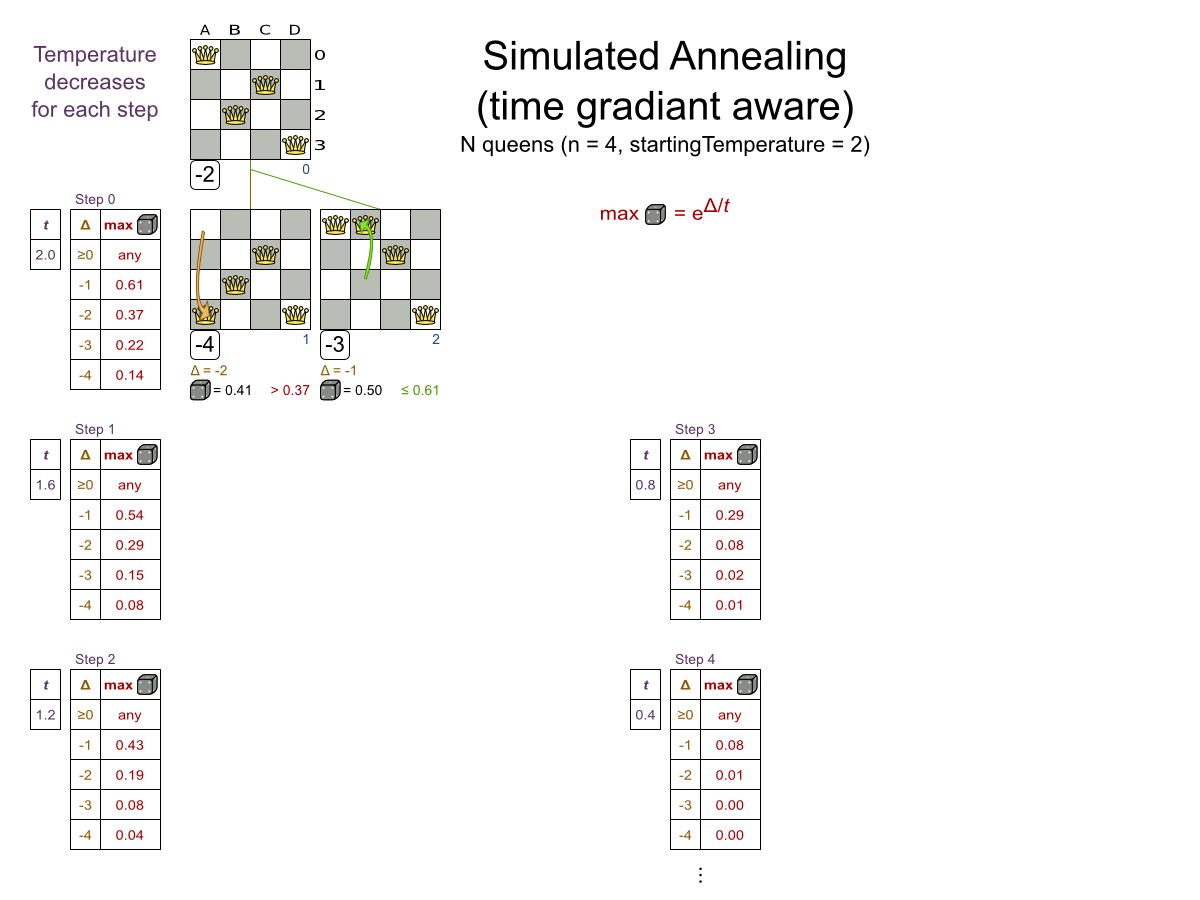
Simulated Annealing config
<localSearch>
<acceptor>
<!-- Tweaked value -->
<simulatedAnnealingStartingTemperature>
0hard/400soft
</simulatedAnnealingStartingTemperature>
</acceptor>
<forager>
<!-- Typical value -->
<acceptedCountLimit>4</acceptedCountLimit>
</forager>
</localSearch>
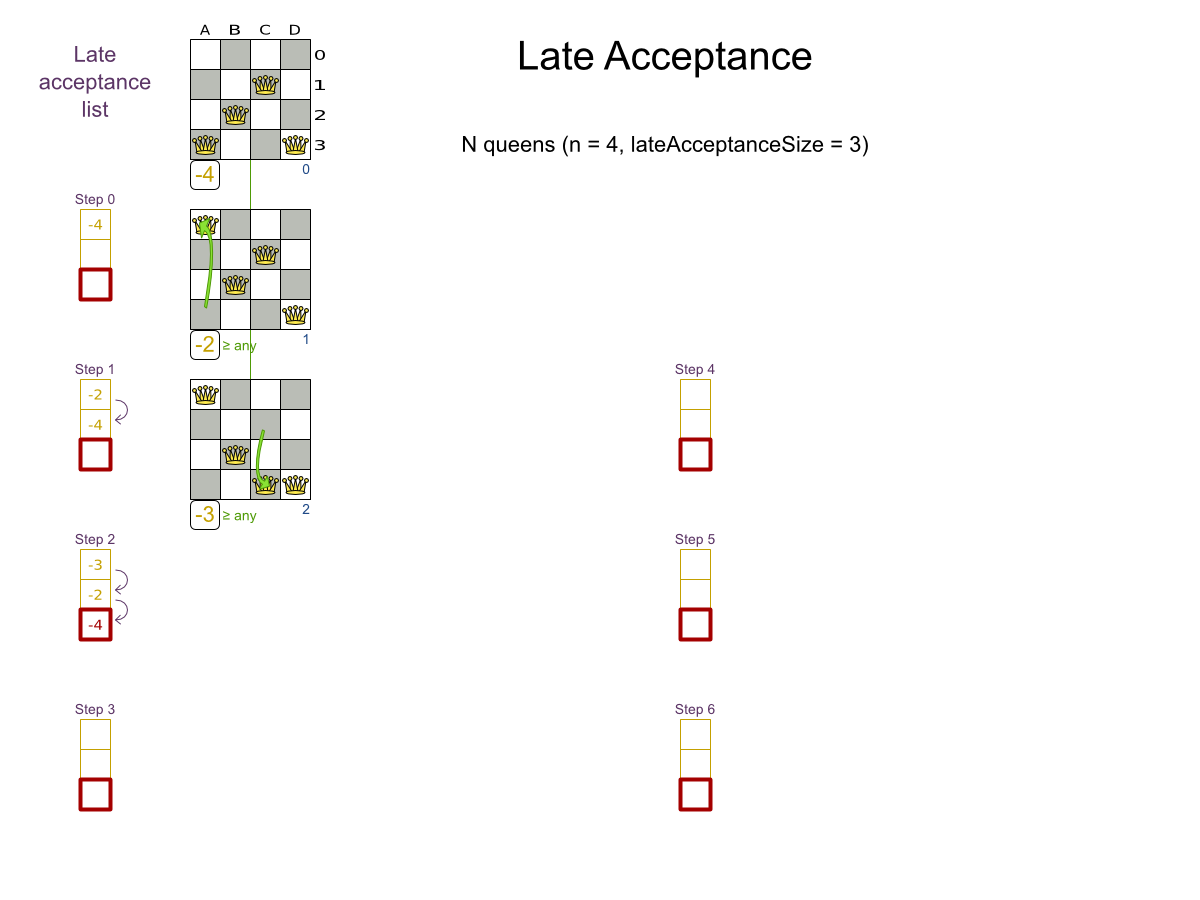
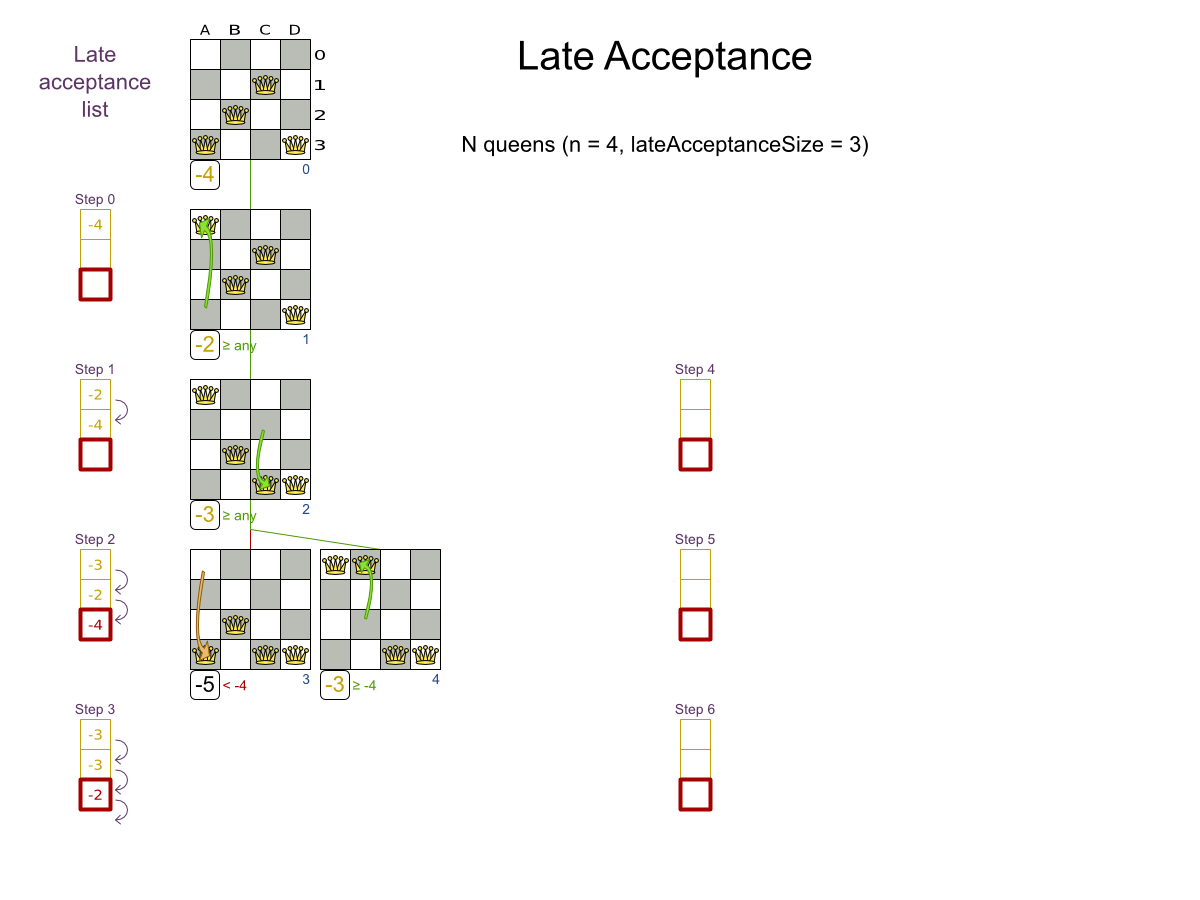
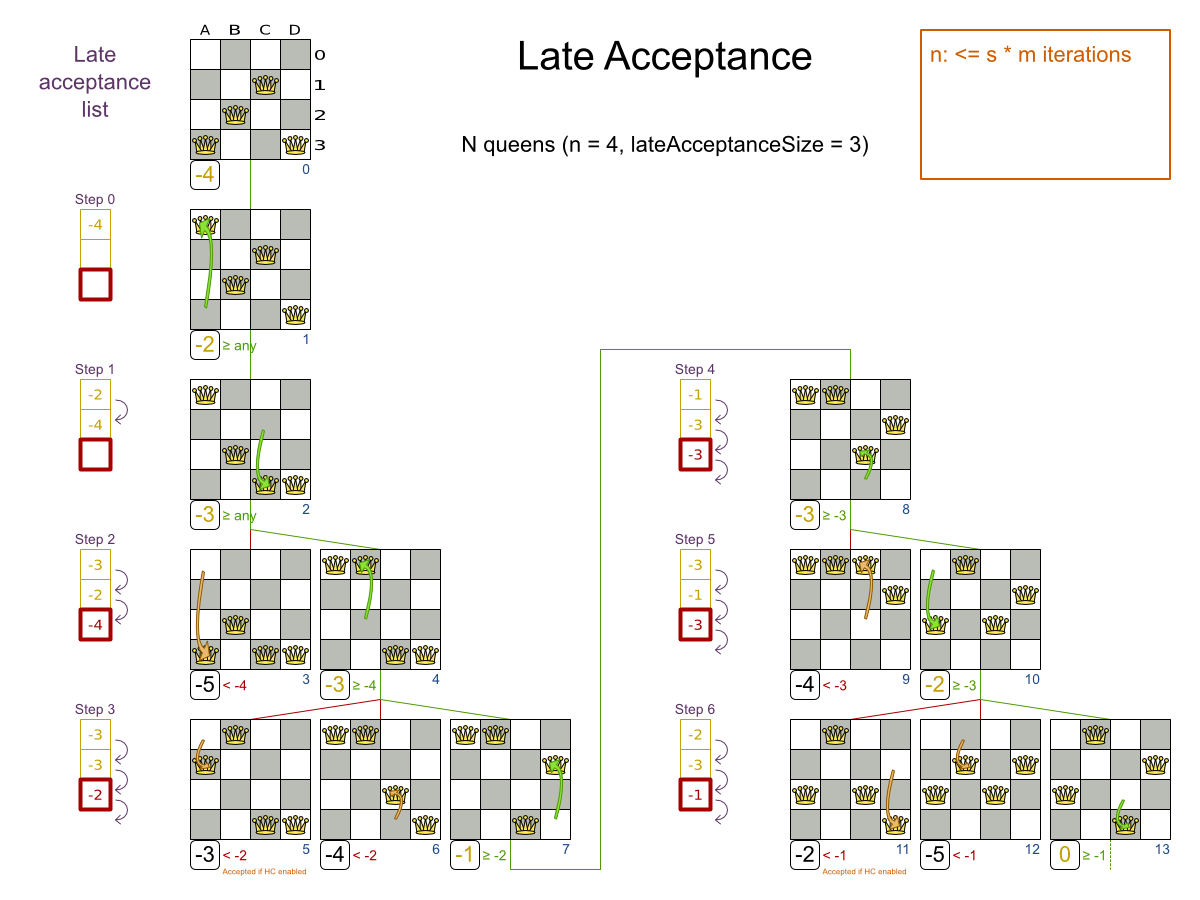
Late Acceptance config
<localSearch>
<acceptor>
<!-- Typical standard value -->
<lateAcceptanceSize>400</lateAcceptanceSize>
</acceptor>
<forager>
<!-- Typical value -->
<acceptedCountLimit>4</acceptedCountLimit>
</forager>
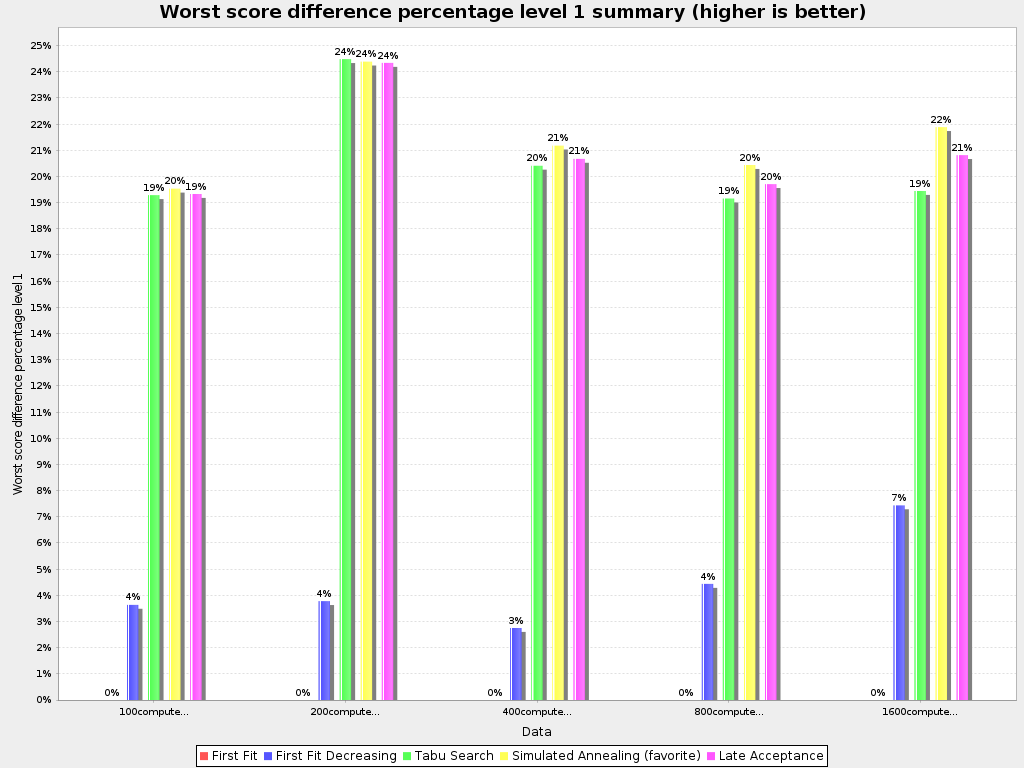
</localSearch>Local Search results
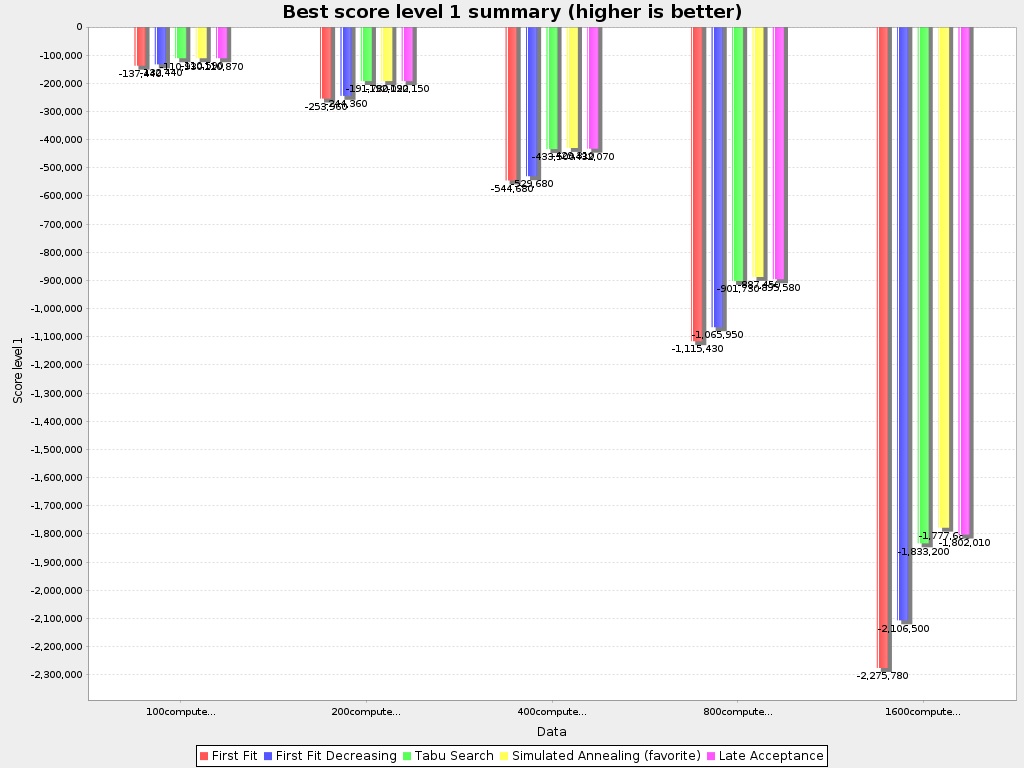
Cost ($) reduction
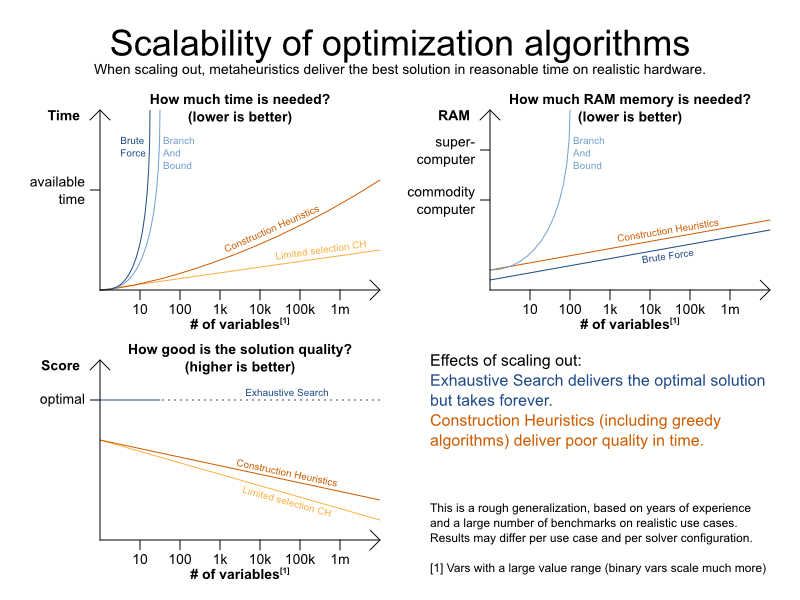
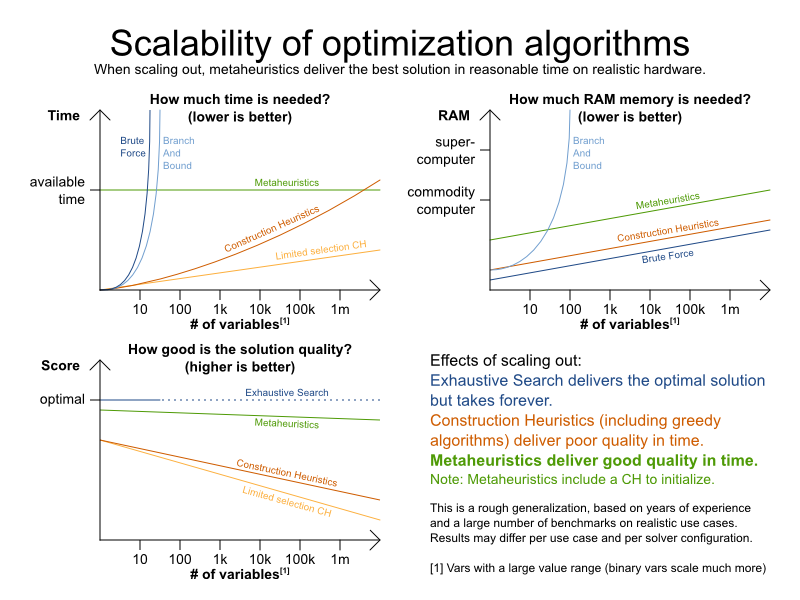
Optimization algorithms
-
Exhaustive Search
- Brute Force
- Branch And Bound
-
Construction Heuristics
- First Fit (Decreasing)
- Weakest/Strongest Fit (Decreasing)
- Cheapest Insertion
-
Metaheuristics (Local Search, ...)
- Hill Climbing
- Tabu Search
- Strategic Oscillation Tabu Search
- Simulated Annealing
- Late Acceptance
- Step Counting Hill Climbing
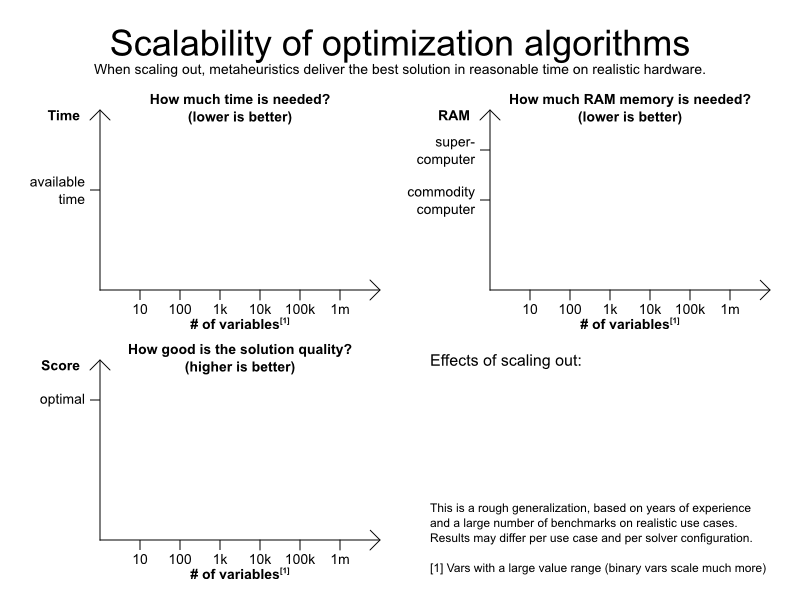
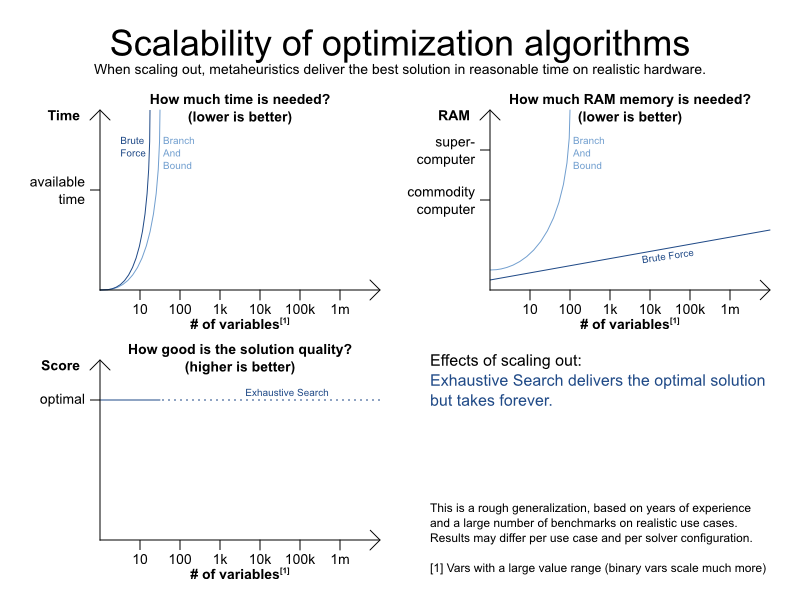
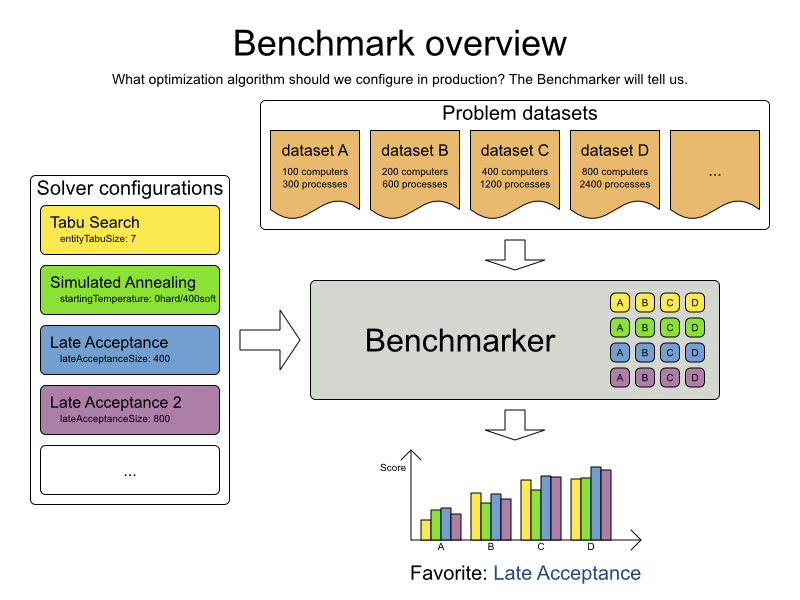
Benchmarker toolkit
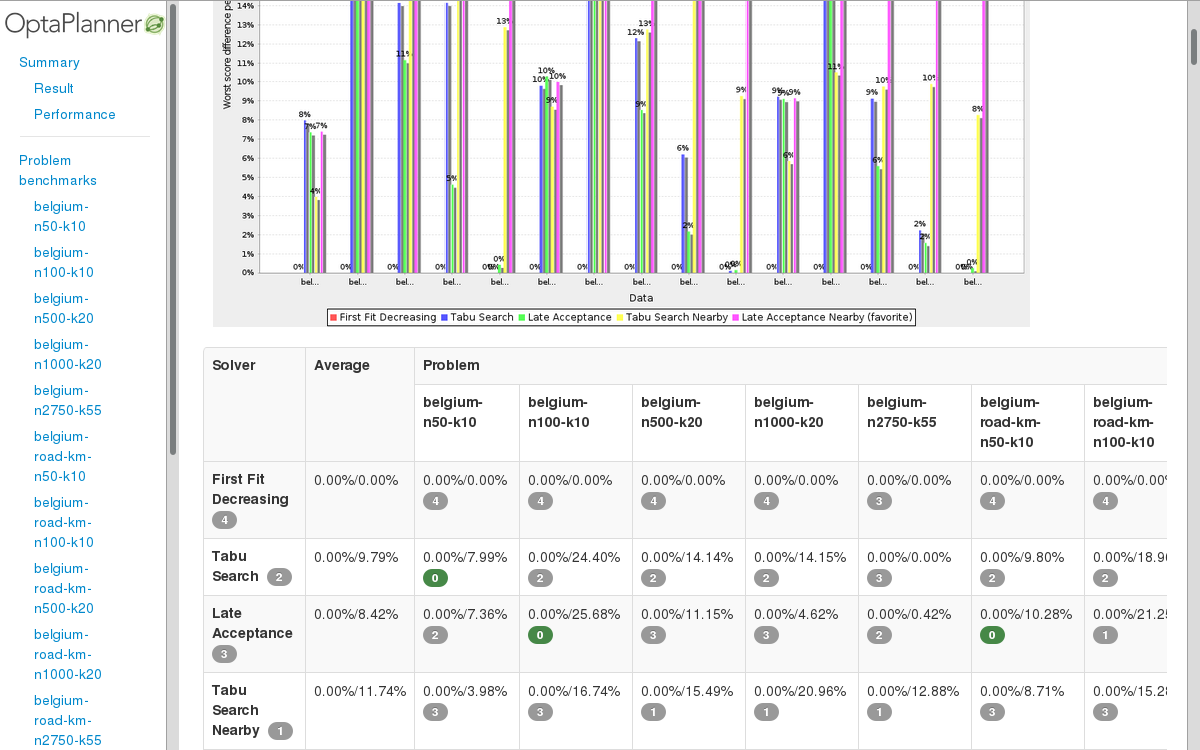
Benchmark report demo
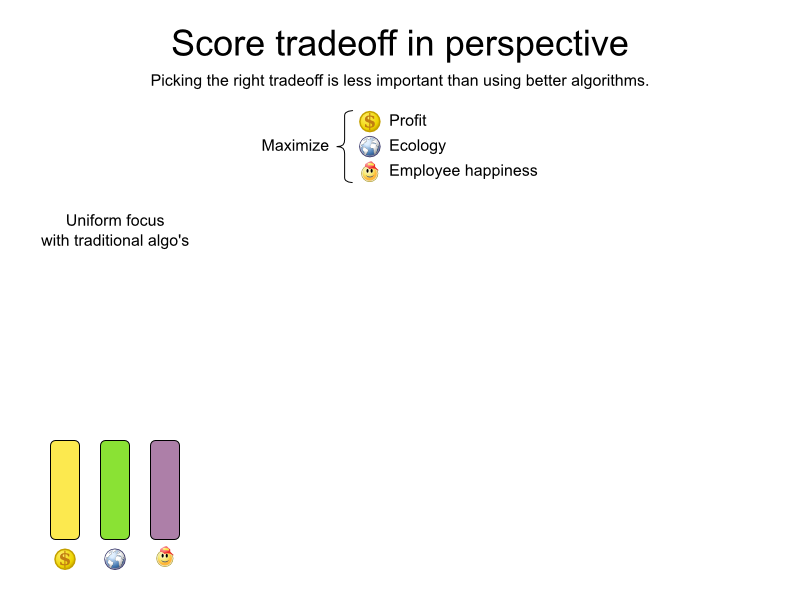
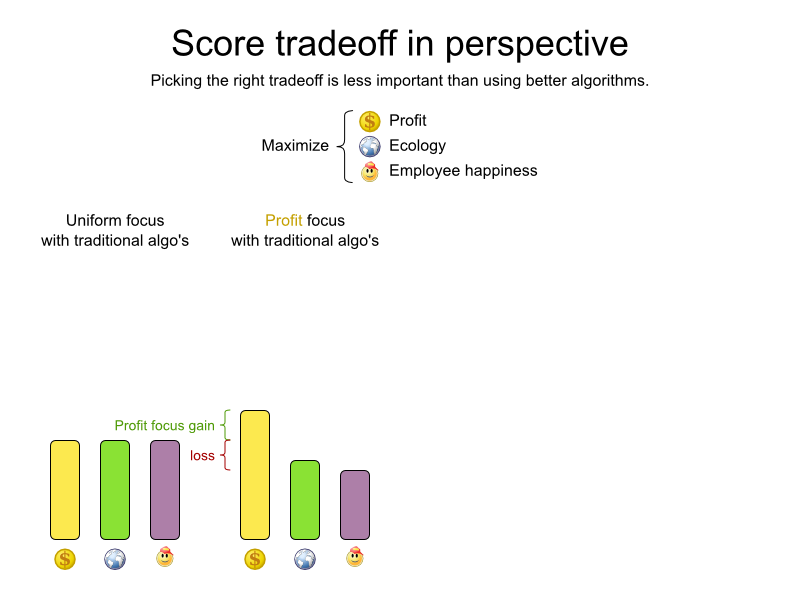
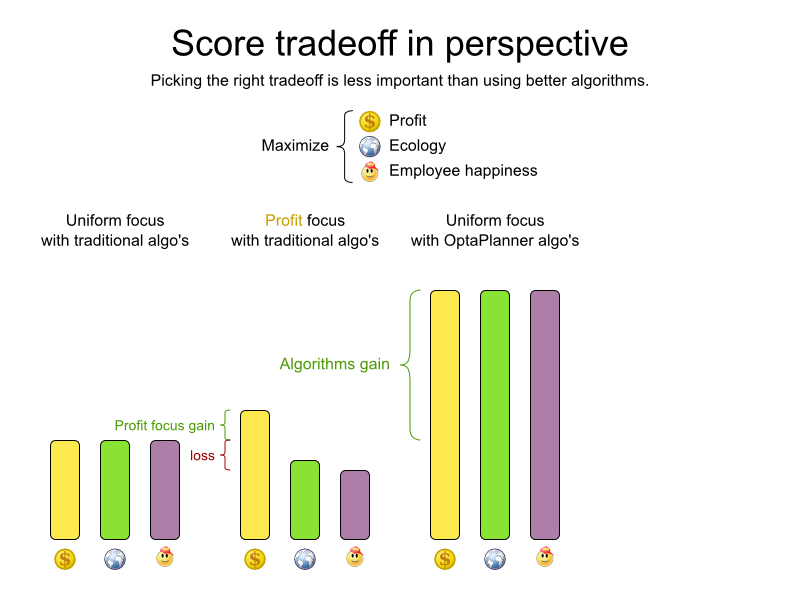
Gain by using OptaPlanner
| Use case | Gain type | Avg | Min | Max |
|---|---|---|---|---|
| Cloud Balancing | Maintenance cost 1 | -18% | -16% | -21% |
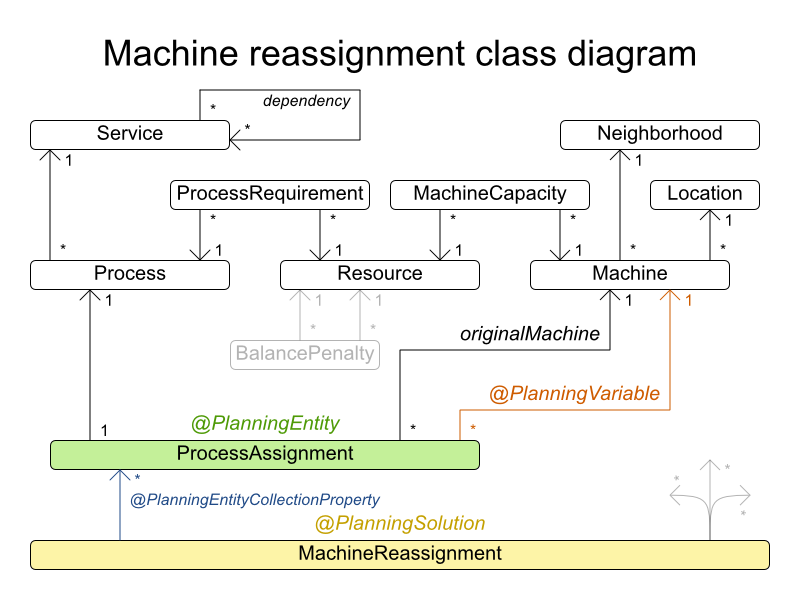
| Machine Reassignment | Unbalanced load 2 | -63% | -25% | -97% |
| Vehicle Routing (Belgium datasets) |
Distance 1 | -20% | -7% | -27% |
| Nurse rostering | Happiness 1 | +53% | -19% | -85% |
| Course scheduling | Unhappiness 1 | -66% | -26% | -100% |
OptaPlanner in a 5 minute run
1 Compared to traditional algorithms with domain knowledge.
2 Compared to initial assignments.
Optimization algorithms 101
Take the red pill
Press down to show
Press right to skip
N Queens demo

demo
Simplified problem
N Queens
- Place n queens on a n sized chessboard
- No 2 queens can attach each other
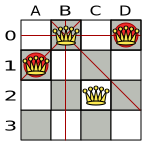
Bad
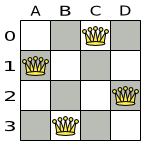
Good
- Imperfect example
- Not NP-complete (shortcuts exist)
- Score function is too simple (too black/white)
What solution is better?
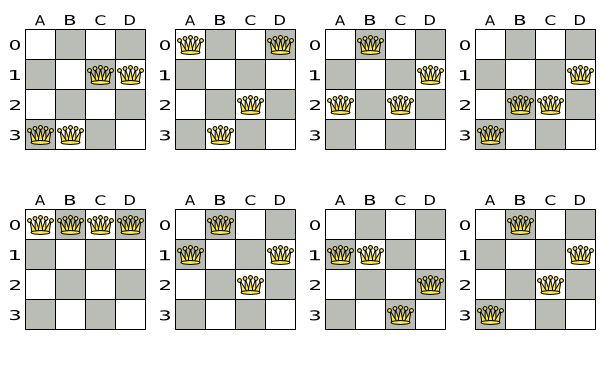
- Need for objective scoring
- Better score ⇔ better solution
- Highest score ⇔ optimal solution


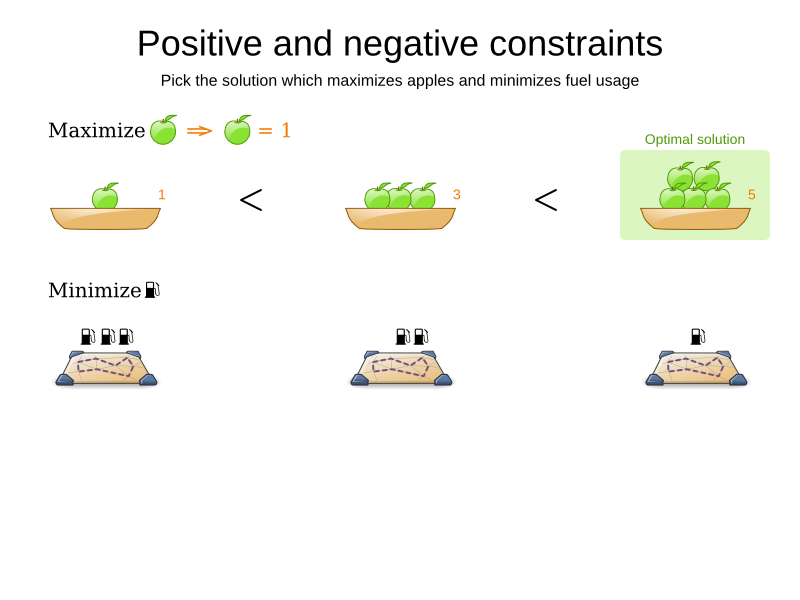

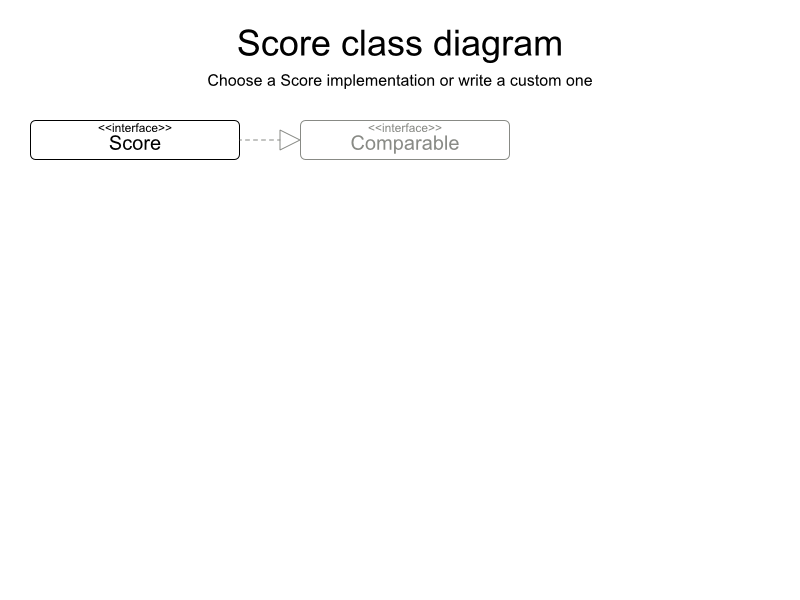
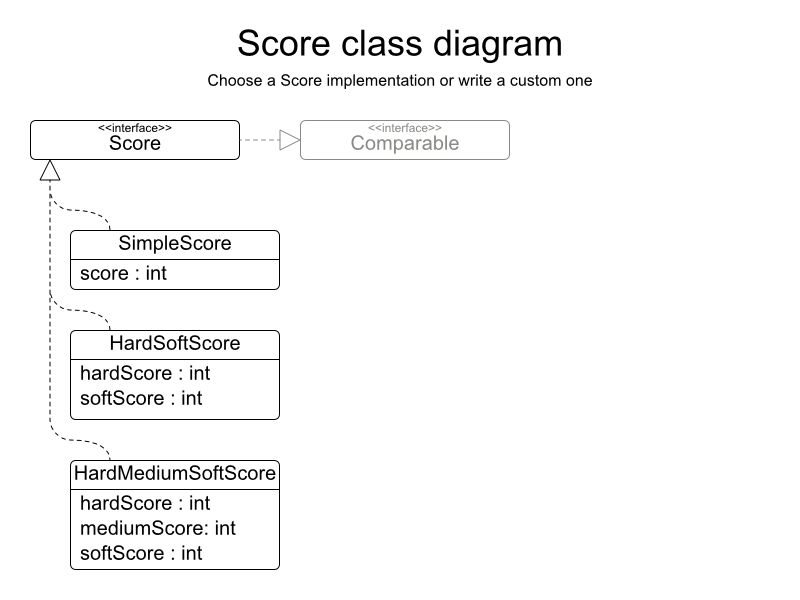
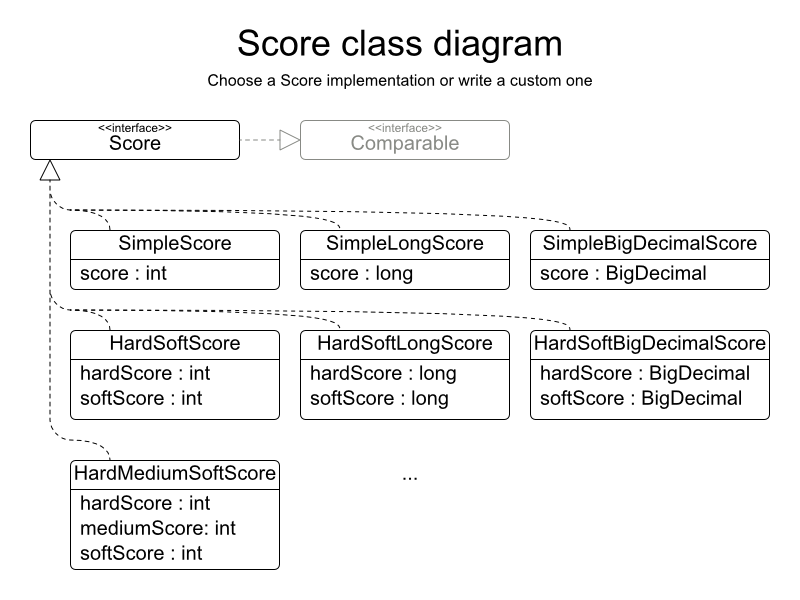
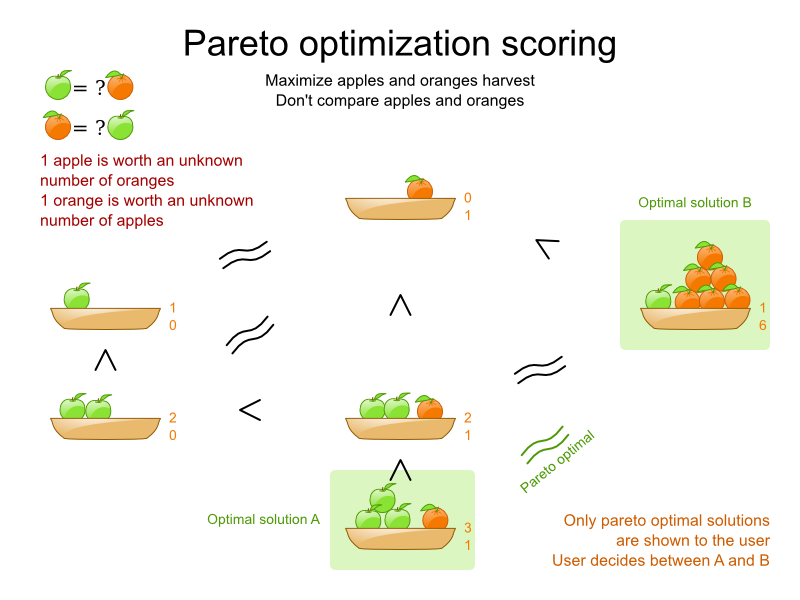
N Queens
- Hard constraints:
- -1 for every pair of conflicting queens
- Soft constraints:
- None

Score = -2
Conflicts: A-B, B-D

Score = 0
No conflicts
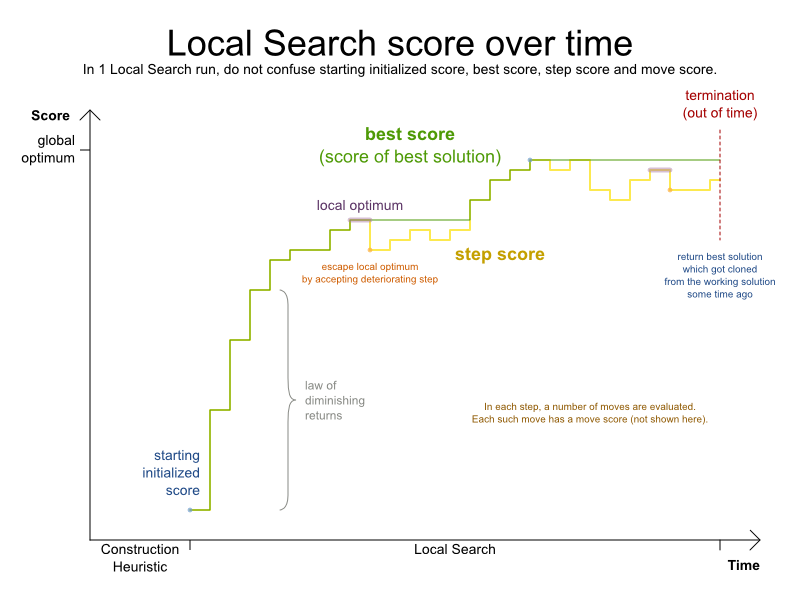
How do we find the best solution?
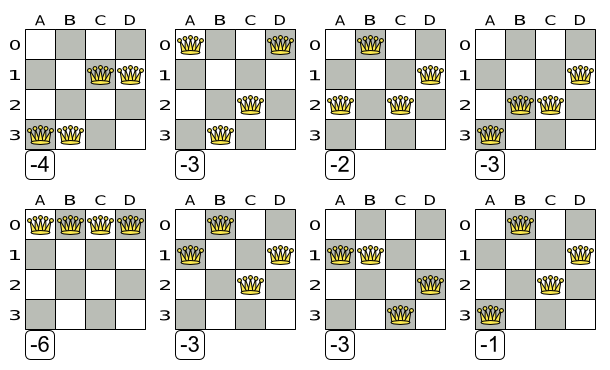
- Need for optimization algorithms
- Best solution in available time


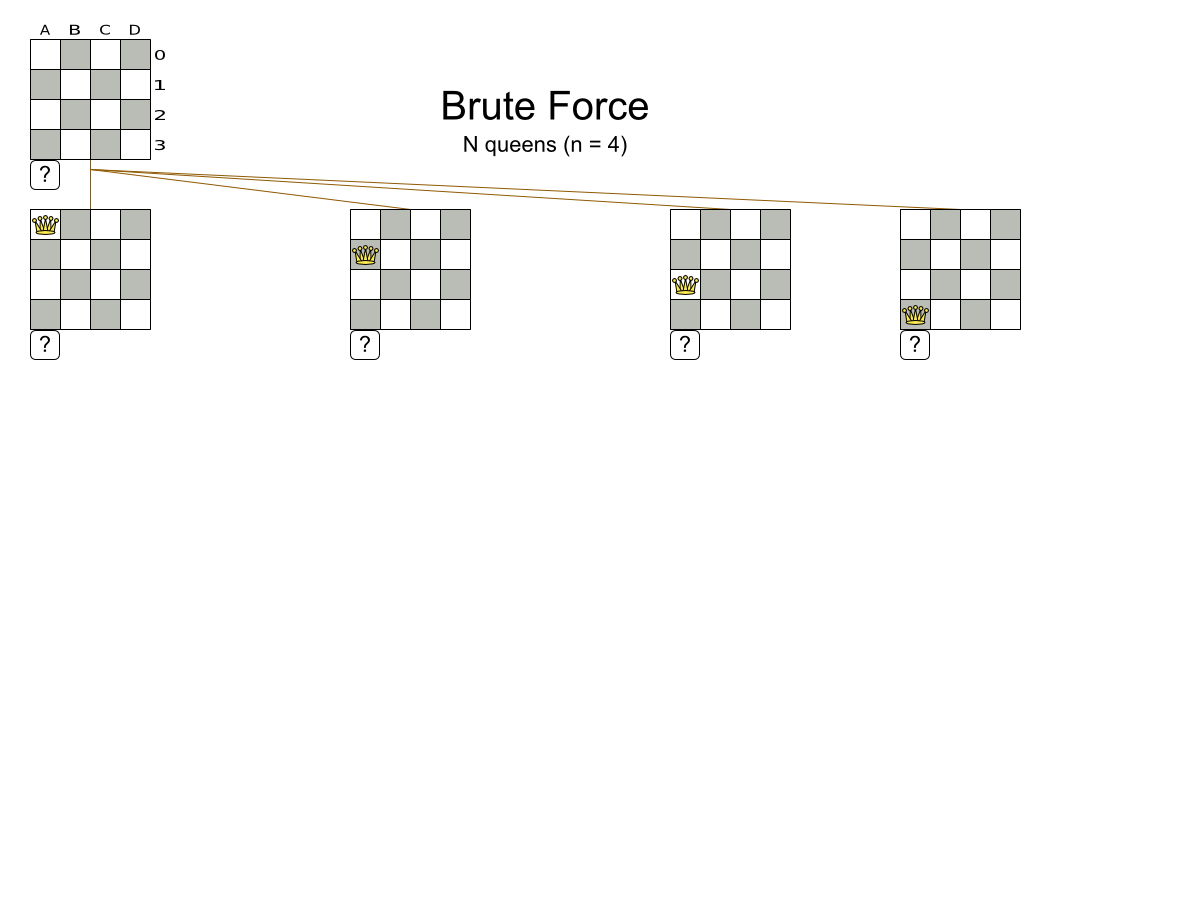
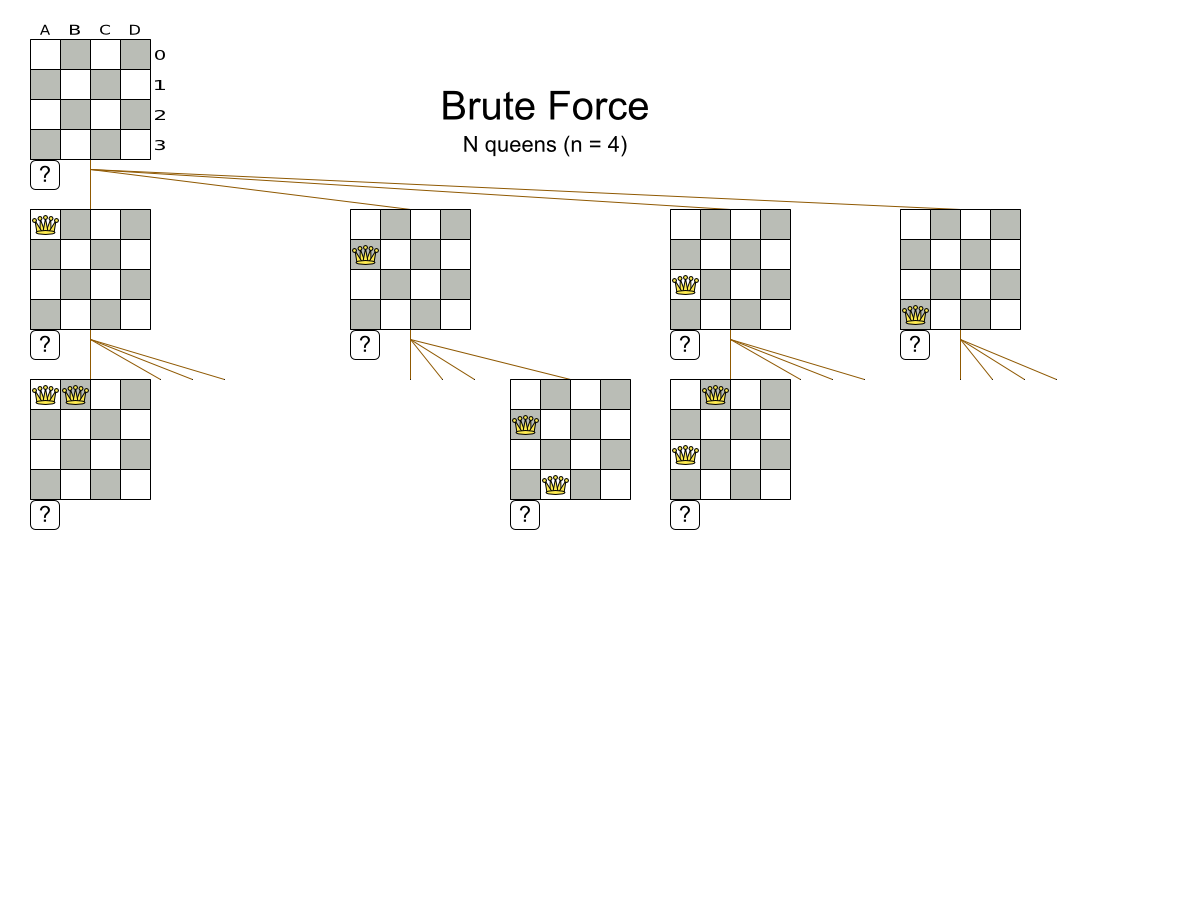
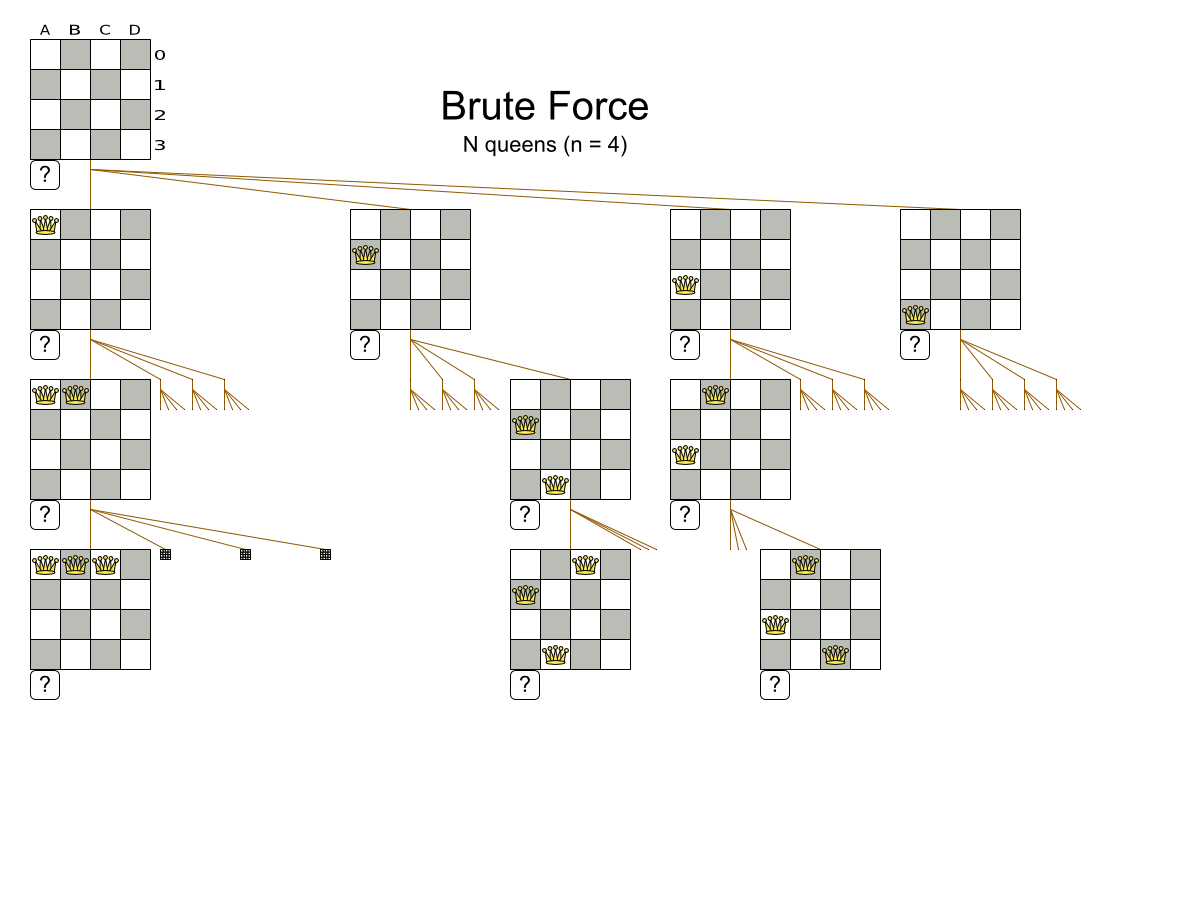
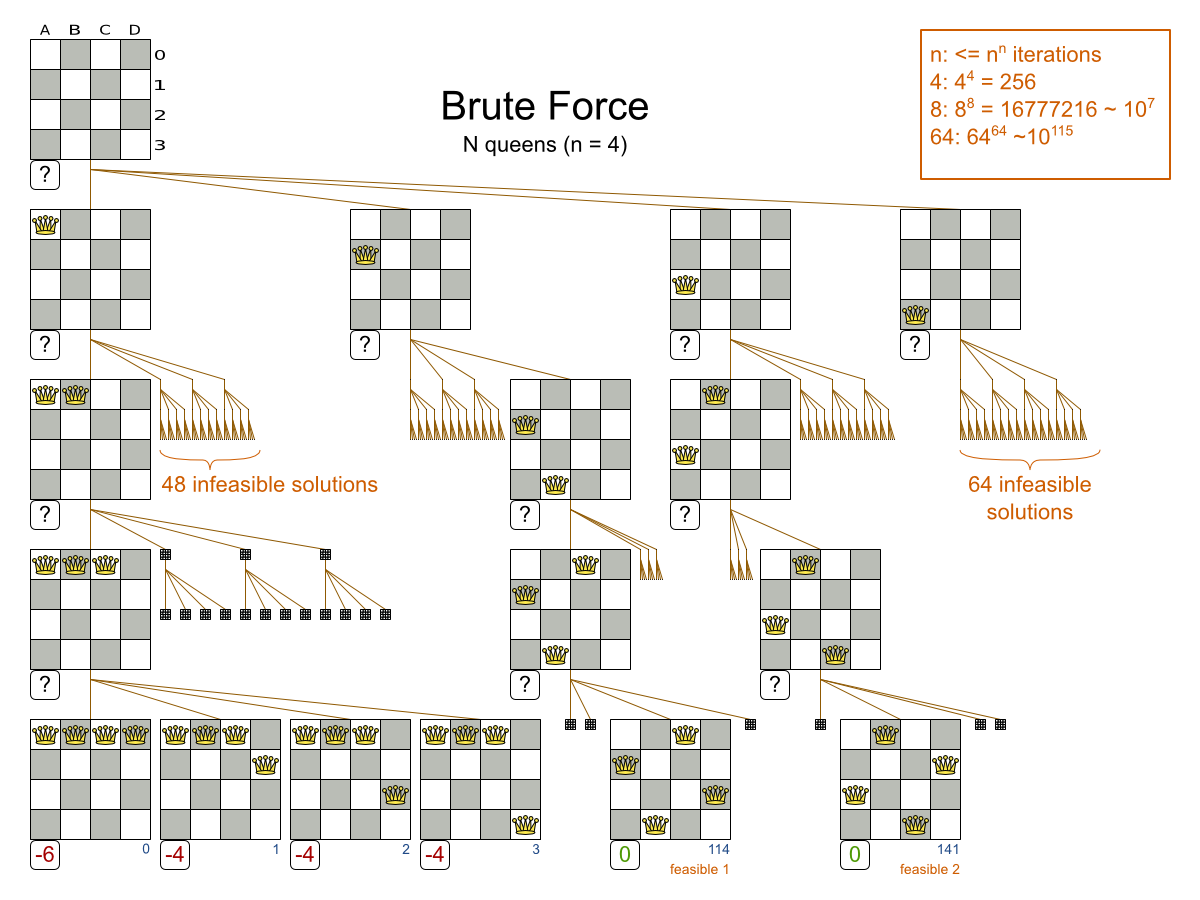
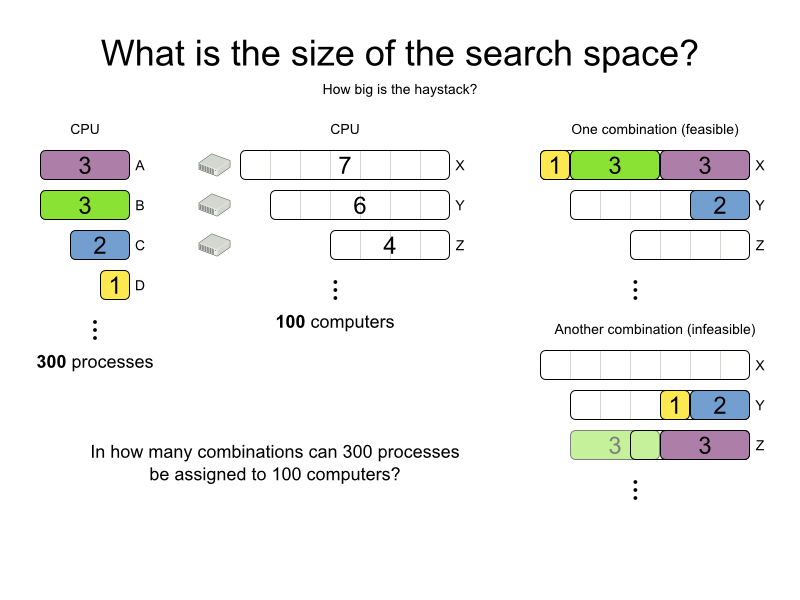
How many combinations
for 100 queens?

- 1 queen per column
- 100 queens ⇒ 100 variables
- 100 rows ⇒ 100 values per variable
Source: NASA (wikipedia)
> humans?
7 000 000 000
How many combinations
for 100 queens?

- 1 queen per column
- 100 queens ⇒ 100 variables
- 100 rows ⇒ 100 values per variable

Source: NASA and ESA (wikipedia)
> minimum atoms
in the observable universe?
1080
How many combinations
for 100 queens?

- 1 queen per column
- 100 queens ⇒ 100 variables
- 100 rows ⇒ 100 values per variable
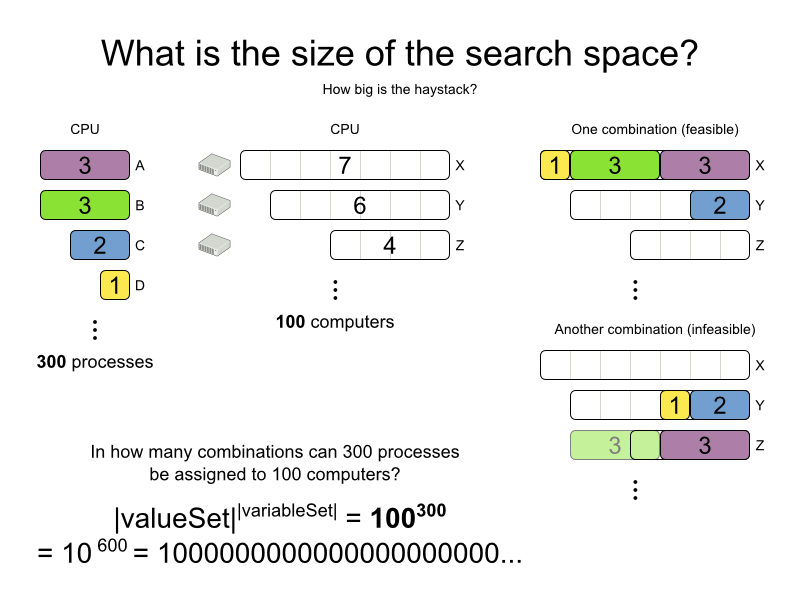
100100 = 10200
1 0000000000 0000000000 0000000000 0000000000 0000000000
0000000000 0000000000 0000000000 0000000000 0000000000
0000000000 0000000000 0000000000 0000000000 0000000000
0000000000 0000000000 0000000000 0000000000 0000000000
How many combinations
for n queens?

- 1 queen per column
- n queens ⇒ n variables
- n rows ⇒ n values per variable
nn
|valueSet||variableSet|
How long?
Presume 109 scores/ms ⇒ 1020 scores/year
| Queens | Combinations | Calculation time |
|---|---|---|
| 100 | 100100 = 10200 | 10180 years |
| 1000 | 10001000 = 103000 | 102980 years |
| 10000 | 1000010000 = 1040000 | 1039980 years |
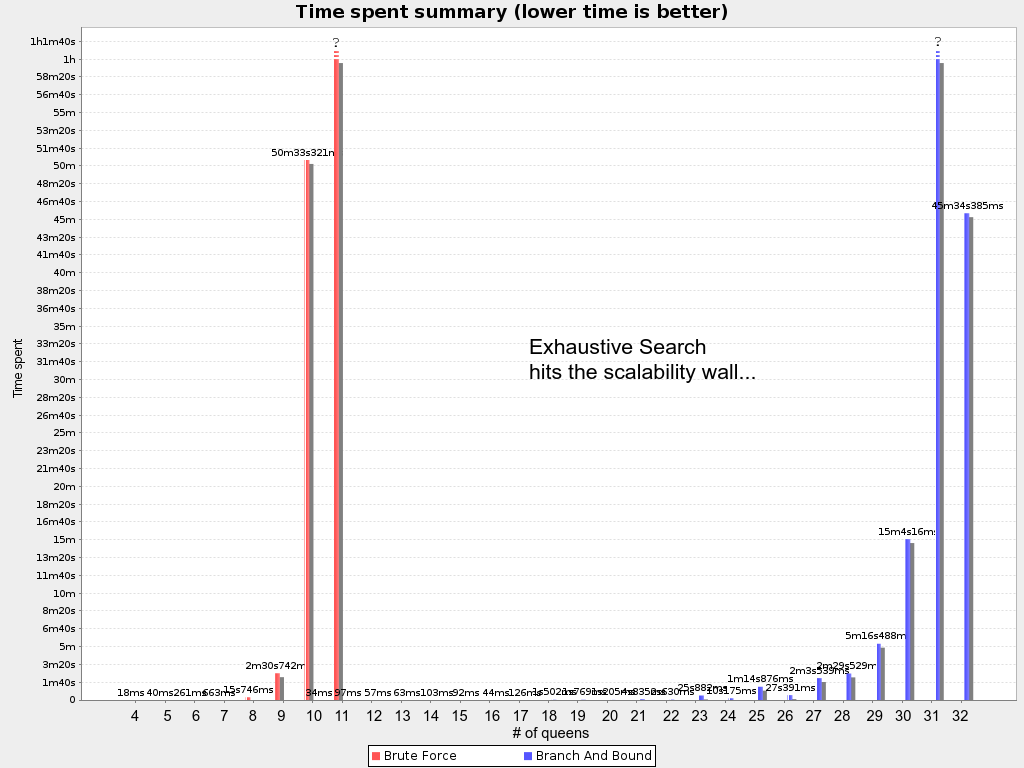
Moore's law == a drop in the ocean

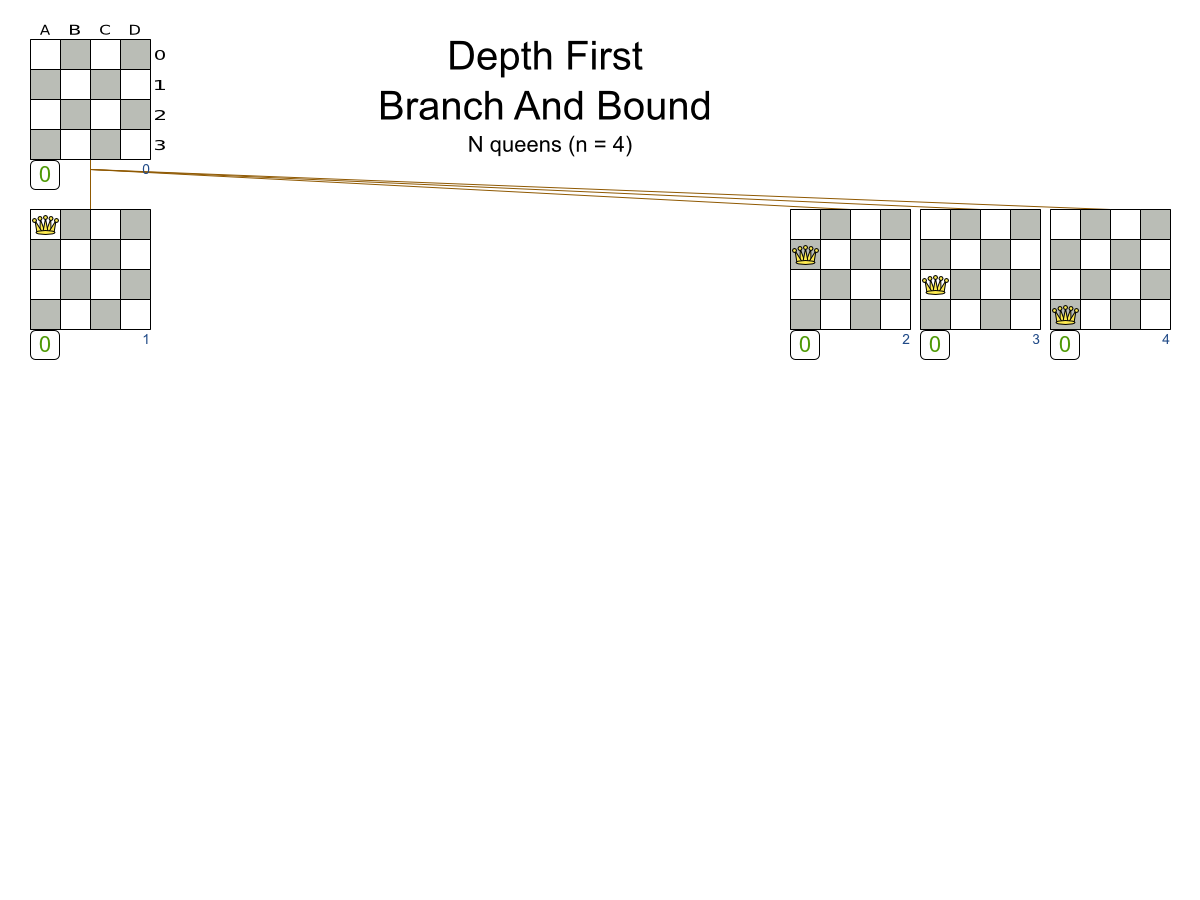
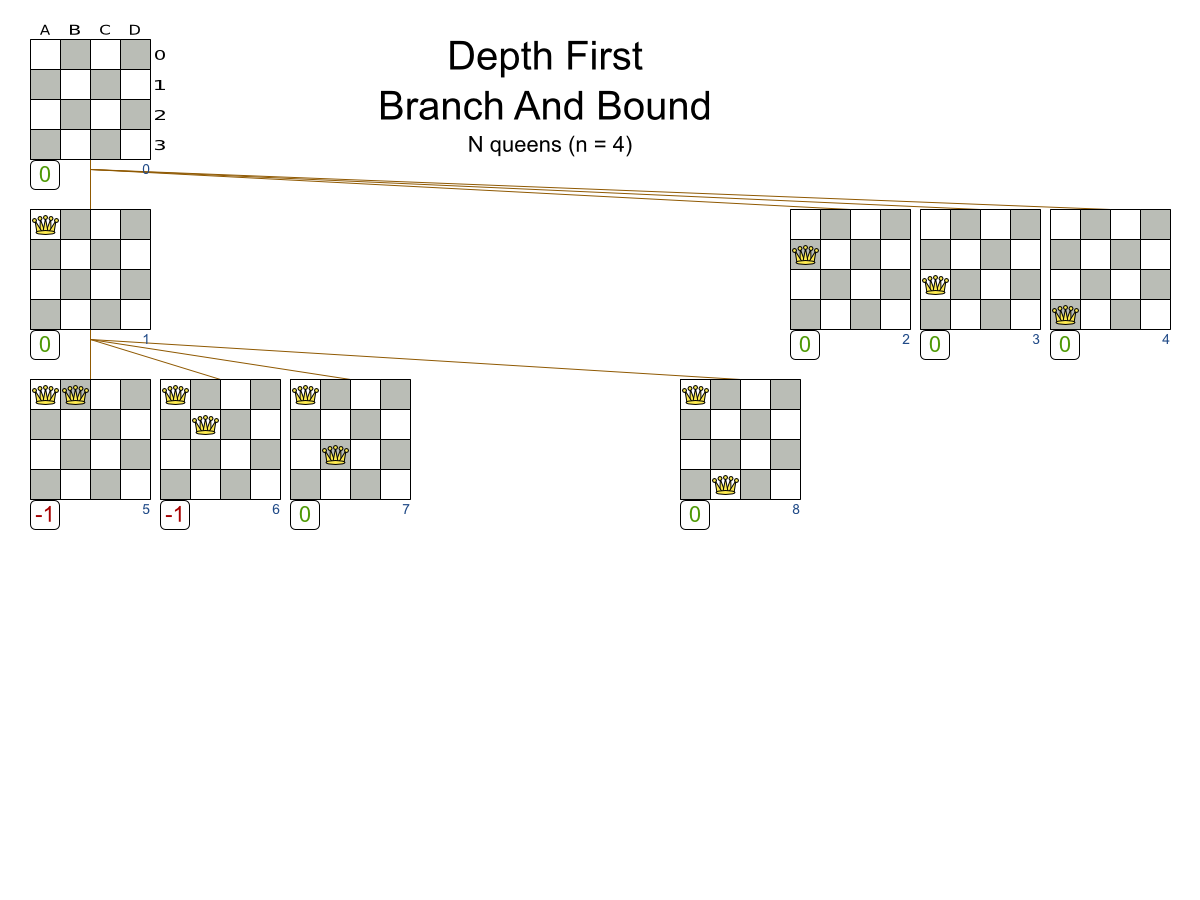
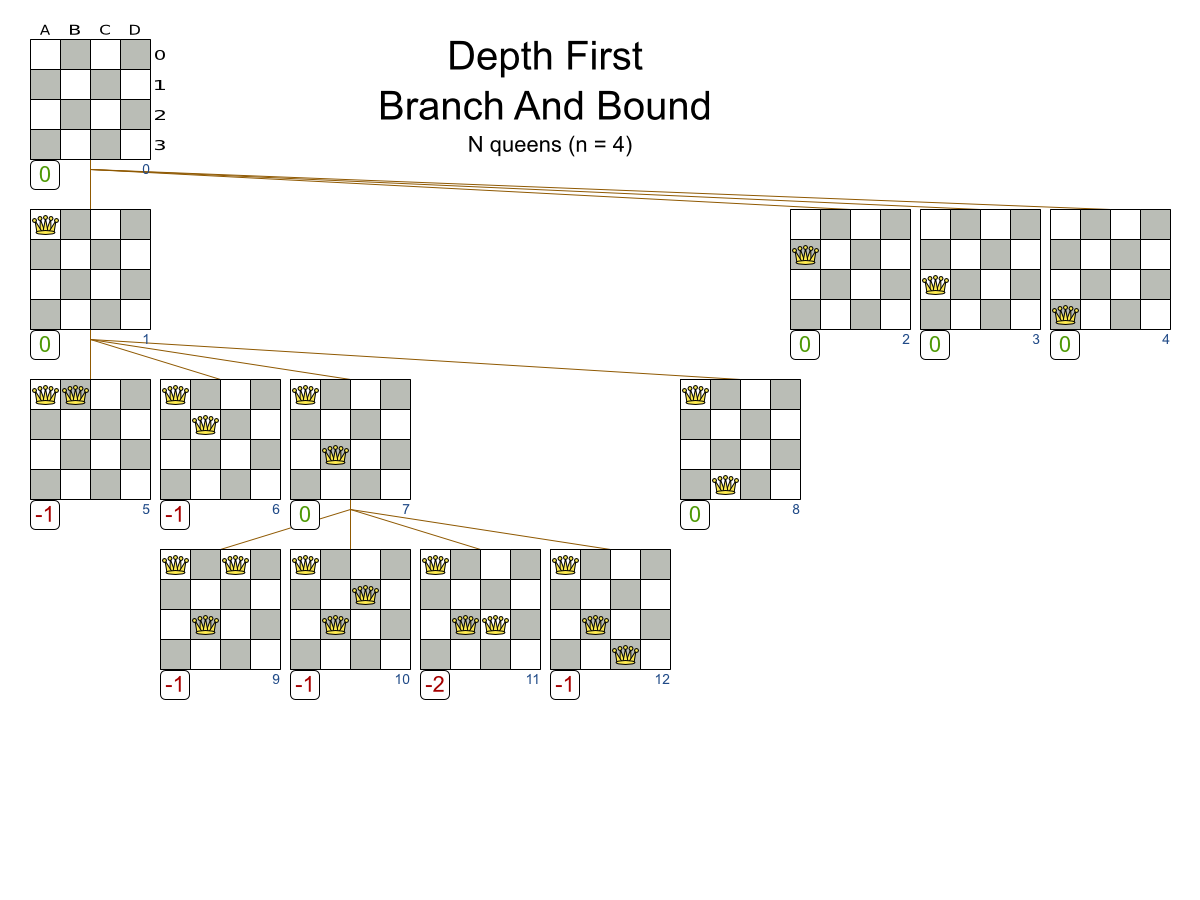
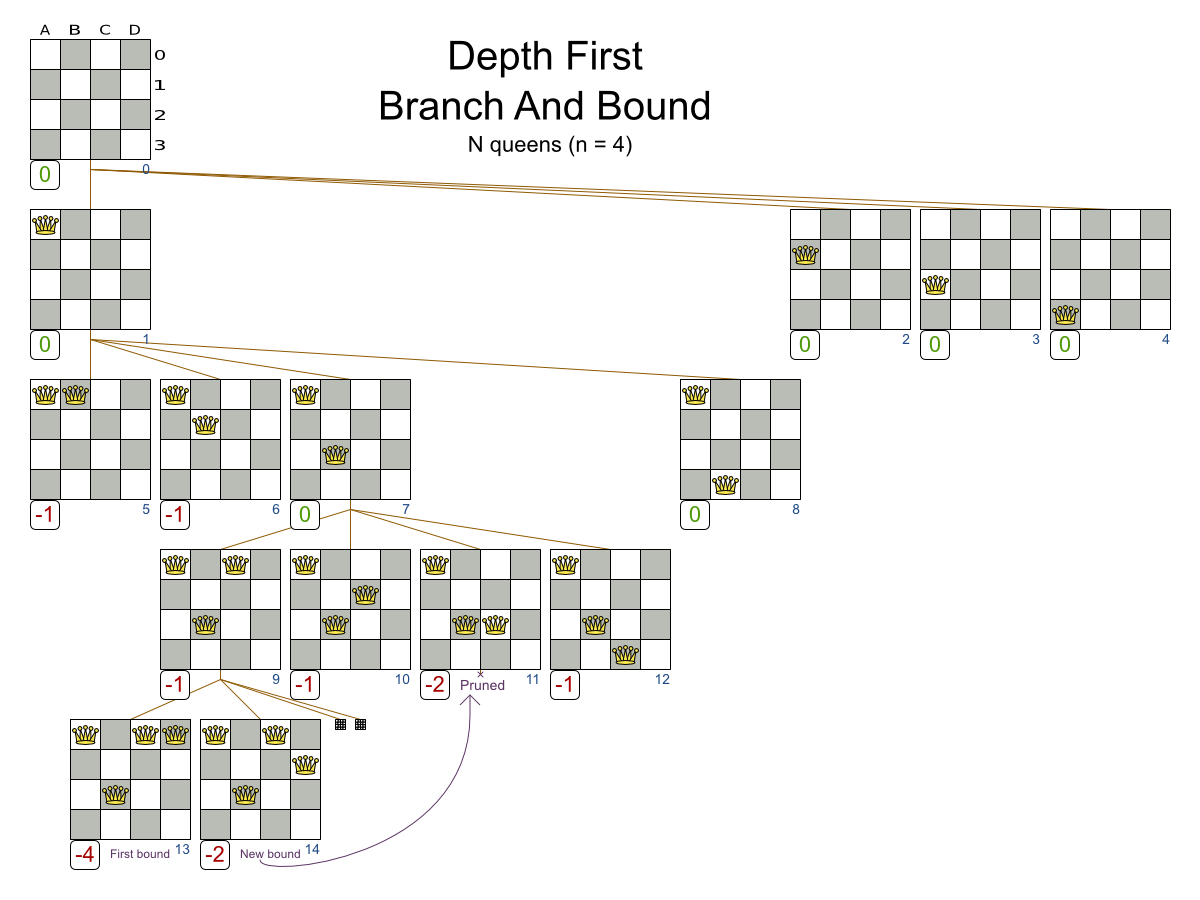
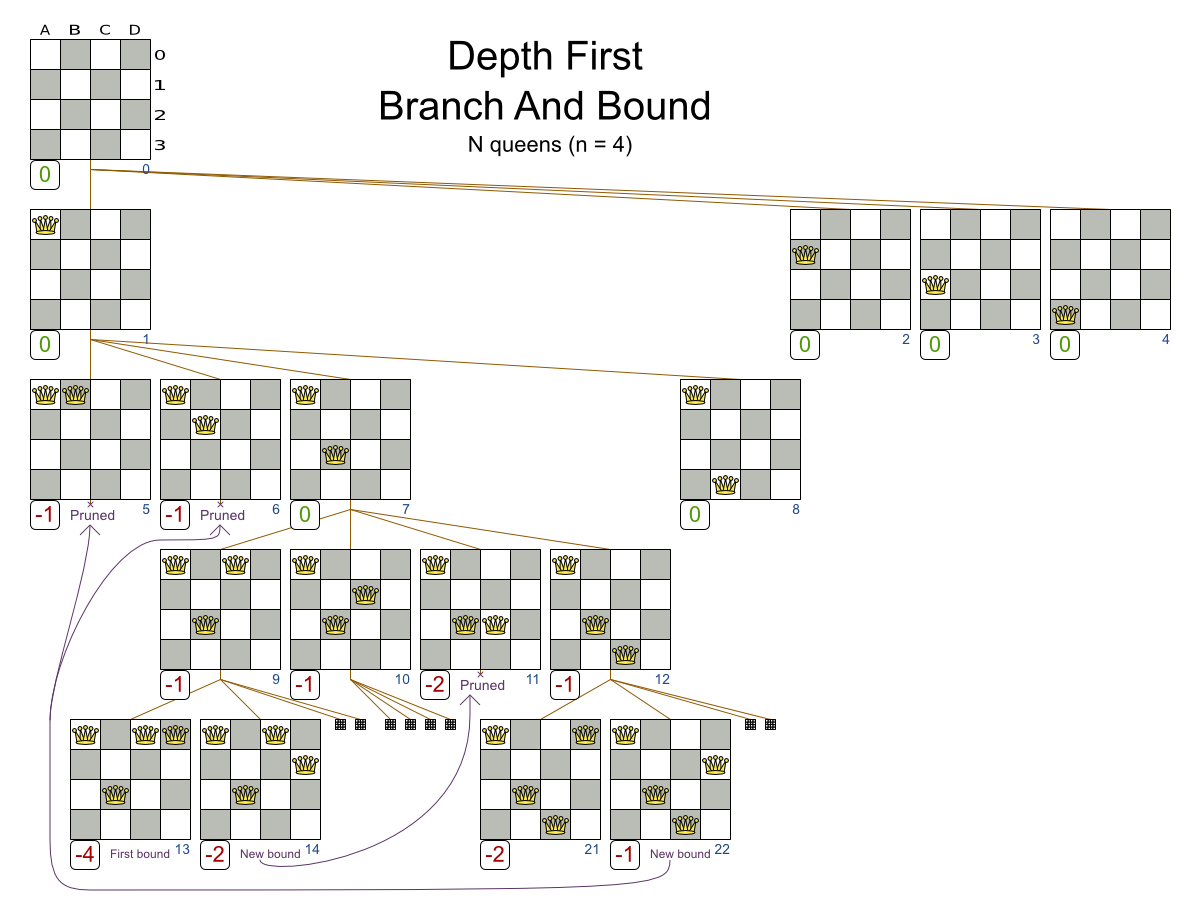
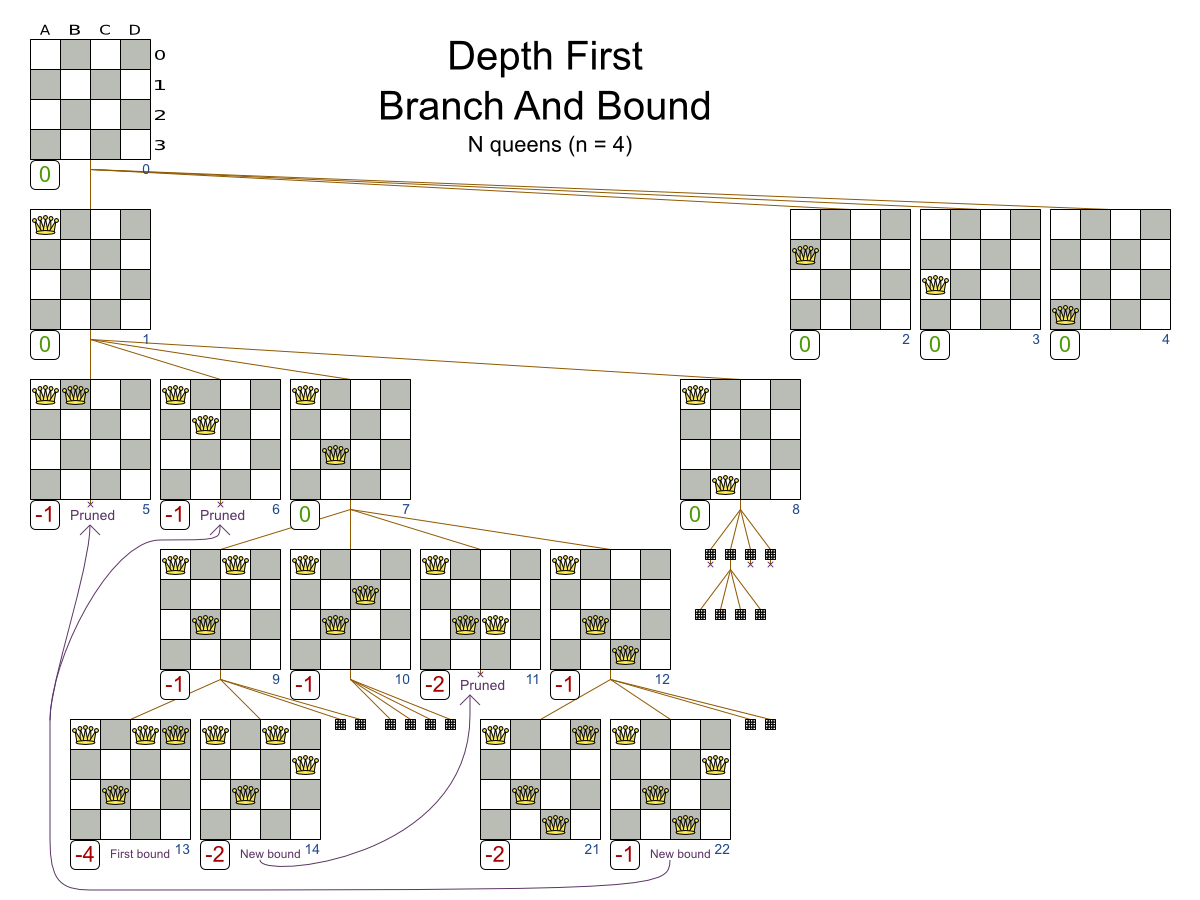
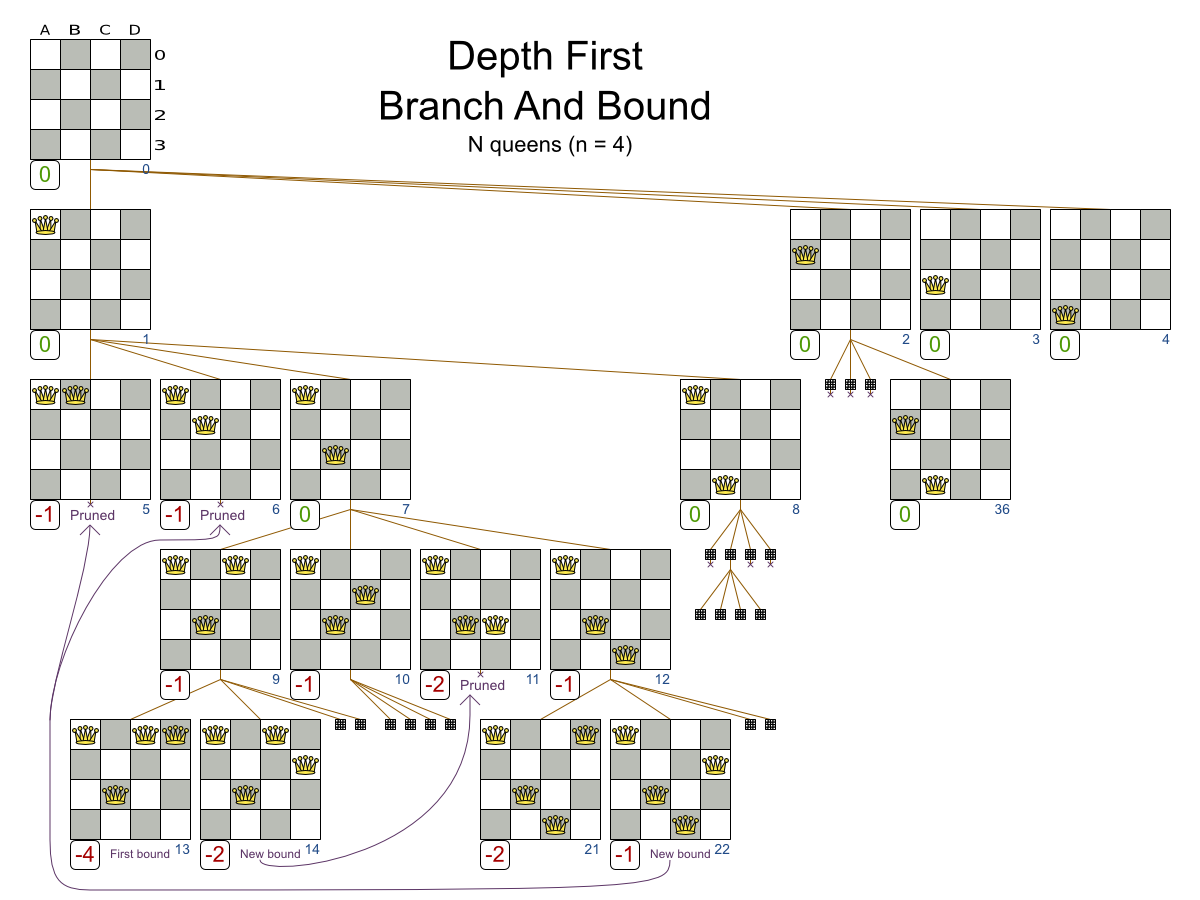
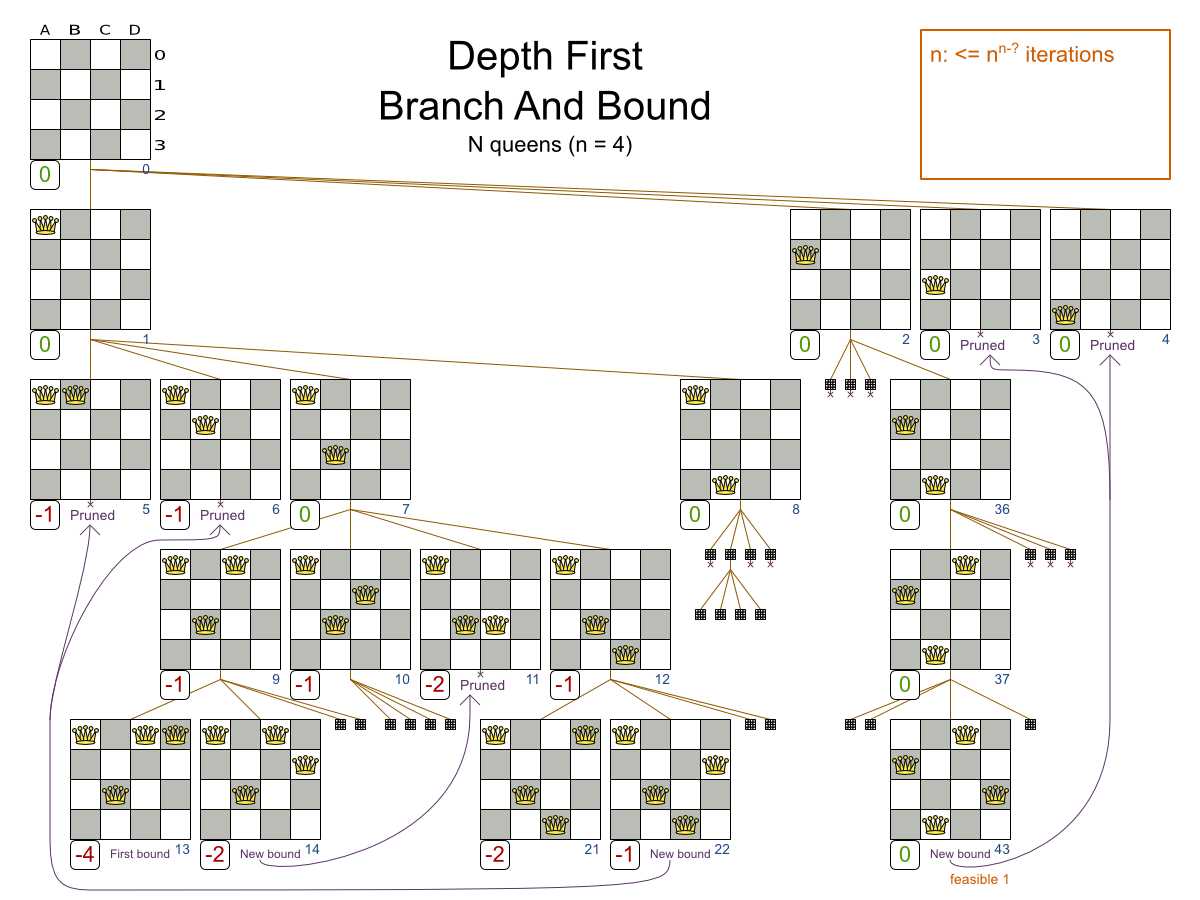
Exhaustive Search scalability

8 queens = 15.7 seconds
9 queens = 2.5 minutes (times 10)
10 queens = 0.83 hours (times 20)
Exhaustive Search doesn't scale
- Branches explode exponentially
- Not enough CPU
- Not enough memory



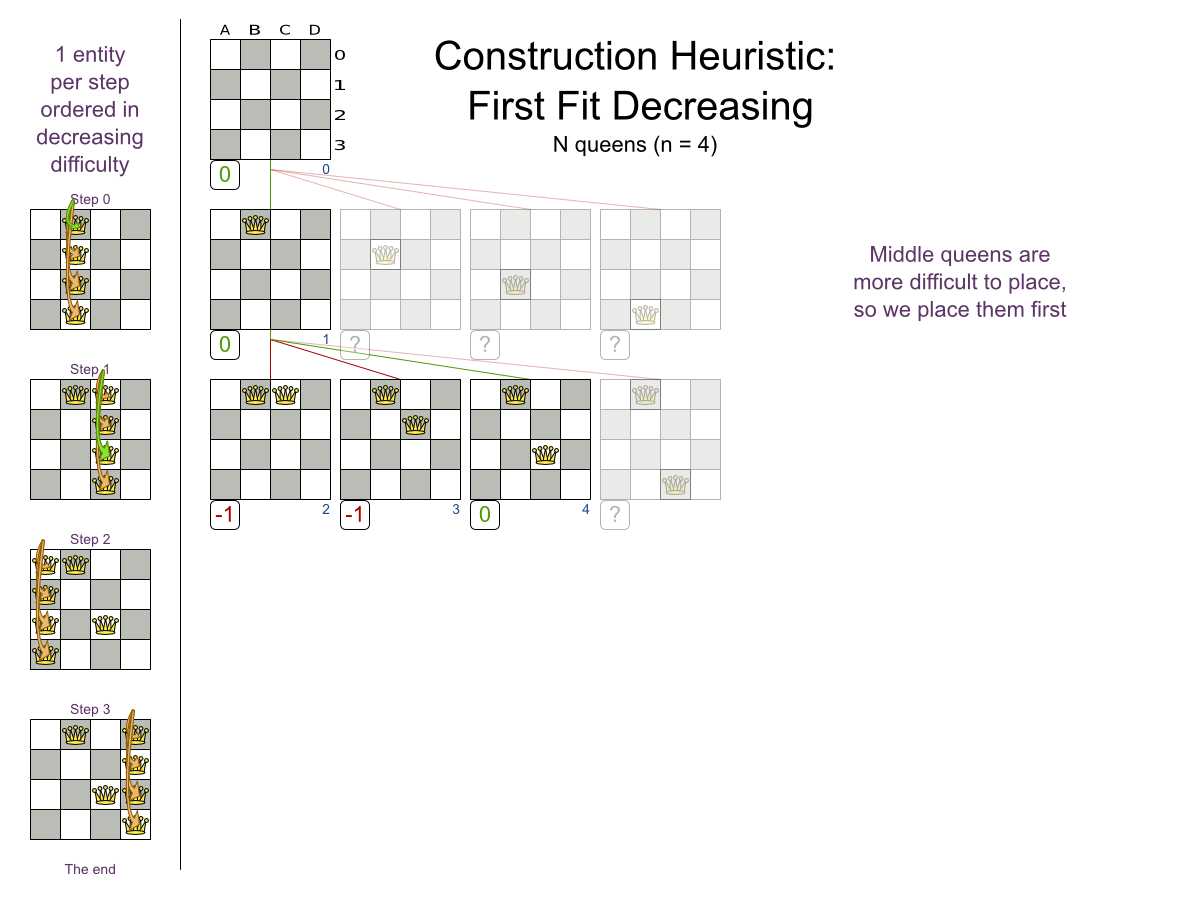
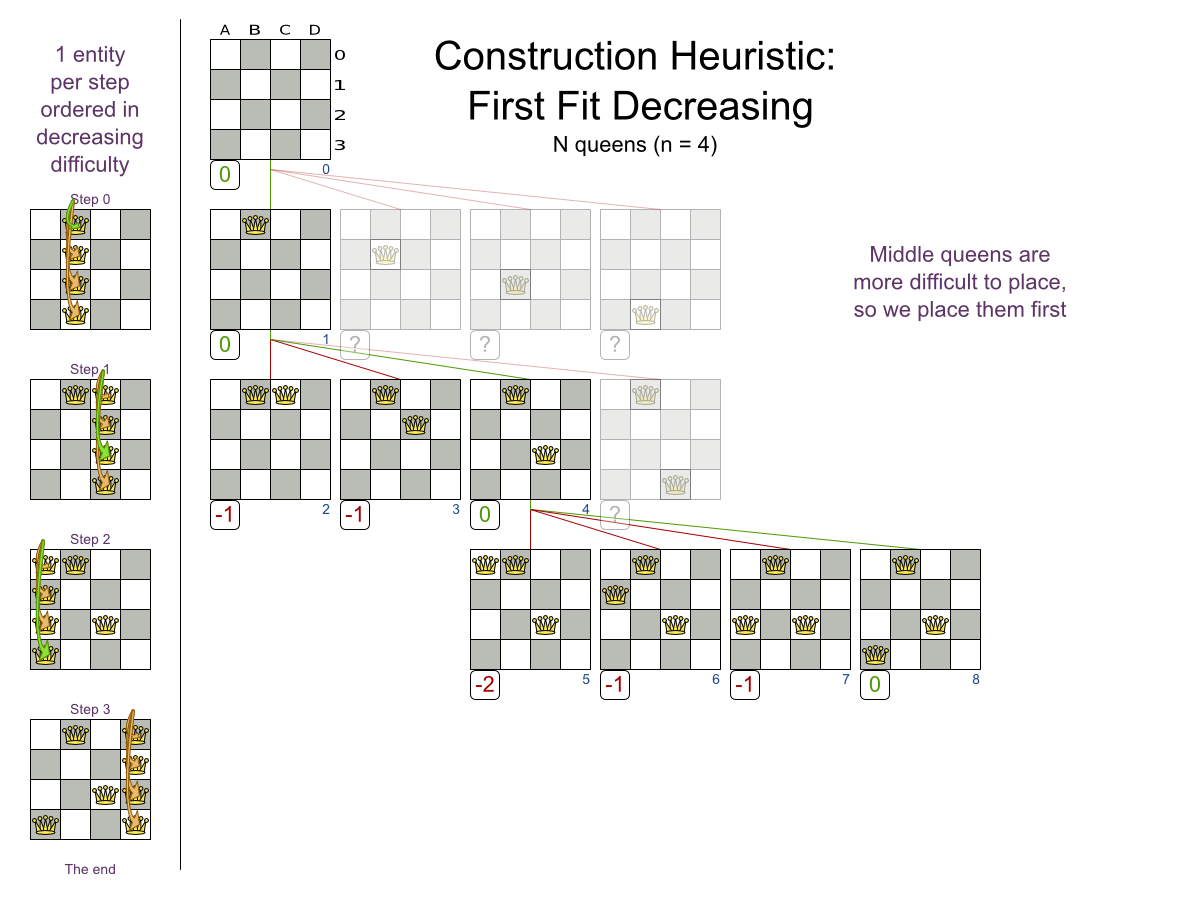
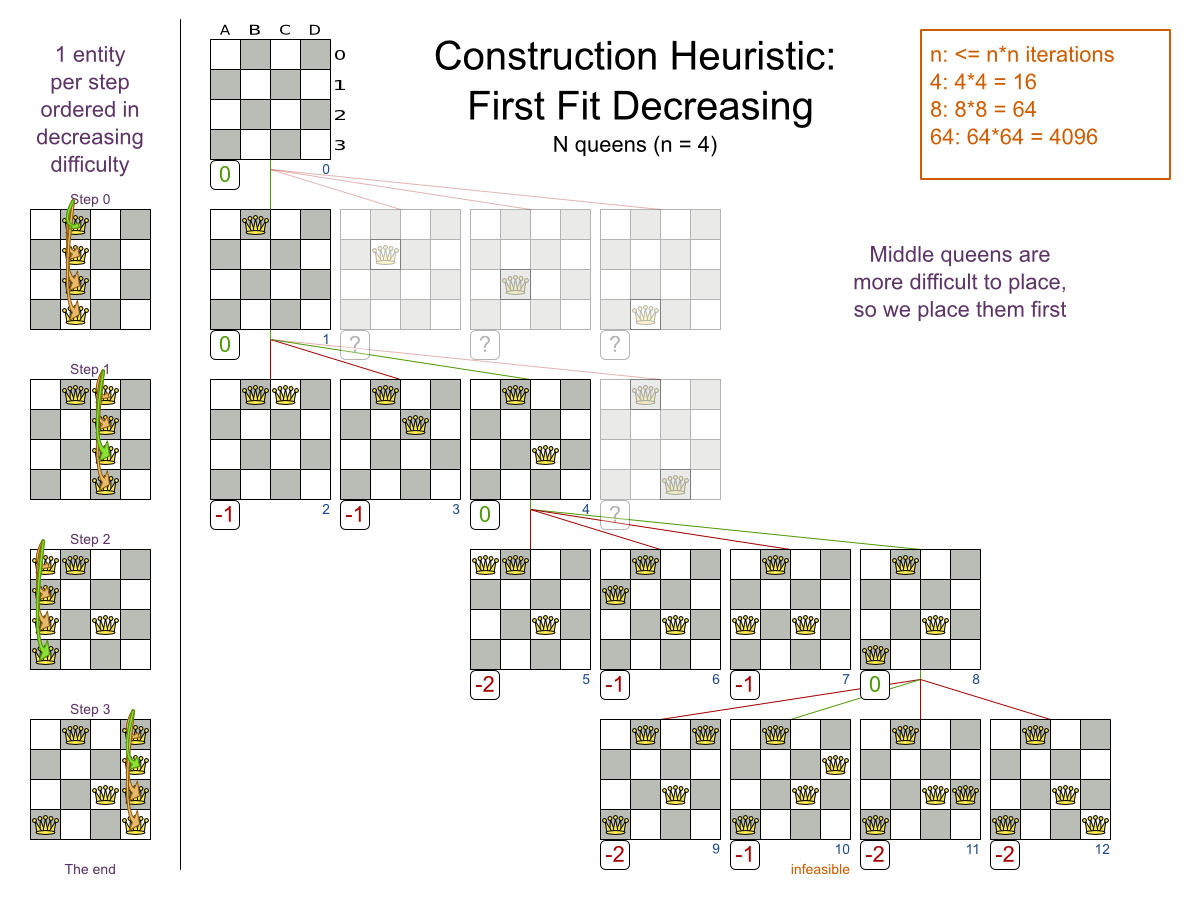
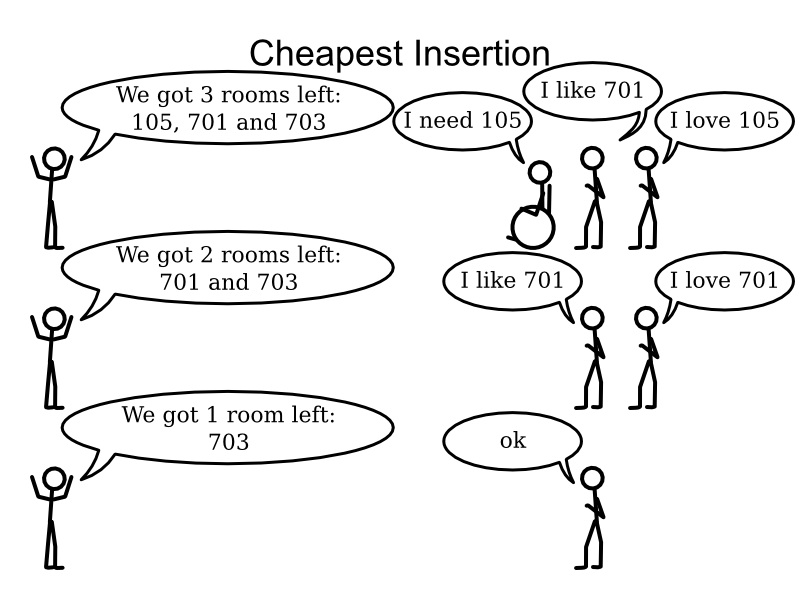
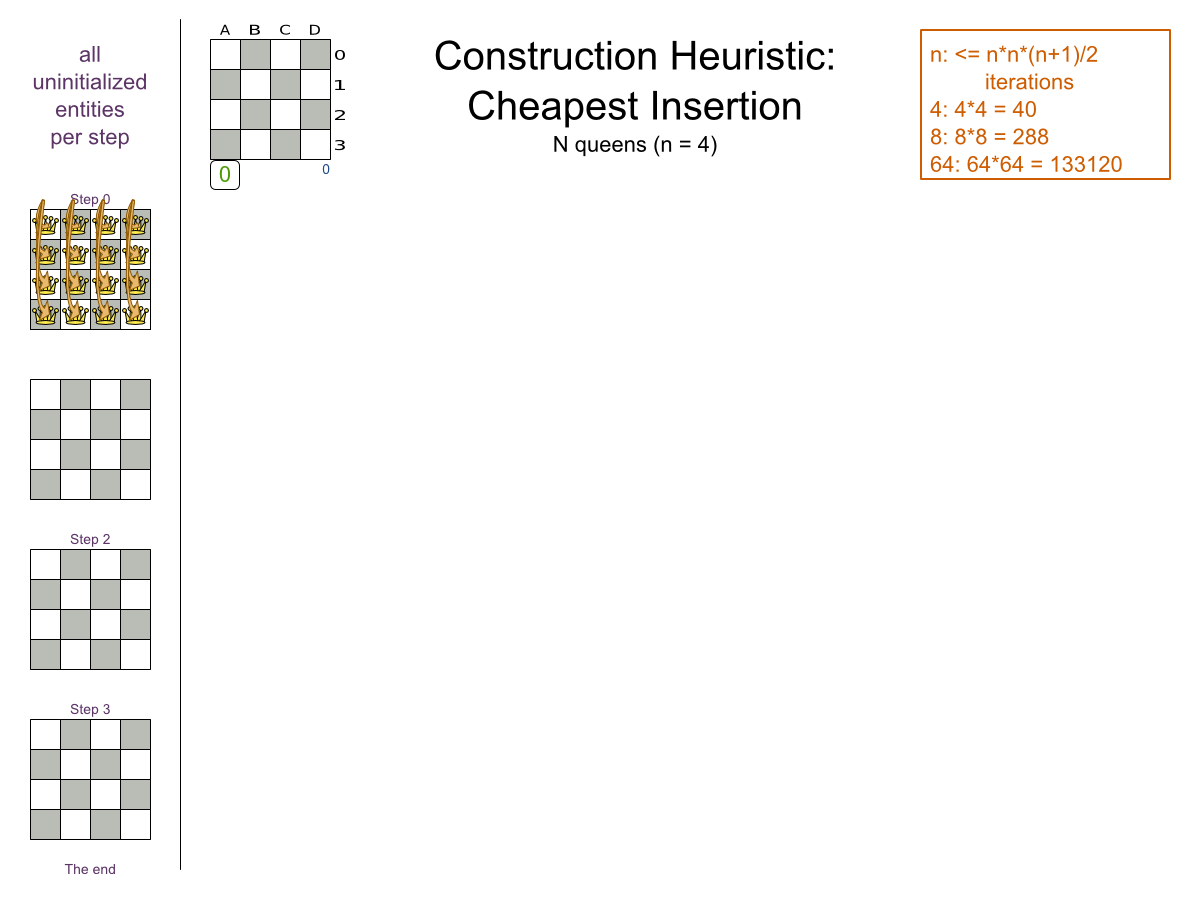
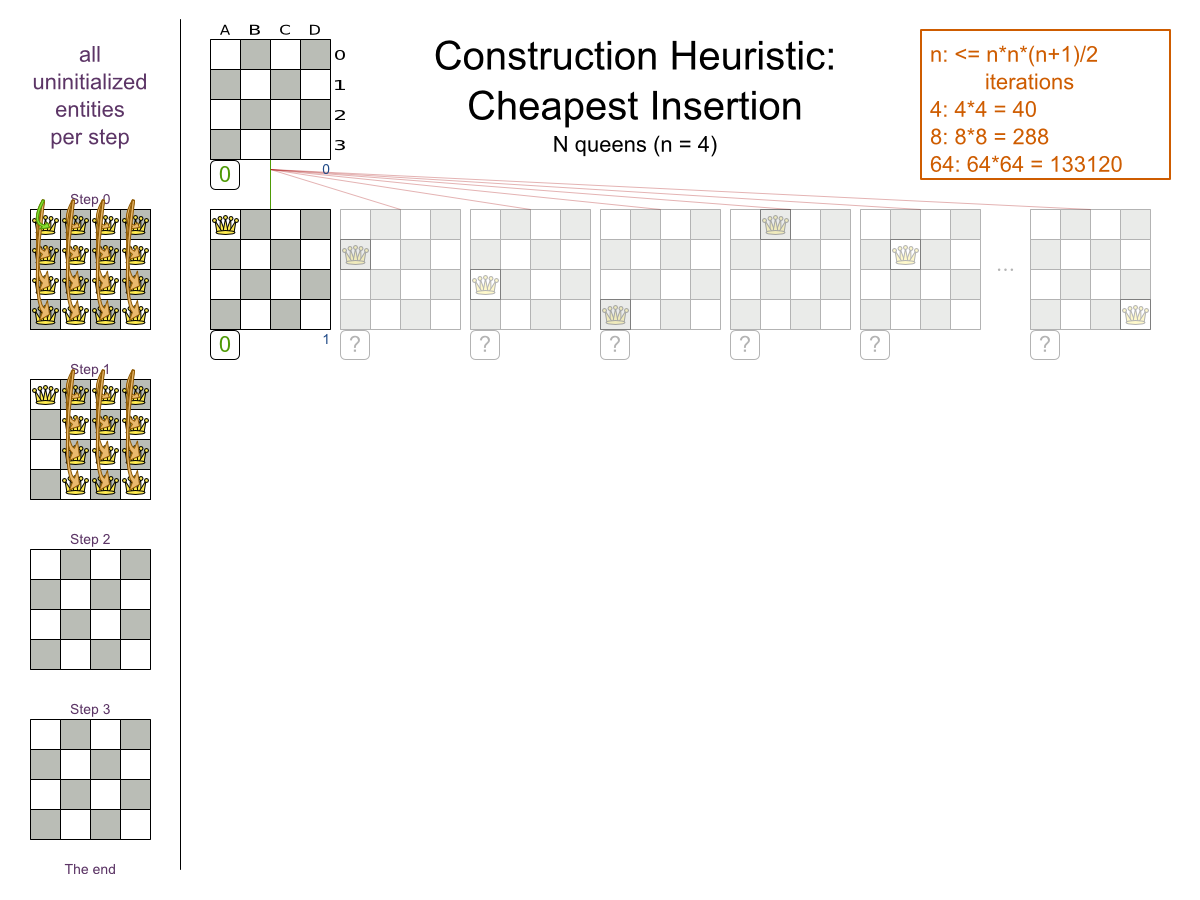
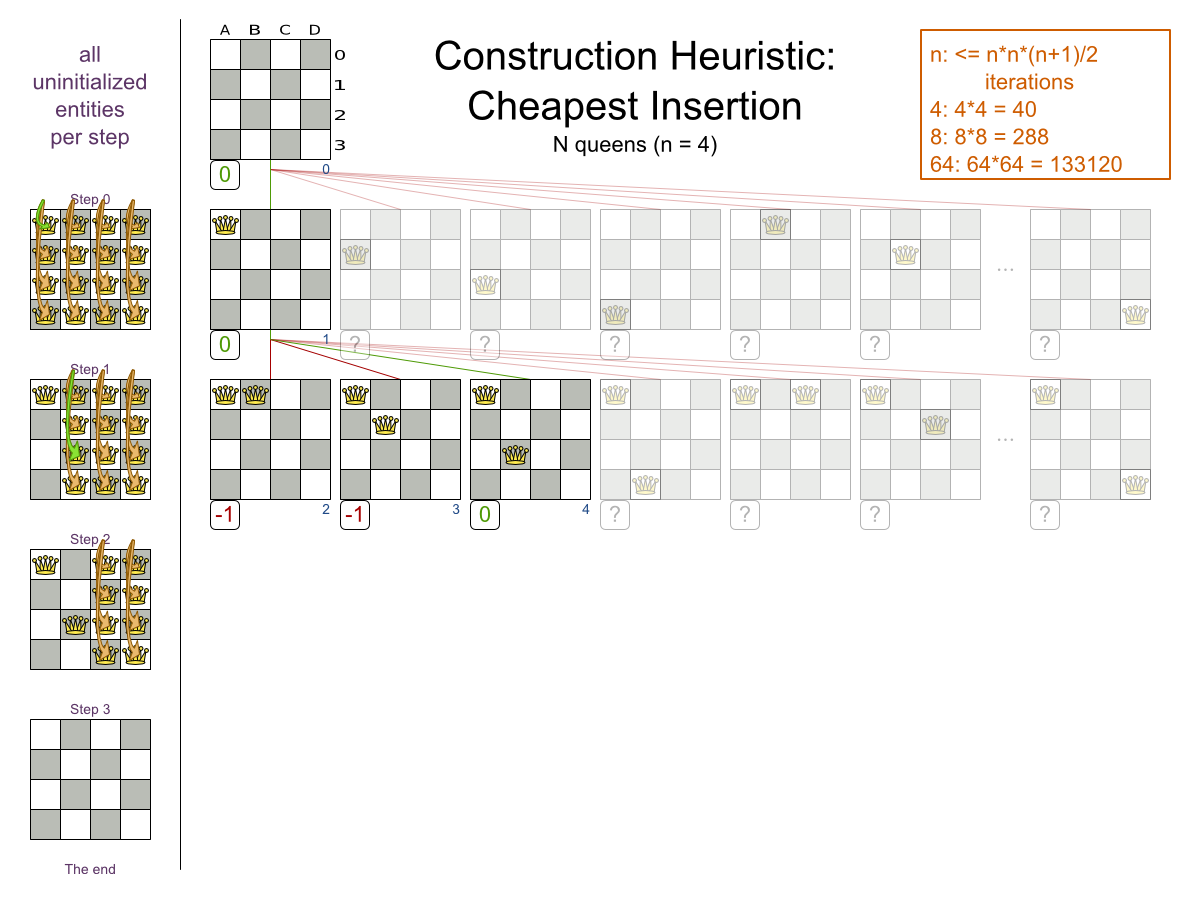
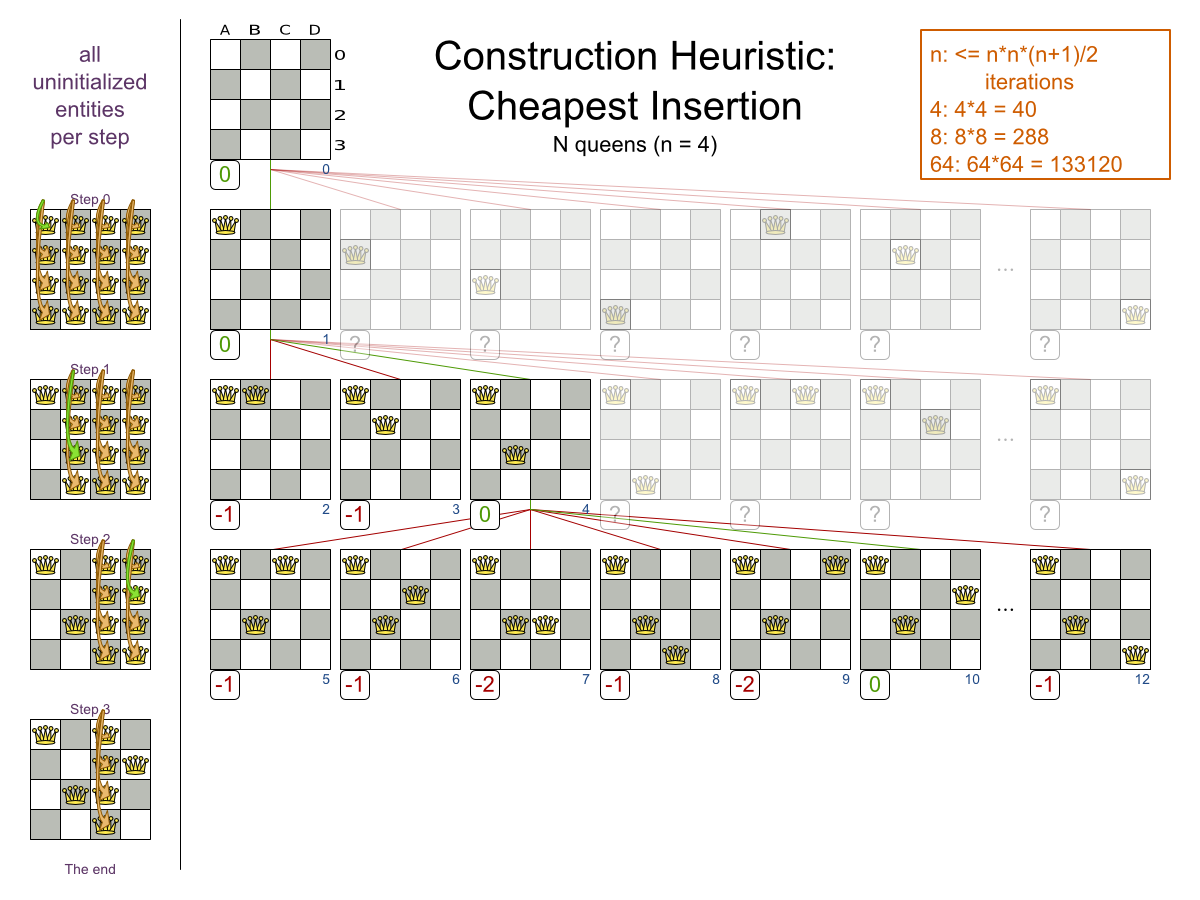
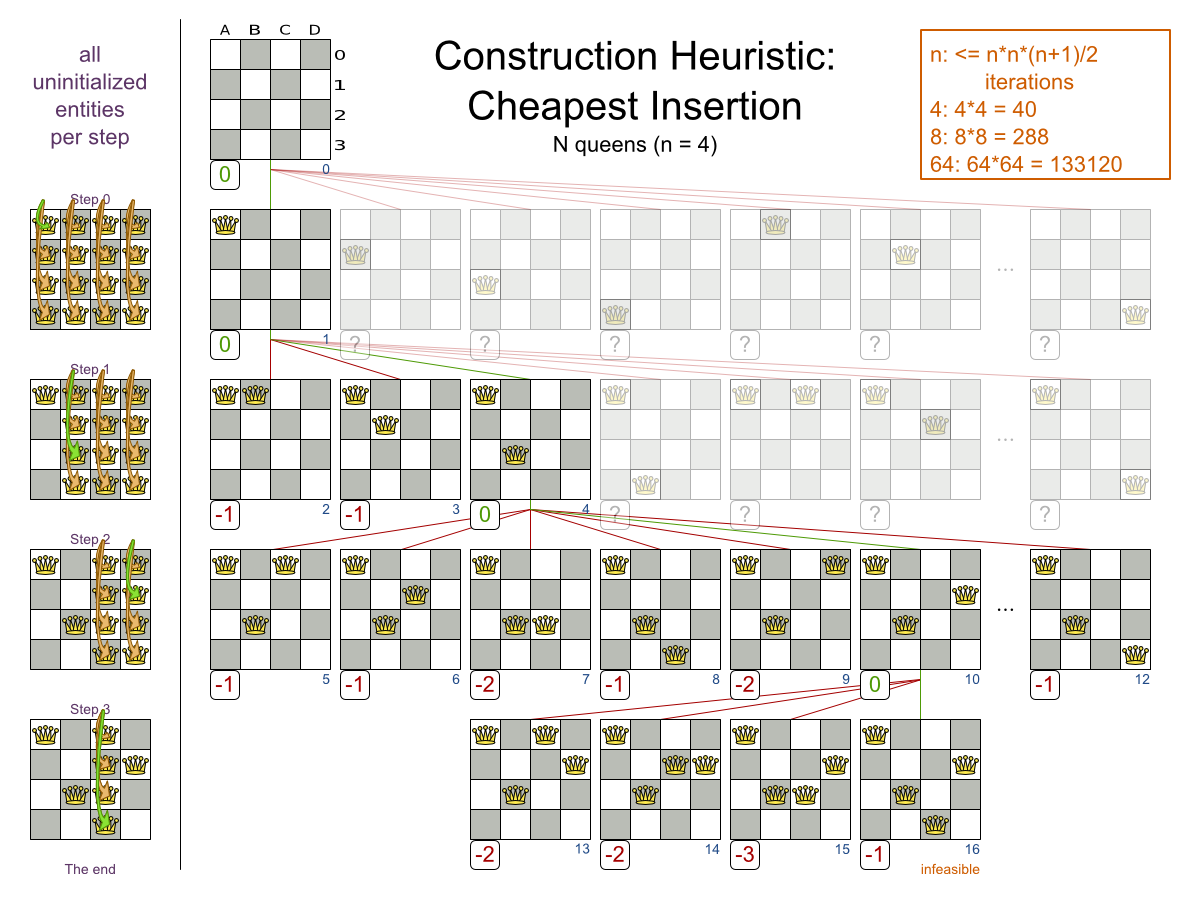
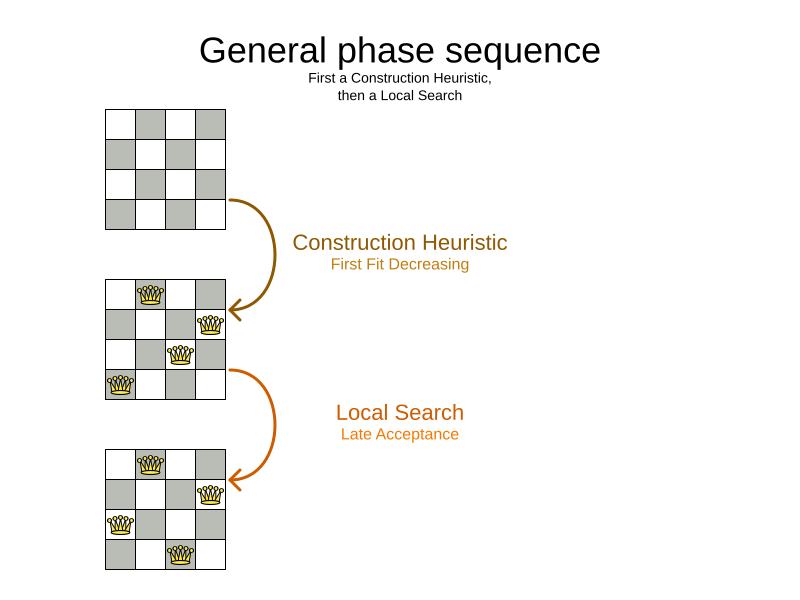
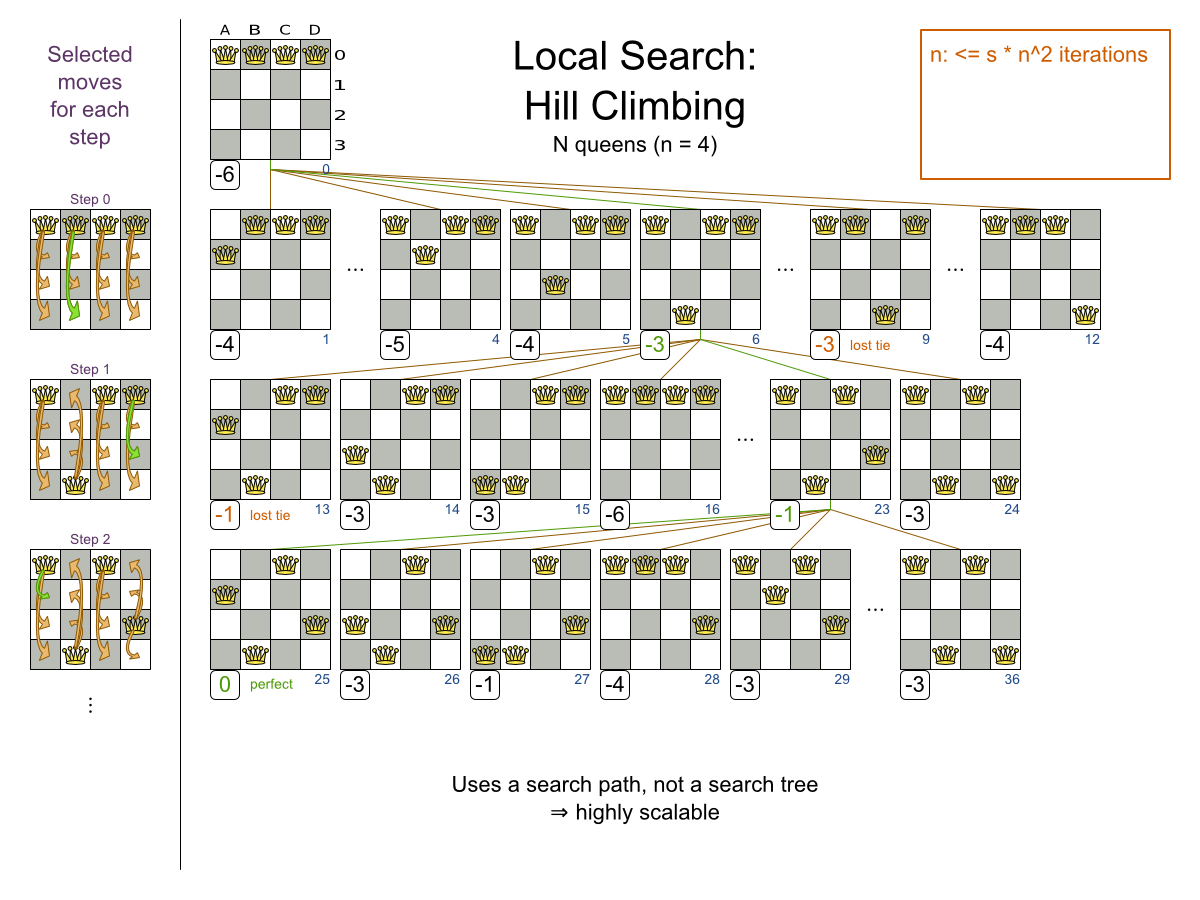
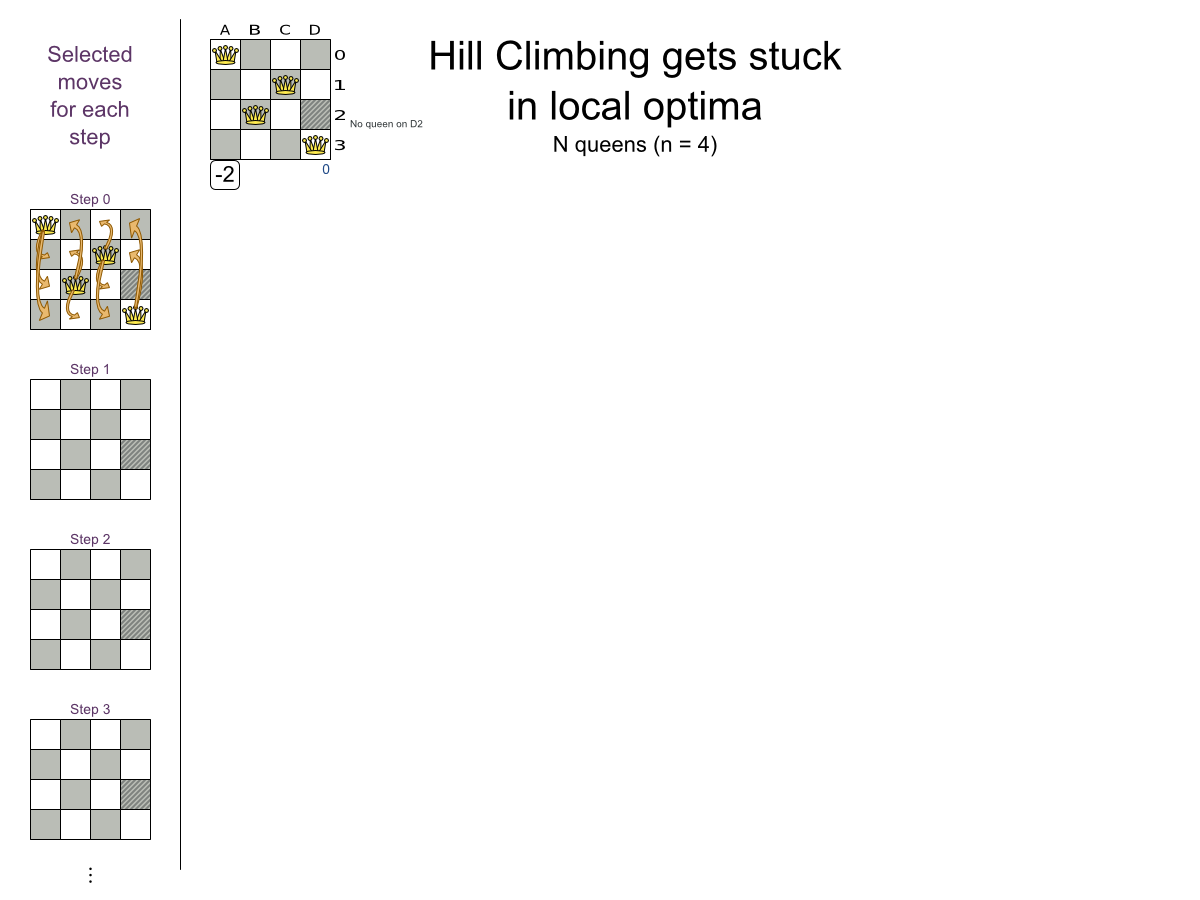
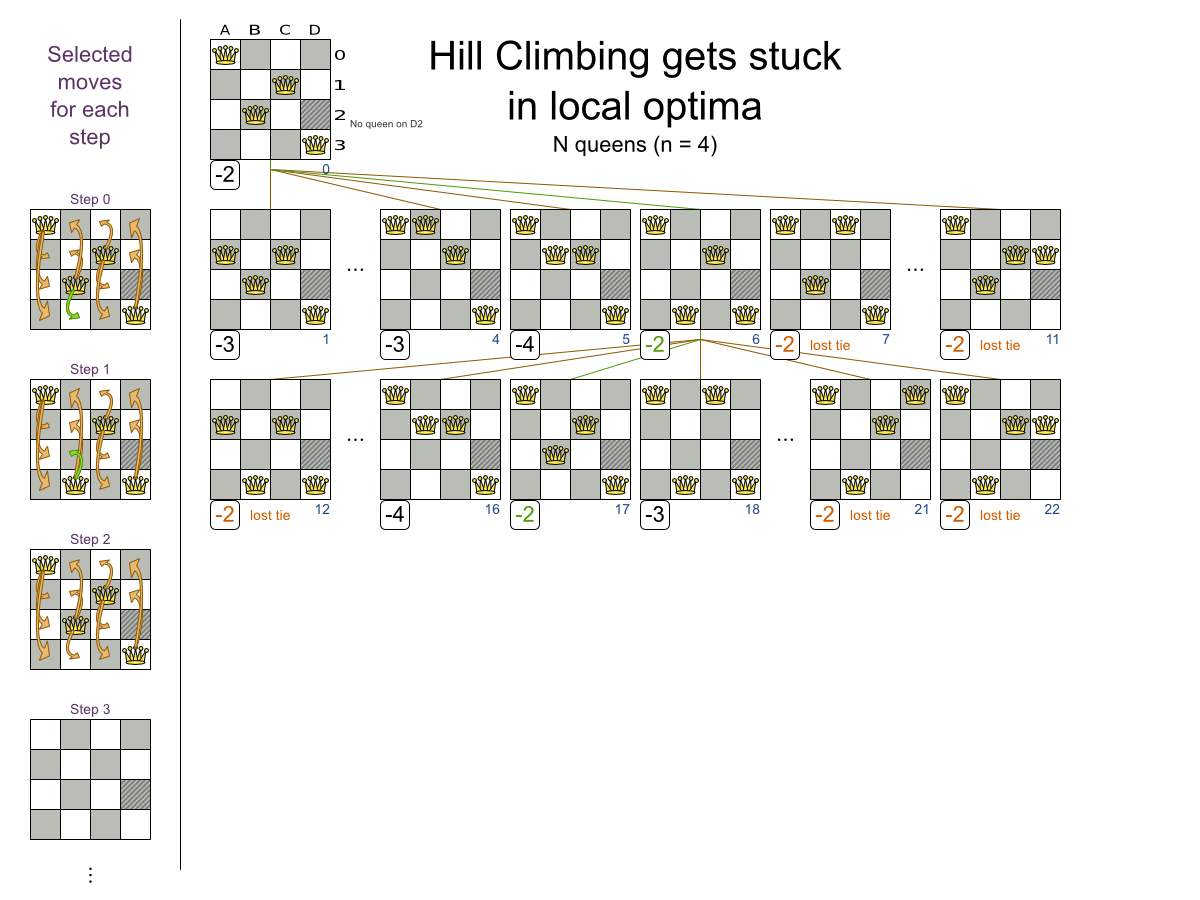
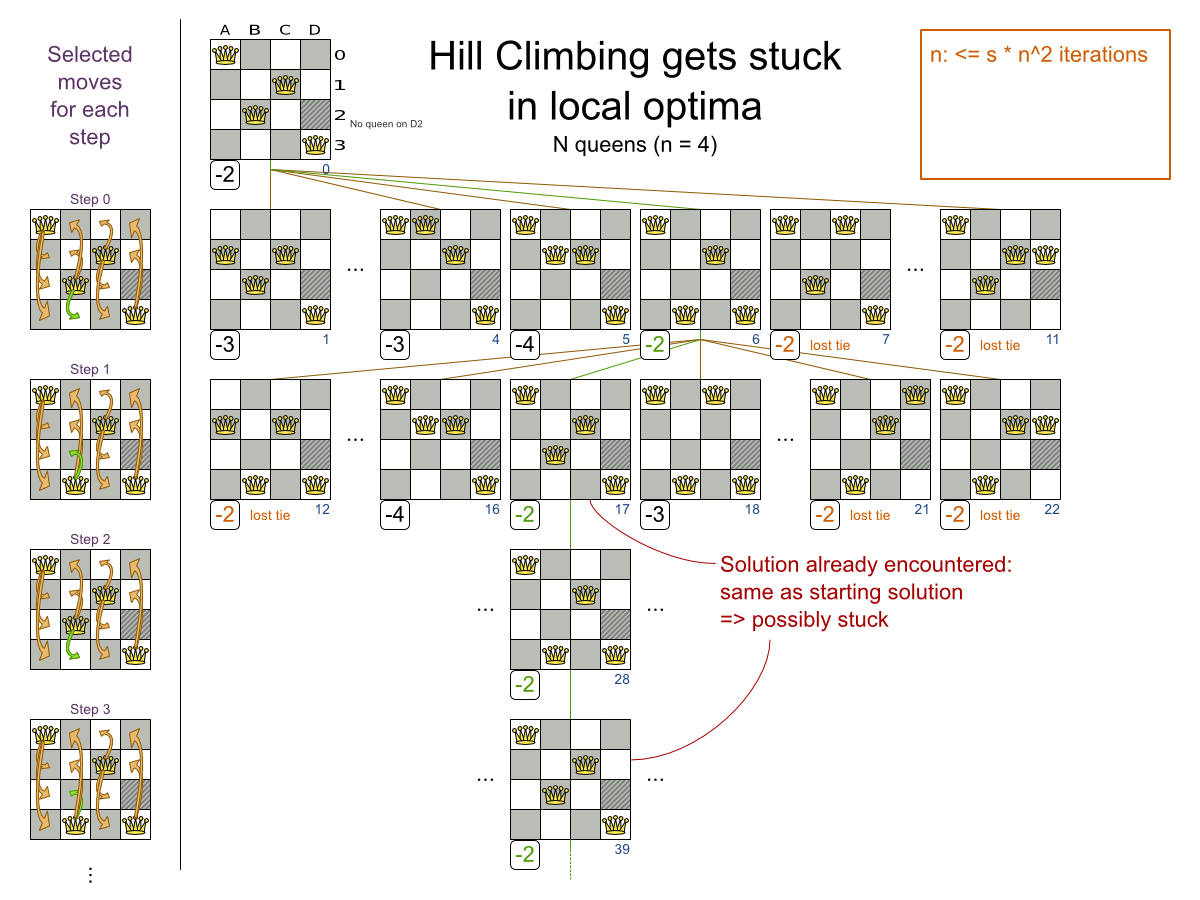
Local Search:
Move types
- Change move
- Swap move
- ...
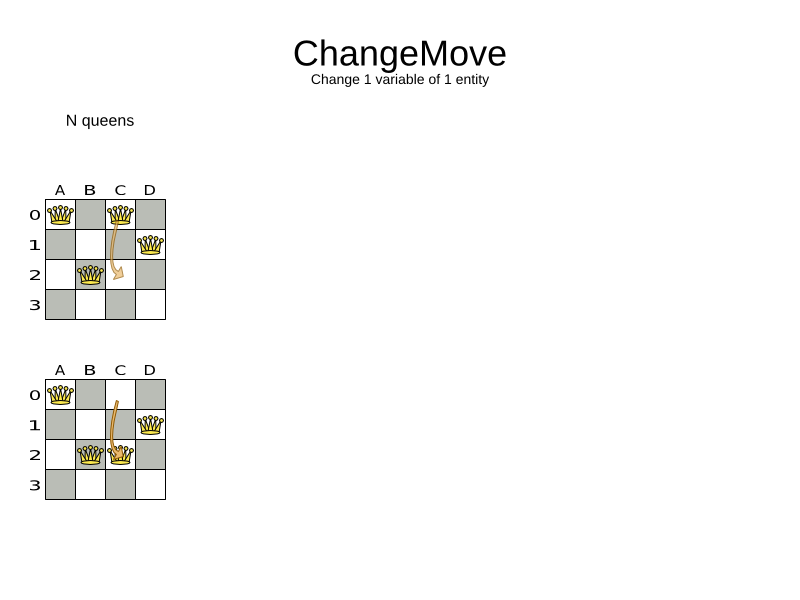
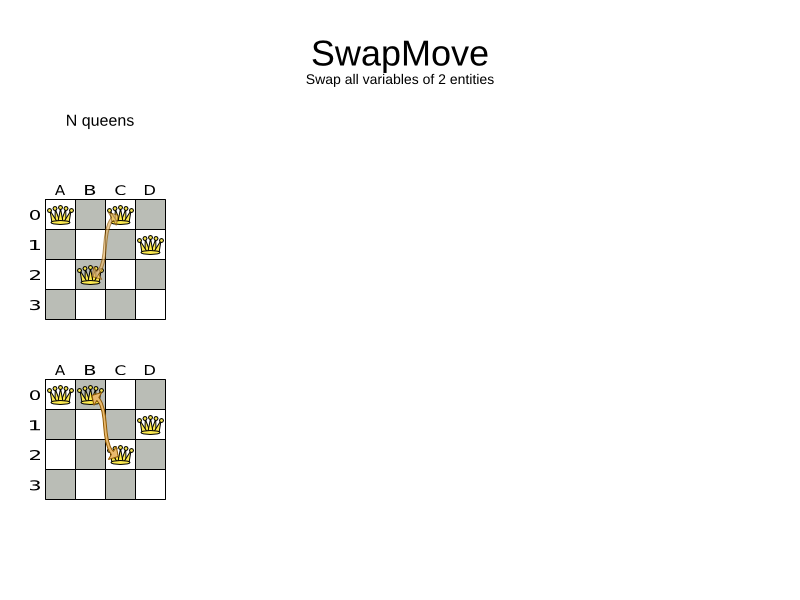
All change moves
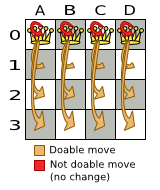
| n | # moves | # solutions |
|---|---|---|
| 4 | 16 | 256 |
| 8 | 64 | 16777216 |
| 64 | 4096 | 10116 |
| n | n2 | nn |
Multiple moves
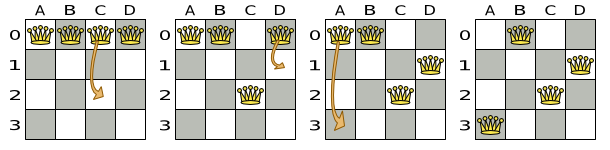
Multiple moves can reach any solution


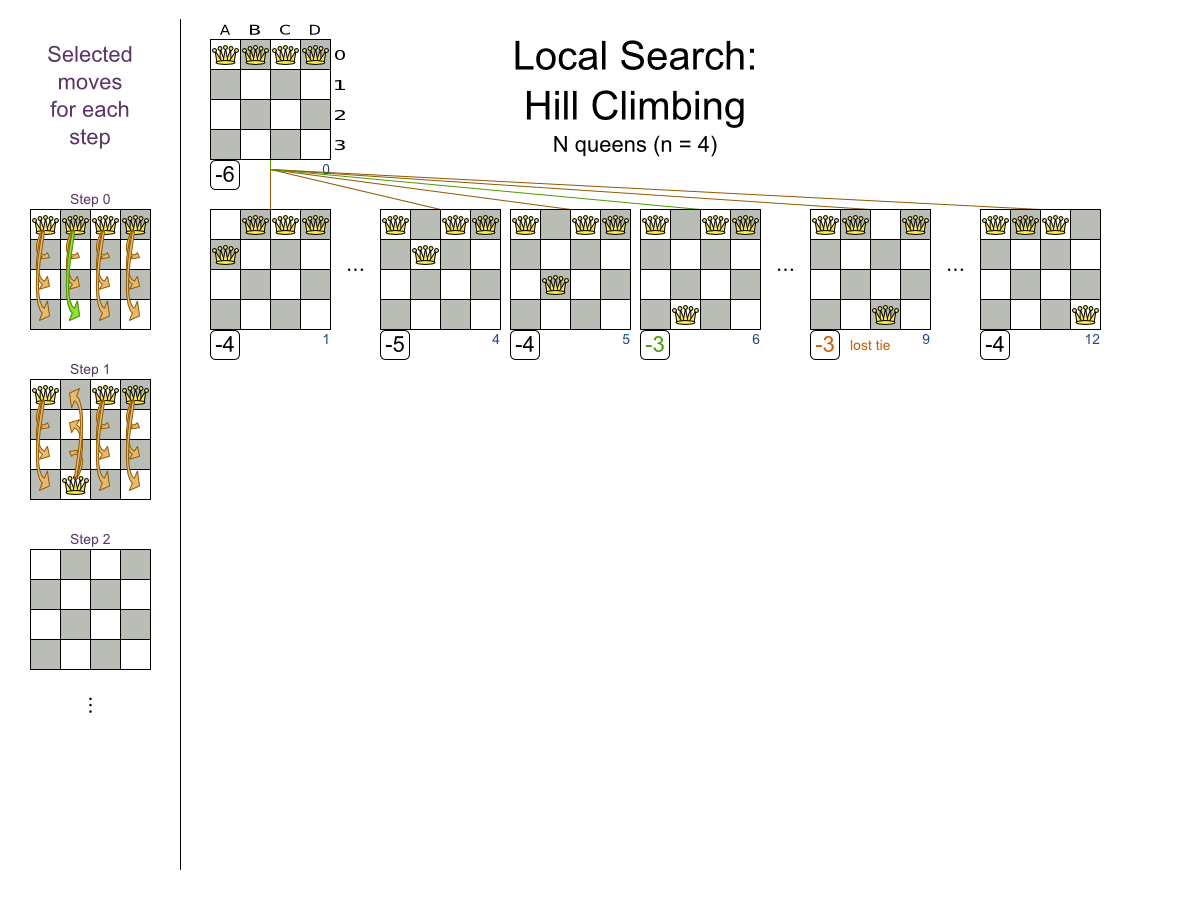
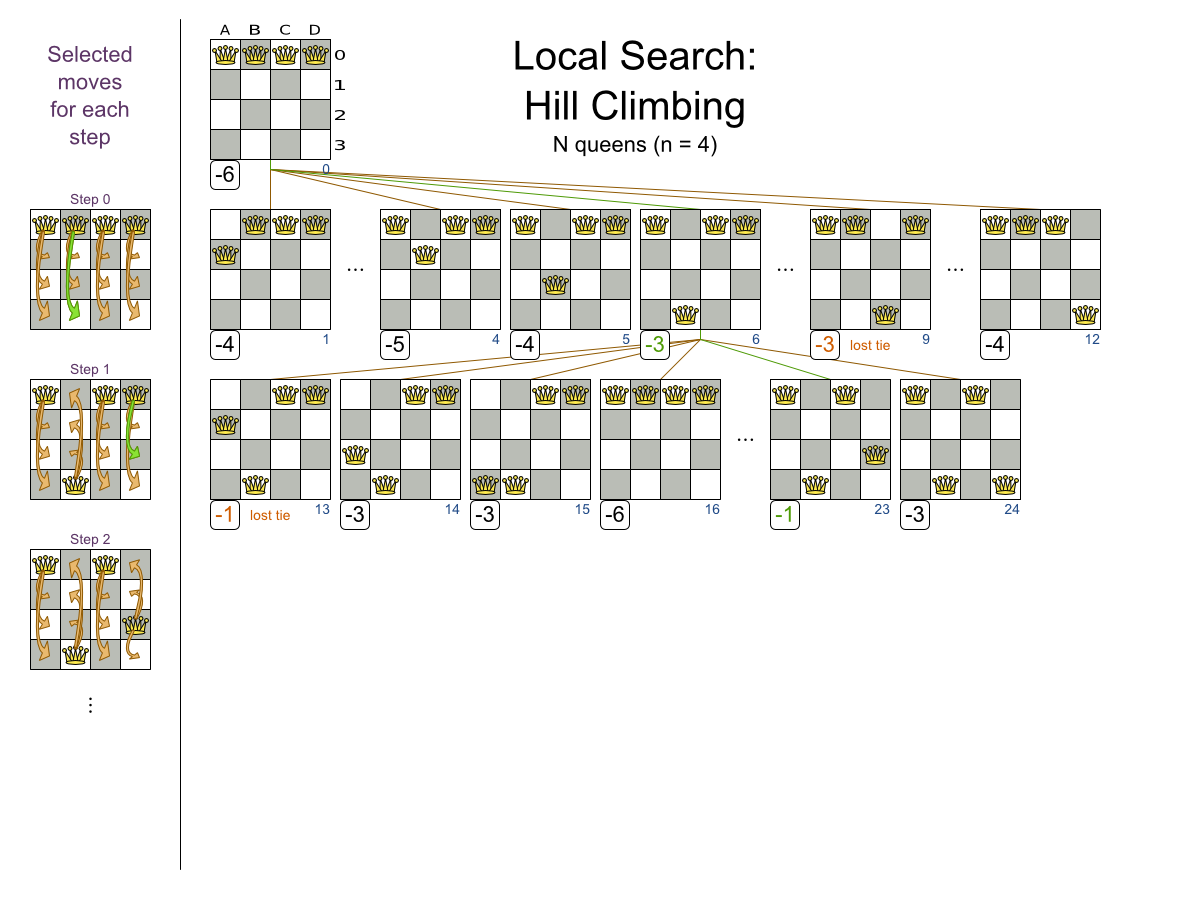


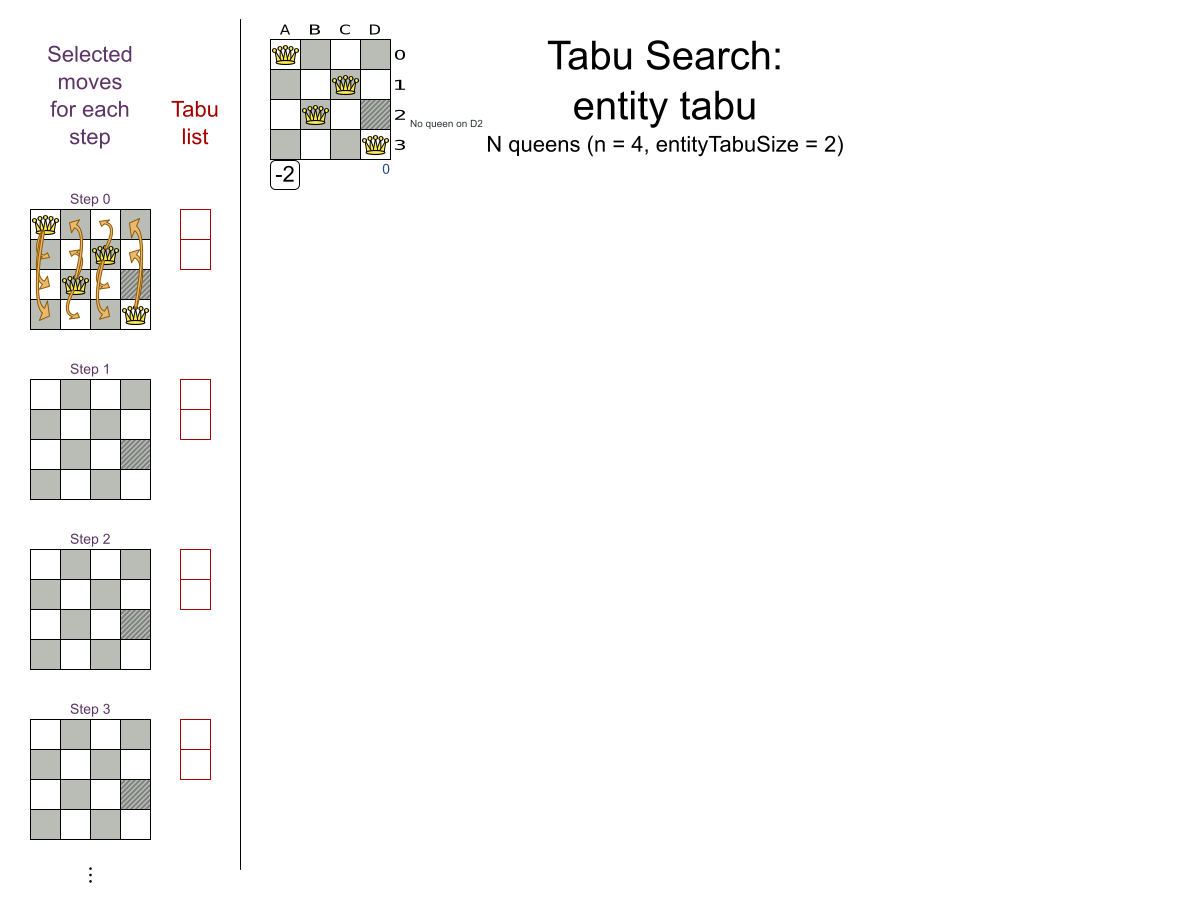
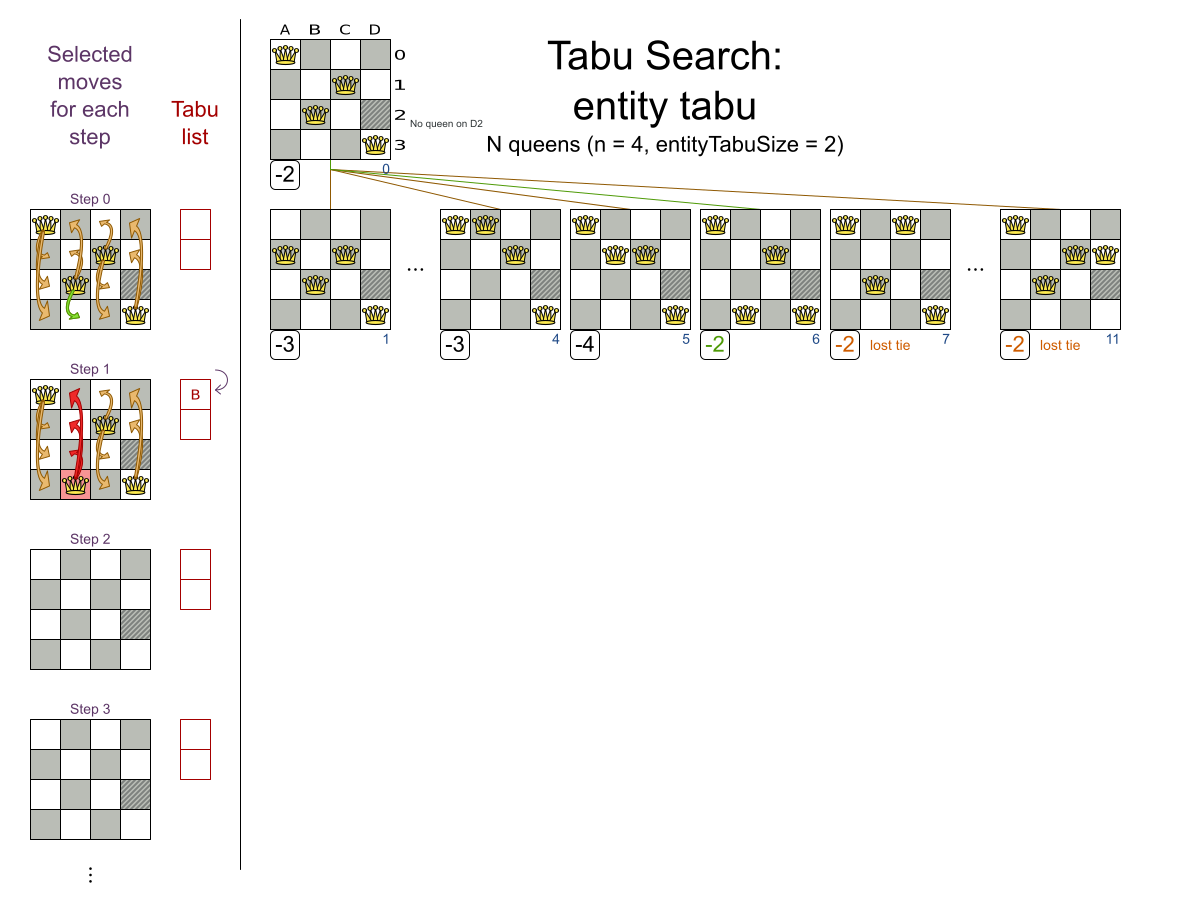
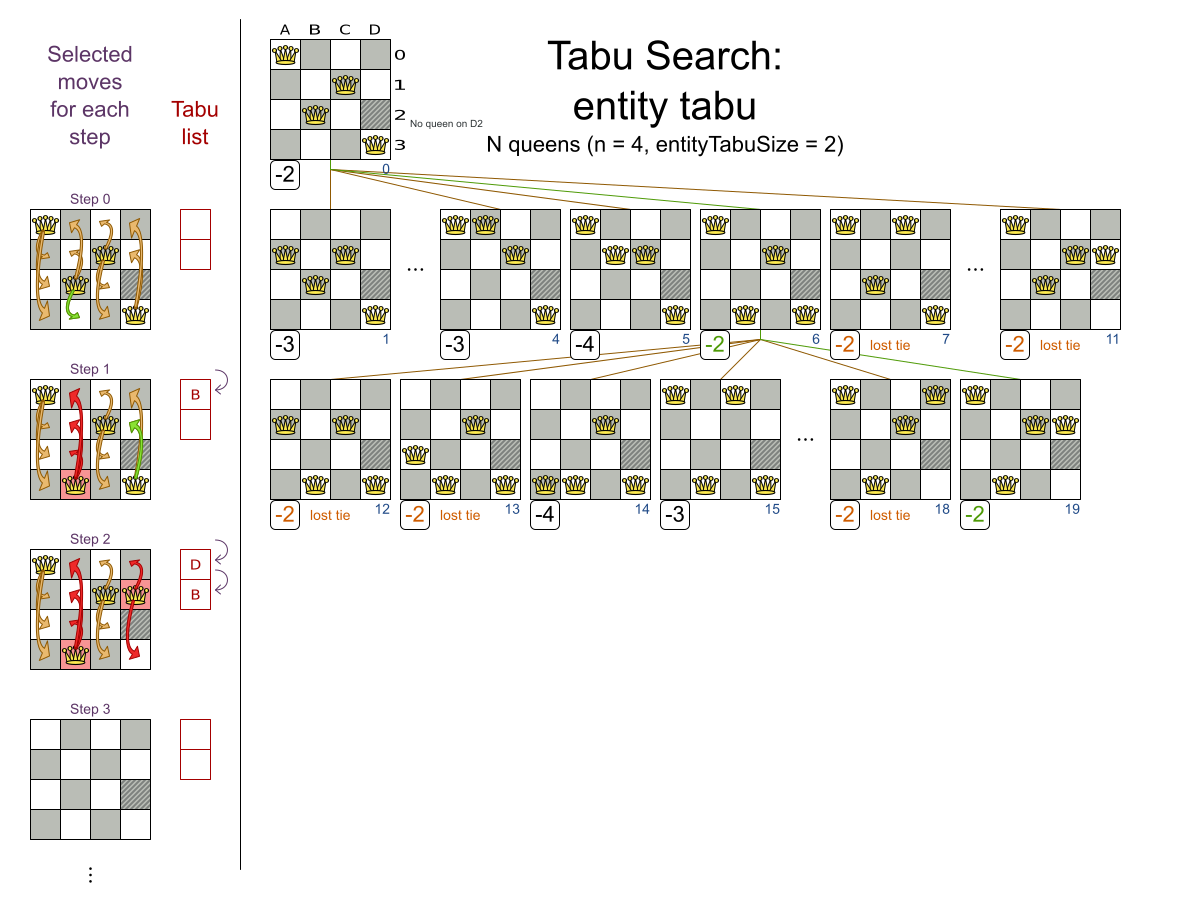
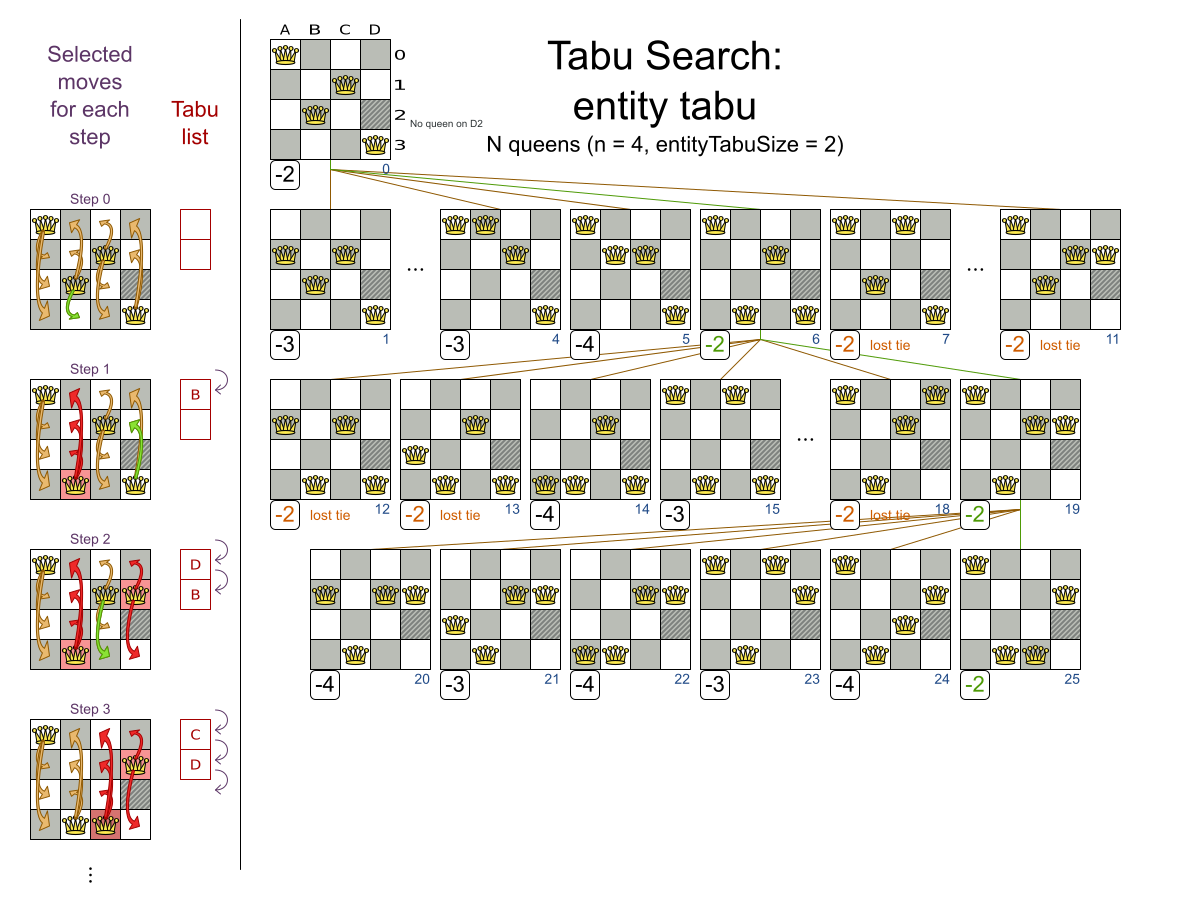

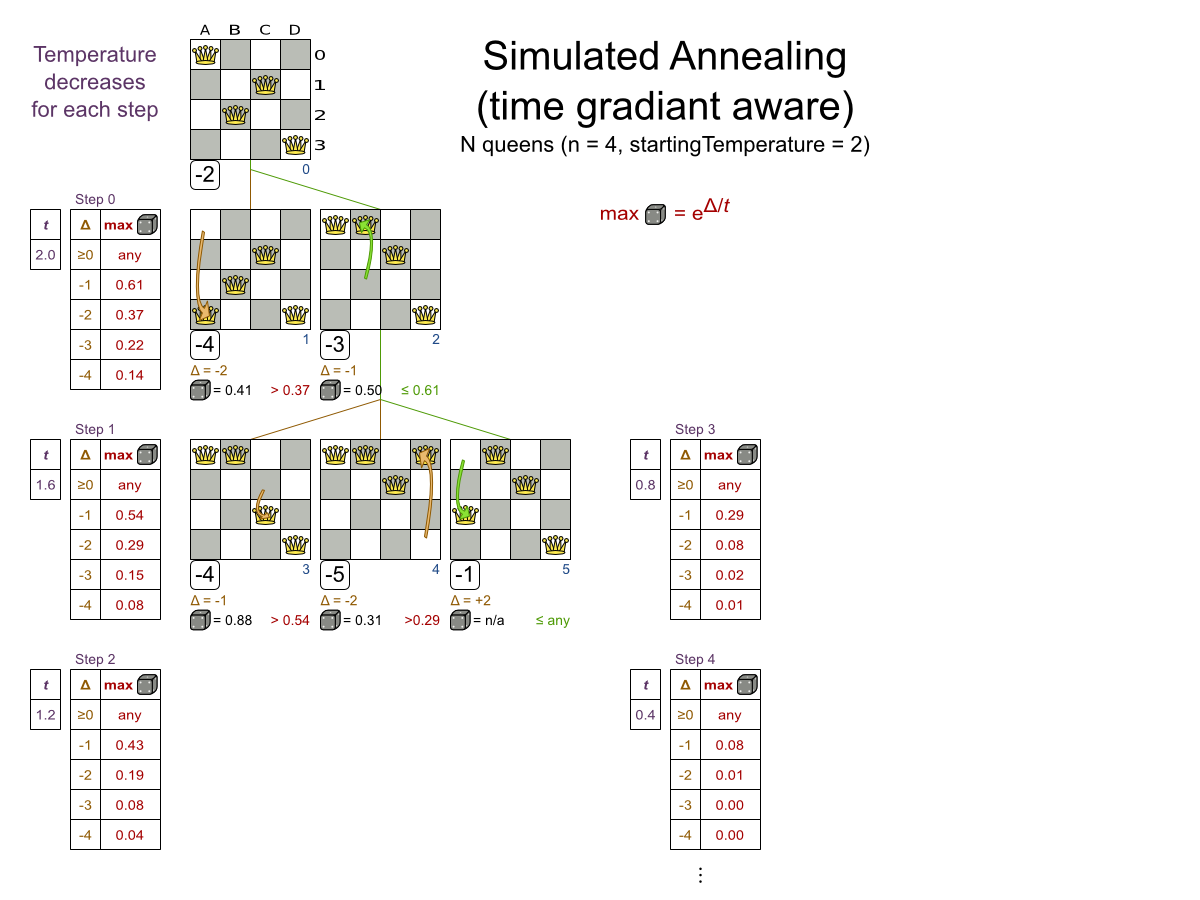
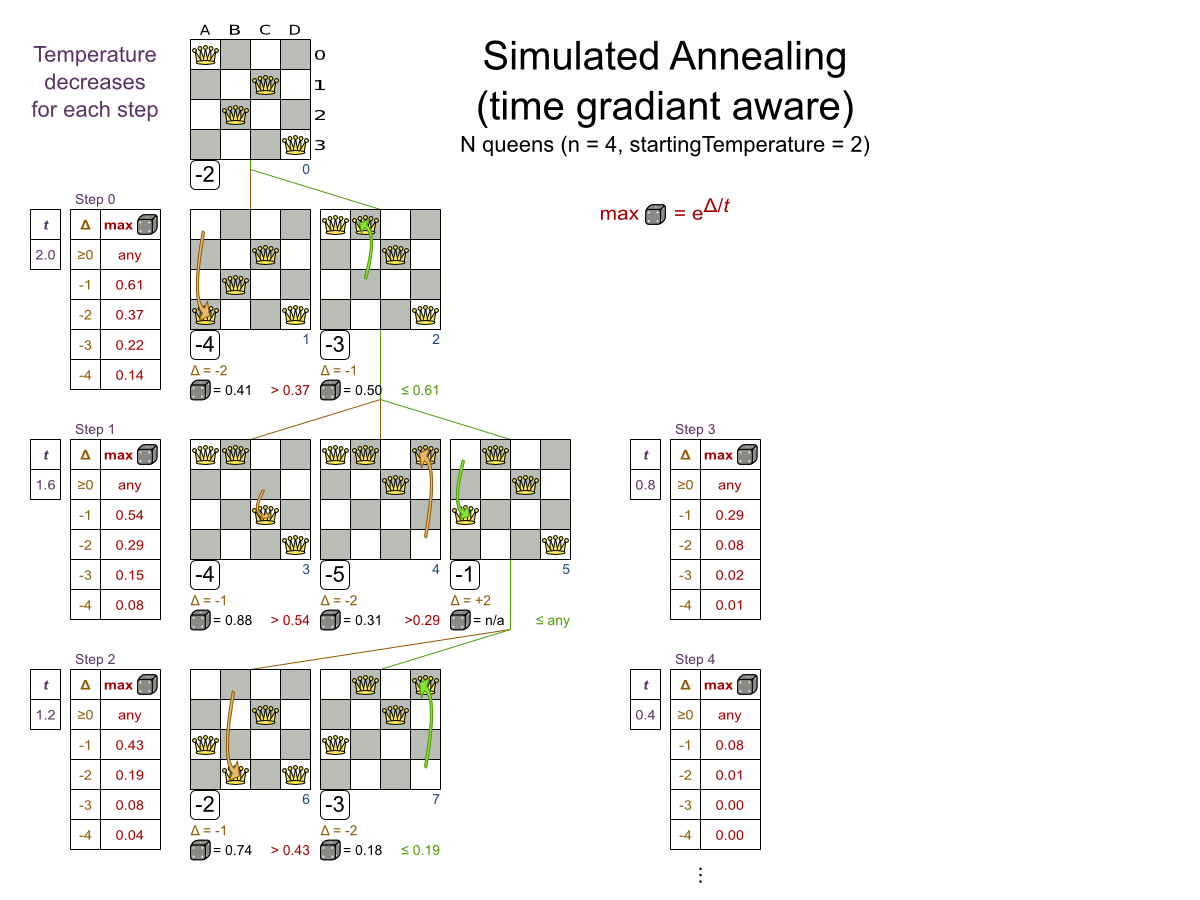
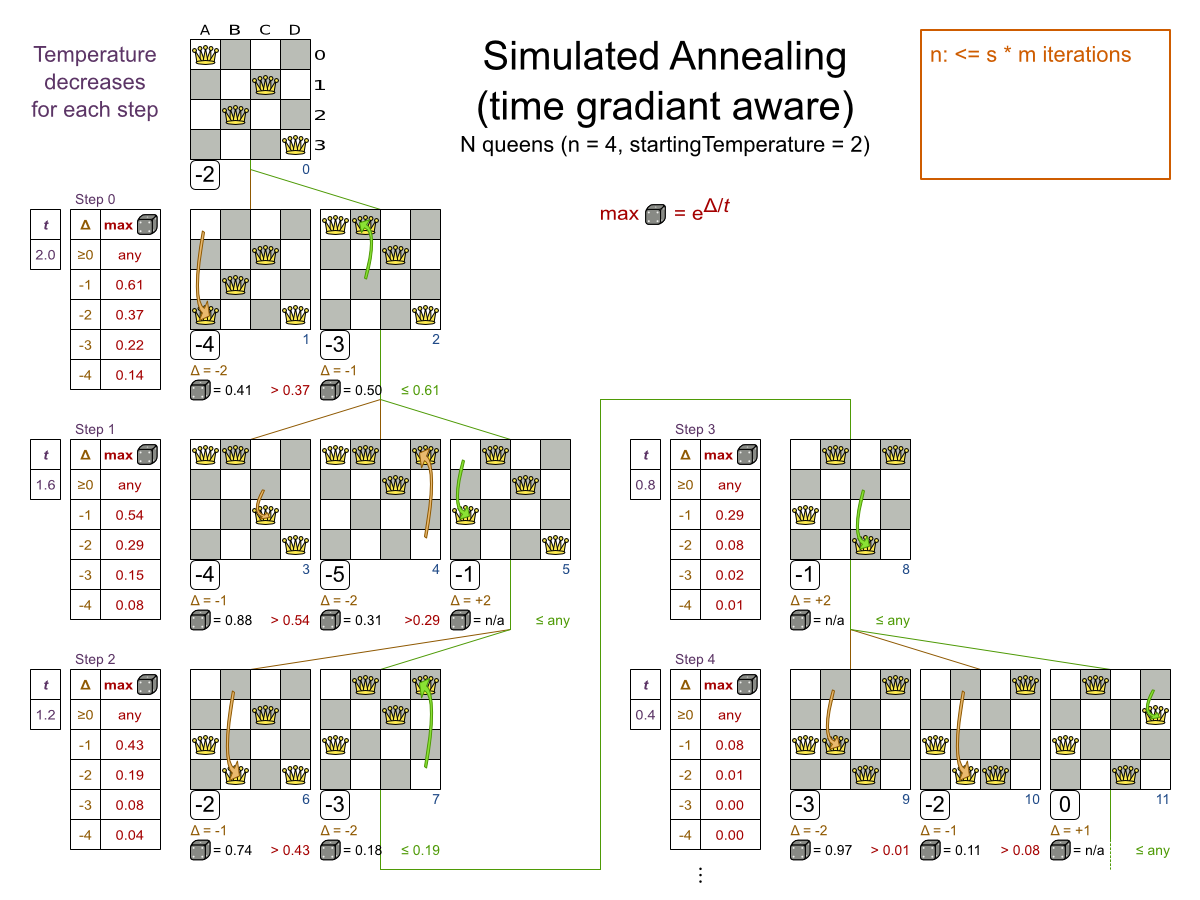


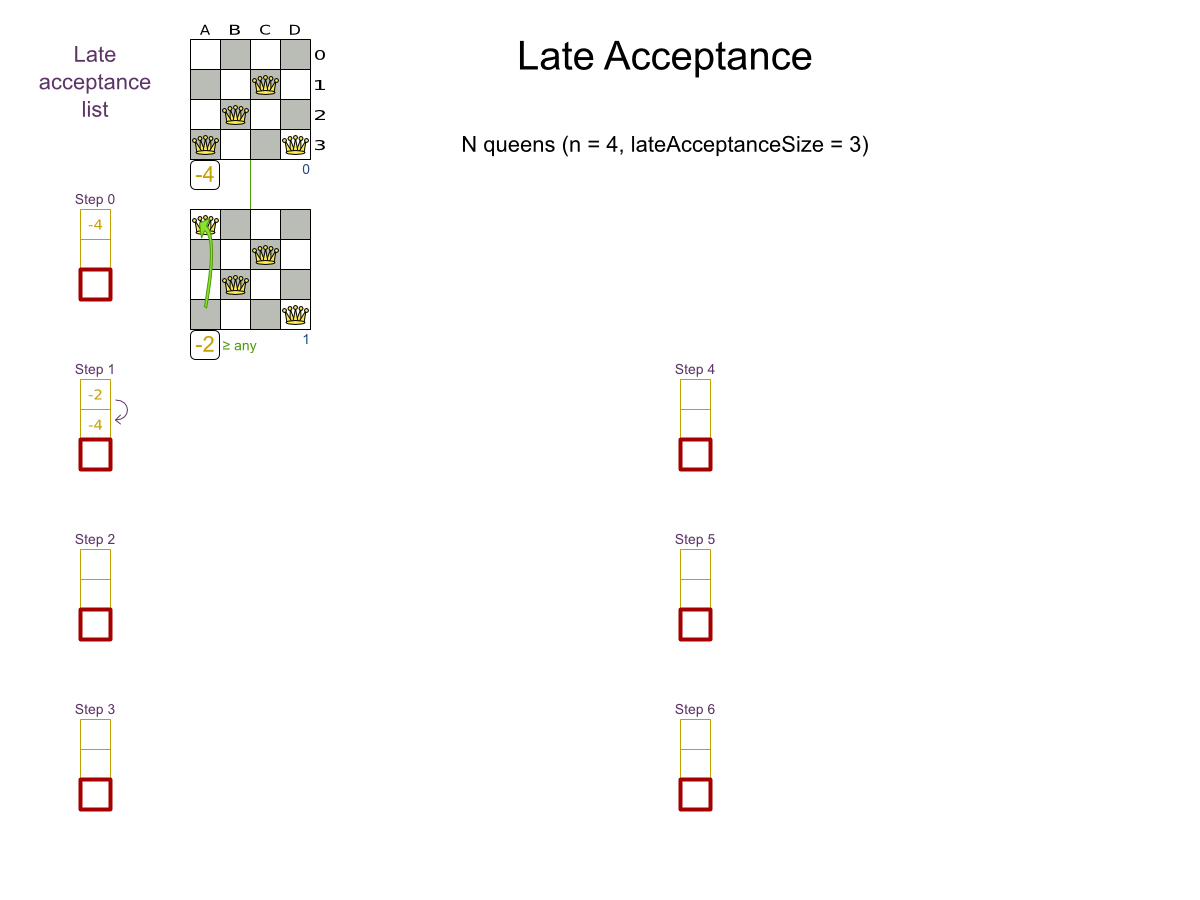

Performance tricks

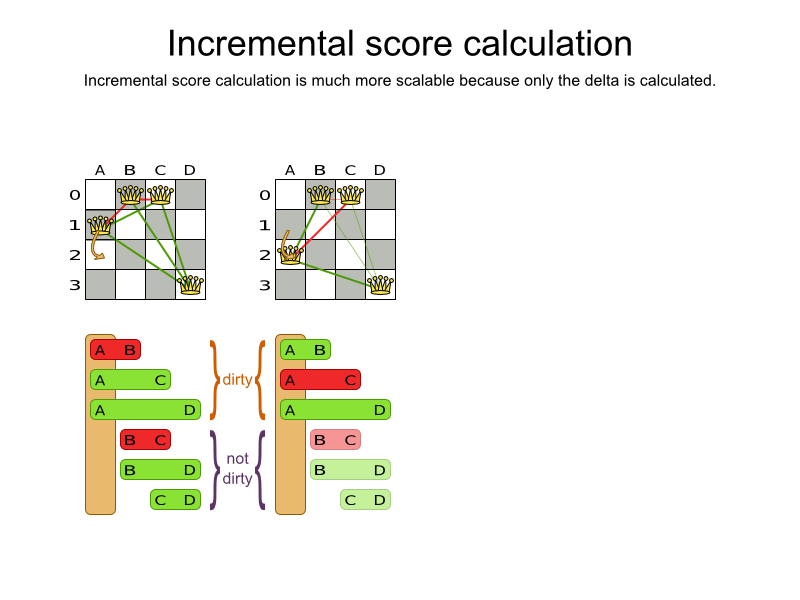
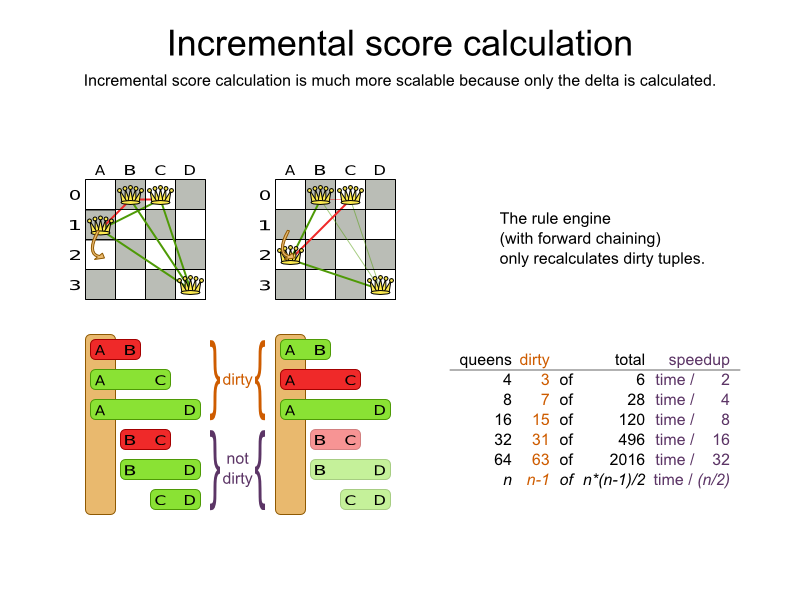
Getting started
Start coding today
- Go to www.optaplanner.org.
- Under the blue button,
click Clone the Quickstarts code. - Run one from source (see README).
For example:
$ git clone https://github.com/kiegroup/optaplanner-quickstarts.git
...
$ cd optaplanner-quickstarts
$ cd use-cases/school-timetabling
$ mvn quarkus:dev
...Q & A
| Homepage | www.optaplanner.org |
|---|---|
| Slides | www.optaplanner.org/learn/slides.html |
| User guide | www.optaplanner.org/learn/documentation.html |
| Feedback |  @GeoffreyDeSmet @GeoffreyDeSmet |